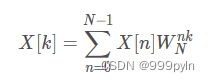在MATLAB中对时域信号进行FFT频谱分析

1.FFT相关知识和MATLAB函数介绍

        · FFT快速傅里叶变换，是将离散的时域信号变换到频域中，一般情况下，时域信号很难看出特征，但是转到频域后，就很容易看出。很多信号都采用FFT，然后对信号进行频谱分析。

        · MATLAB中FFT函数如下：

                                                        Y=fft(X,N);

        · N点FFT变换后，就可以得到N个点的FFT结果。N选取2的整数次方更有利于FFT的计算。

        · FFT公式：

                （1）Xk长度与N相同。应征了上面“N点FFT后，得到N个点的FFT结果”（这N个点，是平铺在0~fs上的，要是只想看前一半，则只是看0~(N/2-1)点）；

                （2）根据奈奎斯特定律，只有fs/2范围内的信号有效可见，所以频谱关于fs/2对称，只看前一半；（应征了上面说的，0~fs对应0点~N-1点。如果只看fs/2以前，除去直流分量，就是只要1~(N/2)这些点）；

                （3）在频谱图上，横轴是f频率，k点的频率为f(k)=k*(fs/N);（k的范围是(0:N-1)，共N个点，根据上述，频谱图上想要只显示fs前一半频率，则k的范围应该是(0:(N/2))，后半部分则是((N/2+1):N-1)这些点）；

                （4）上面提到的fs/N，是频率分辨率，例如如果5Hz、6Hz两信号叠加，他们只相差1Hz。若fs=100，做64点FFT也就是N=64，那么频谱图只能分辨出fs/N=1.56的频率差别，因此频谱图上两信号分辨效果不好。（应改大N值）。然而，对于N的选取，在本文章最后面有一点看法。

                （5）X[0]是直流分量，幅值=模值（X[0]）/N；

                （6）X[k]为k点的频率分量（除X[0]之外），幅值=模值（X[k]）/（N/2）；

2.MATLAB程序

        这个程序建立三个信号，一个低频，两个高频（一个在采样率fs/2 以内，一个超出了fs/2 不符合采样定理）。通过FFT在频域下观察混合信号的特征。分析三个分量的显示情况，分析N的大小对频谱图上的分量频率表示的准确性，分析N和fs的倍数关系对幅值的影响。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%原始信号参数定义
%建立三个信号，一个低频，两个高频（一个在采样率fs/2 以内，一个超出了fs/2 不符合采样定理）
fs=128;				%奈奎斯特采样率=fs/2=64,频率大于64的信号就不能被显示
t=0:1/fs:10;		%创造'时域图'时间序列。时域下信号从0时刻运行到10s时刻，单位时间是1/fs，按1/fs等差序列排列
f1=10;A1=2;			%信号1，频率为10Hz,赋值是2
f2=60;A2=0.5;		%信号2，频率为60Hz,赋值是0.5
f3=68;A3=1;			%信号3，频率为68Hz,赋值是1。不符合采样定理
%%建立正弦信号
s1=A1*sin(2*pi*f1*t);
s2=A2*sin(2*pi*f2*t);
s3=A3*sin(2*pi*f3*t);
s=s1+s2+s3;			%建立混合信号S
%%%作图,图一包含4个时序子图，分别是s1、s2、s3、s
figure(1);
subplot(4,1,1);plot(t,s1,'linewidth',1.5);title('信号s1');xlabel('时间/s');ylabel('振幅');
subplot(4,1,2);plot(t,s2,'linewidth',1.5);title('信号s2');xlabel('时间/s');ylabel('振幅');
subplot(4,1,3);plot(t,s3,'linewidth',1.5);title('信号s3');xlabel('时间/s');ylabel('振幅');
subplot(4,1,4);plot(t,s,'linewidth',1.5);title('信号s');xlabel('时间/s');ylabel('振幅');


%FFT参数定义
N=128;
f=0:fs/N:N-1;					%创造'频谱图'频率序列
%%对混合信号s进行FFT变换
y=fft(s,N);			%对s做N点FFT变换
mag=abs(y);			%模值只要正的
%%%作图，图包含2个子图，分别是完整N点频谱图、只满足采样定理的有用频谱图（常用后者）。
%一定要注意区分'模值'和'幅值'，而且直流分量和频率分量还不一样
figure(2);
subplot(2,1,1);plot(f,mag,'linewidth',1.5);title('完整频谱图');xlabel('频率/Hz');ylabel('模值');	%这是N个点的FFT，0~N-1 对应0~fs
subplot(2,1,2);plot(f(1:(N/2)),mag(1:(N/2))./(N/2),'linewidth',1.5);title('频谱图');xlabel('频率/Hz');ylabel('幅值');	%这是fs/2 之前的频谱，但是要出去f=0 时的直流分量对应1~(N/2)


%完成代码
%%注意，上面一行代码，如果是0~(N/2-1)，那么其中包括了0，也就是包括了直流分量，但是直流分量的‘幅值=模值/(N)’,但是在此也按‘幅值=模值/(N/2)’计算了，这就不对。要注意
%%%通过对照，通常使用的是FFT点减半的‘频谱图’，需要给f、mag都只取前一半(0:(N/2-1))
%%%%通过对照，可以看到一个‘模值’和‘幅值’是不同的，有一个转换关系公式需要添加
%%%%%起始fs=128,N是200，他不是fs的整数倍，‘模值’就会不等于本身模值。只有改成fs的整数倍后，模值才变正常。这就是频谱泄露现象
%%%%%%保持fs=128 不变。N小于128时，如果太小导致‘频率分辨率不足’就会分辨不清楚各个信号分量频率位置，而且幅值也不对有泄露；N越大分量的f值分辨地越清晰
%%%%%%%可以看到，s3不满足采样定理，所以s3不能被显示特征
%%%%%%%%想增粗线条，添加'linewigth',2 ; 想改变点的形状，添加'-x'或'-o'等等形状

        程序很宽，复制到文档里看比较方便。

对于N的选取：

        fs/N是频谱图上的频率分辨率，频率分辨率越高，所能分辨的最小频率差就越小。如一个混合信号中存在5、6Hz，如果fs/N=1，那么可以分辨混合信号中的5Hz和6Hz ；反之，若频率分辨率很小比如fs/N=2，就不能对5、6Hz进行很好的区分，会发生频率的泄露。

        在频率分辨率够用的情况下，不用补0（补0就是N大于采样点个数），如果已知混合信号中需要高分辨率，那么可以增加N提高频率分辨率。但是工程中一般是不知道信号的样子的，所以用下面方式。

        一般情况下，实验中，有多少个采样点就选取N是多少。