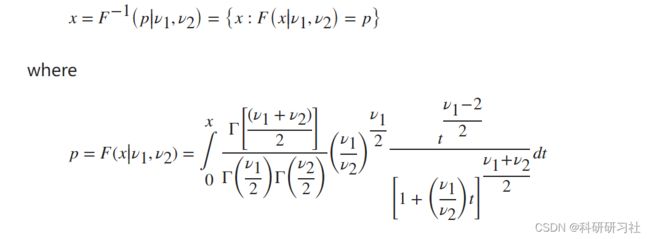【数学建模】单、多因素试验的方差分析(Matlab代码实现)
目录
1 概述
2 单因素方差分析
2.1 语法
2.2 算例 1
2.2.1 算例
2.2.2 Matlab代码
2.2.3 结果
2.3 算例2
2.3.1 算例
2.3.2 Matlab代码
2.4 算例3
2.4.1 算例
2.4.2 Matlab代码
2.4.3 结果
2.5 算例4(不均衡样本)
2.5.1 算例
2.5.2 Matlab代码
2.5.3 结果
3 双因子方差分析
3.1 语法
3.2 算例
3.3 Matlab代码
3.4 结果
4 升级理解
4.1 算例
4.2 Matlab代码实现
4.2.1 写在前面
4.2.2 代码
4.2.3 结果
1 概述
一个复杂的事物,其中往往有许多因素互相制约又互相依存。方差分析的目的是通过数据分析找出对该事物有显著影响的因素,各因素之间的交互作用,以及显著影响因素的最佳水平等。
2 单因素方差分析
Matlab 统计工具箱中单因素方差分析的命令是 anoval 。
若各组数据个数相等,称为均衡数据。若各组数据个数不等,称非均衡数据。
2.1 语法
(1) p=anova1(X)
(2) p=anova1(X,group) %group用于不均衡样本
(3) p=anova1(X,group,displayopt)
(4) [p,table]=anova1(…) %table显示方差表
(5) [p,table,stats]=anova1(…) %stats显示箱图
2.2 算例 1
2.2.1 算例
为考察 5 名工人的劳动生产率是否相同,记录了每人 4 天的产量,并算出其平均值,如表1 。你能从这些数据推断出他们的生产率有无显著差别吗?
| 256 | 254 | 250 | 248 | 236 |
| 242 | 330 | 277 | 280 | 252 |
| 280 | 290 | 230 | 305 | 220 |
| 298 | 295 | 302 | 289 | 252 |
2.2.2 Matlab代码
x=[256 254 250 248 236
242 330 277 280 252
280 290 230 305 220
298 295 302 289 252];
p=anova1(x)
2.2.3 结果
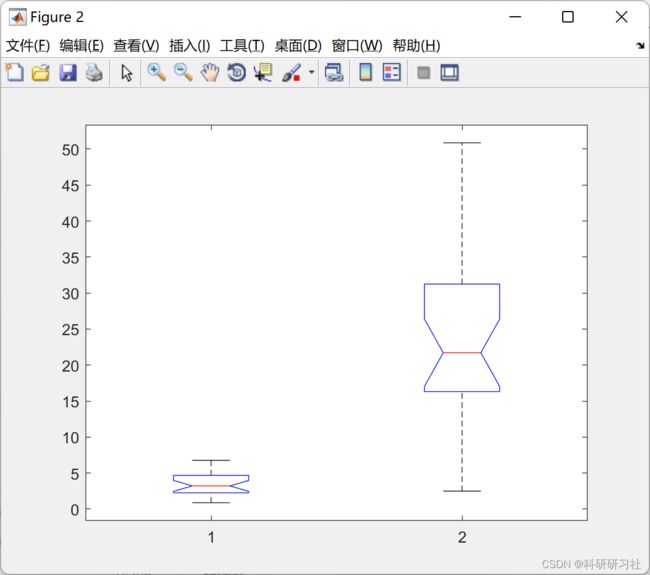
(还输出一个方差表和一个Box图。 )运行后得到一表一图,表是方差分析表(重要);图是各列数据的盒子图,离盒子图中心线较远的对应于较大的F值,较小的概率p.
1)方差表:
anova1函数生成两个图形:
1)第一个图为标准方差分析表,分为六列:
第一列:显示误差来源;
第二列:显示每一误差来源的平方和(ss);
第三列:显示与每一误差来源相关的自由度(df);
第四列:显示均值平方和;
第五列:显示F统计量;
第六列:显示p值.
求得p=0.1109>a=0.05,故接受H0,即5名工人的生产率没有显著差异。若p值接近0,则认为列均值存在差异。若P值小于0.05或0.01,此时拒绝原假设,即5名工人的生产率没有显著差异。
有人要问为什么用结果与0.05来做比较,不然写论文都不会写了,这里普及一下 基本知识:
显著性,又称统计显著性(Statistical significance), 是指零假设为真的情况下拒绝零假设所要承担的风险水平,又叫概率水平,或者显著水平。
显著性的含义是指两个群体的态度之间的任何差异是由于系统因素而不是偶然因素的影响。我们假定控制了可能影响两个群体之间差异的所有其他因素,因此,余下的解释就是我们所推断的因素,而这个因素不能够100%保证,所以有一定的概率值,叫显著性水平(Significant level)。
我们一般认为大于0.05是不显著。显著性大于0.05,证明在百分之五水平上是不显著的。
2)Box图:
2.3 算例2
2.3.1 算例
本算例来源于2022华数杯比赛数据,插层后结构变量、产品性能的变化规律。试验指标就是我们题目中的插层率,因素就是题目中的六个指标(特征)。这里仅以插层率为试验指标,因素就是孔隙率。
2.3.2 Matlab代码
clear all
clc
load data.mat;
p=anova1(data)p = 6.2588e-11<0.05,影响非常显著!
2.4 算例3
2.4.1 算例
例1(均衡样本). 某水产研究所为了比较四种不同配合饲料对鱼的饲喂效果,选取了条件基本相同的鱼20尾,随机分成四组,投喂不同饲料,经一个月试验以后,各组鱼的增重结果列于下表。
四种不同饲料对鱼的增重效果是否显著 ?
| 饲料 | 鱼的增重(xj) | ||||
| A1 | 31.9 | 27.9 | 31.8 | 28.4 | 35.9 |
| A2 | 24.8 | 25.7 | 26.8 | 27.9 | 26.2 |
| A3 | 22.1 | 23.6 | 27.3 | 24.9 | 25.8 |
| A4 | 27 | 30.8 | 29.o | 24.5 | 28.5 |
2.4.2 Matlab代码
A=[31.9 27.9 31.8 28.4 35.9
24.8 25.7 26.8 27.9 26.2
22.1 23.6 27.3 24.9 25.8
]; %原始数据输入
B=A';% 将矩阵转置,Matlab中要求各列为不同水平
p=anova1(B)
2.4.3 结果
因为p=0.0029<0.01,故不同饲料对鱼的增重效果极为显著 .
四种不同饲料对鱼的增重效果极为显著 ,那么哪一种最好呢?请看下图: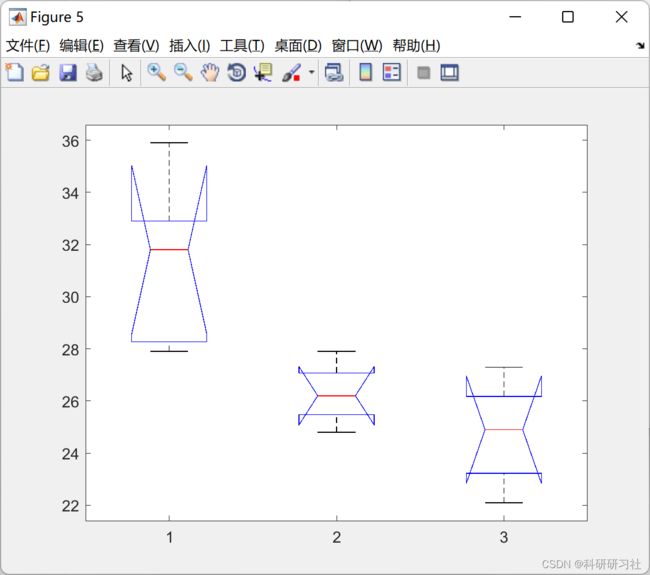
此时,第一个图对应第一种饲料且离盒子图中心线较远,效果最突出。如果从原始数据中去掉第一种饲料的试验数据,得到的结果为各种饲料之间对鱼的增重效果不显著 .
2.5 算例4(不均衡样本)
2.5.1 算例
为比较同一类型的三种不同食谱的营养效果,将19支幼鼠随机分为三组,各采用三种食谱喂养. 12周后测得体重,三种食谱营养效果是否有显著差异?
| 食谱 | 体重增加量 |
| 甲 | 164 190 203 205 206 214 228 257 |
| 乙 | 185 197 201 231 |
| 丙 | 187 212 215 220 248 256 281 |
2.5.2 Matlab代码
A=[164 190 203 205 206 214 228 257 185 197 201 231 187 212 215 220 248 265 281];
group=[ones(1,8),2*ones(1,4),3*ones(1,7)];
p=anova1(A, group)
2.5.3 结果
因为p=0.18630.01,故不同饲料对鱼的增重效果不显著 .
3 双因子方差分析
3.1 语法
双因素方差分析:anova2
调用格式:
(1) p=anova2(X)
(2) p=anova2(X,reps)
(3) p=anova2(X,reps,displayopt)
(4) [p,table]=anova1(…)
(5) [p,table,stats]=anova1(…)其中输入X是一个矩阵;resp表示试验的重复次数输出的p值有三个,分别为各行、各列以及交互作用的概率.
若p<0.05,有显著差异
若p<0.01,有高度显著差异
3.2 算例
为了解3名修理工工作效率,每人修理三种磁盘系统各5个,时间如下:
![]()
3.3 Matlab代码
x=[62 48 63 57 69 57 45 39 54 44 59 53 67 66 47
51 57 45 50 30 61 58 70 66 51 55 58 50 69 49
59 65 55 52 70 58 63 70 53 60 47 56 51 44 50];
p=anova2(x',5);
3.4 结果
单、多因素试验的方差分析
4 升级理解
4.1 算例
银行在国家经济社会发展过程中扮演者重要的决策,银行的破产会对企业和个人造成众多不利的影响。相比国内的银行,国际银行的倒闭频次更高,因此国际银行倒闭原因的分析与预测受到众多管理者与学术研究者的广泛关注。附件1中提供了波兰2017年至2021年的现存或倒闭银行的64项指标数据,各项数据指标具有对应的解释。
请利用该64项指标对银行倒闭的原因进行挖掘,并提供最为重要的5项指标数据及其对应的权重;
4.2 Matlab代码实现
4.2.1 写在前面
X = finv(P,V1,V2)
计算 F cdf 的逆,分子自由度为 V1,分母自由度为 V2,对应于 P 中的概率。P、V1 和 V2 可以是向量、矩阵或多维具有相同大小的数组。标量输入扩展为与其他输入具有相同维度的常量数组。 V1 和 V2 参数必须包含实数正值,并且 P 中的值必须位于区间 [0 1] 内。
F 反函数根据 F cdf 定义为:
从分子为 5 个自由度、分母为 10 个自由度的 F 分布中找出一个应超过 95% 样本的值。
x = finv(0.95,5,10) x = 3.3258 仅在 5% 的时间内偶然观察到大于 3.3258 的值。
4.2.2 代码
clear
clc
load data1.mat;
X=data1(:,3:end);
%% 归一化
X=mapminmax(X',0,1);
group=data1(:,2)';
P=[];
F=[];
Fa=[];
Z=[];
for i=1:size(X,1)
[p,anovatab,stats]=anova1(X(i,:),group);%单因素方差分析
P=[P,p];
fa=finv(0.95,anovatab{2,3},anovatab{3,3});%计算fa
Fa=[Fa,fa];
f=anovatab{2,5};%F值
F=[F,f];
if p<=0.01 & f>fa
Z=[Z,"非常显著"];
elseif p<=0.05 & f>fa
Z=[Z,"显著"];
else
Z=[Z,"不显著"];
end
end
z=find(Z=='非常显著');
P=P(z);
[P,b]=sort(P);
%% top5影响显著的指标
disp('主要指标序号')
a=z(b(1:5));
disp(a)%指标序号
%% 权重就用余弦相似度确定,然后进行归一化
C=[];
for i=1:length(a)
C(i)=(group*X(a(i),:)')/(sqrt(sum(group.^2))*sqrt(sum(X(a(i),:).^2)));
end
W=C./sum(C);
disp('权重')
disp(W)
%% 评价值
P=[data1(:,1:2),X(a,:)'*W'];
%% 检验通过后,接下来就是求分界线,其实就是依次分类统计下均值在取个中间值就好了
%求每个主要指标的
% M=[];
% for i=1:length(a);
% M(i,:)=[mean(X(a(i)),find(data1(:,2)==0)),mean(X(a(i),find(data1(:,2)==1)))];
% end
% disp('主要指标分界点')
% M=mean(M,2)4.2.3 结果
主要指标序号
51 35 16 26 3
权重
0.2367 0.1979 0.1844 0.1857 0.1953