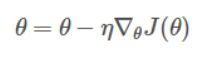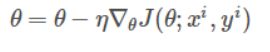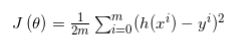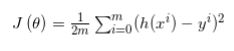机器学习--梯度下降与一元线性回归
目录
梯度下降
基本概念
梯度下降步骤
批量梯度下降(BGD)
随机梯度下降(SGD)
一元线性回归
线性回归概念
原理引入
代价函数
公式推导
代码
一元函数
多元函数
梯度下降
基本概念
梯度下降法,又名最速下降法是求解无约束最优化问题最常用问题的方法,它是一种迭代方法,每一步都是主要的操作目标函数的梯度向量,将当前位置的负梯度方向作为搜索方向。
梯度下降步骤
1、随机初始化函数
2、确定学习率
3、求出损失函数对参数梯度
4、按照公式更新参数
5、重复3,4直到满足终止条件
批量梯度下降(BGD)
批量梯度下降算法(BGD),其需要计算整个训练集的梯度,即:
其中η为学习率,用来控制更新的“力度”/"步长"。
优点:对于凸目标函数、可以保证全局最优,但是对于非凸函数,可以保证一个局部全局最优
缺点:速度慢,数据量大时不可行,无法在线优化
随机梯度下降(SGD)
随机梯度下降算法,仅计算某个样本的梯度,即针对某一个训练样本xi及其yi更新参数
逐步减小学习率,SGD表现得同BGD很相似,收敛效果很不错。
优点:更新频率更快,可以在线优化;一定的随机性导致有几率跳出局部最优
缺点:随机性可能导致收敛复杂化,即使达到最优化仍然会进行过度优化,因此SGD优化过程相比BGD充满动荡
一元线性回归
线性回归概念
回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可以用一条直线近似表示,这种回归分析称为一元线性回归分析;如果回归分析包括两个或者两个已上的自变量,且因变量和自变量是线性关系,则称为多元线性回归方程
一元线性回归方程其实就是从一堆训练集去算出一条直线,使数据集到直线间的距离差最小。
f(x) = ax+b
原理引入
唯一特征x,共有m = 500个数据集,y是实际结果,要从中找到一条直线,使数据集到直线之间的距离差最小,如下图所示: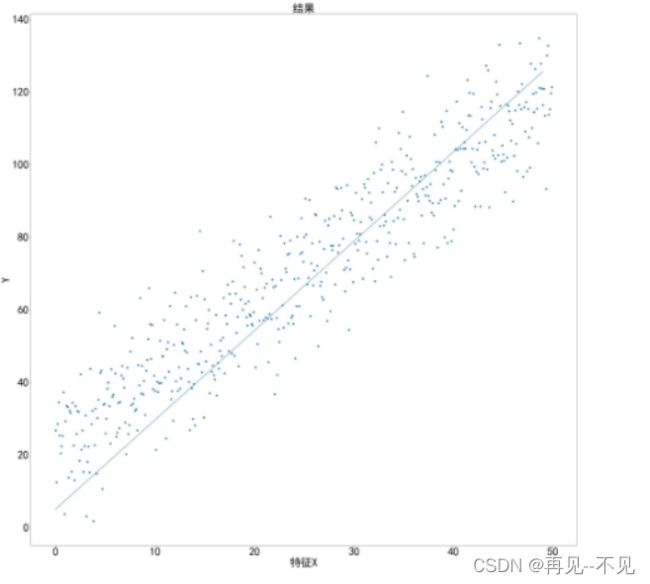
线性回归所提供的思路是,先假设一条直线:
h(x) = a + bx
可以将特征x中每一个x值代入其中,得到对应h(x),定义可将损失定义为y和h(x)之间的差值平方和:
而为了之后计算将其修改为:
接下来求出J的最小值就可
代价函数
公式推导
代码
一元函数
#一元函数
##代码实现 y = 1/2*x*x-2*x+3
import numpy as np
import matplotlib.pyplot as plt
#函数部分
def f(x):
return x**2*0.5 - 2*x + 3
#求导
def d_f(x):
return (x-2)
##定义梯度下降算法
def gradient_descent():
times = 100
alpha = 0.1#学习率
x = 10 #设定x的初始值
x_axis =np.linspace(-10,10)##设定x轴的坐标系
fig = plt.figure(1,figsize=(5,5))#设定画布的大小
ax = fig.add_subplot(1,1,1)##设定画布内只有一个图
ax.set_xlabel('x',front=14)
ax.set_ylabel('y',front=14)
ax.plot(x_axis,f(x_axis))#作图
for i in range(times):
x1 = x
y1 = f(x)
print("第%d次迭代:x = %f,y = %f" % (i+1,x,y1))
x = x - alpha*d_f(x)##更新x
y = f(x) ##更新y
ax.plot([x1,x],[y1,y],'ko',lw = 1,ls = '-',color = 'coral')
plt.show()
if __name__=="__main__":
gradient_descent()多元函数
##多元函数 代码实现
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
##获取f(x)的函数值
def fx(x,y):
return (x-10)**2+(y-10)**2
def d_fx(x,y):
return 2*(x-10)
def d_fy(x,y):
return 2*(y-10)
def gradient_descent():
times = 100##迭代次数
alpha = 0.1 ##学习率
x = 20#x的初始值
y = 20#y的初始值
##绘图操作
fig = Axes3D(plt.figure()) ##将画布设置为3D
axis_x = np.linspace(0,20,100)
axis_y = np.linspace(0,20,100)##设置x,y的取值范围
axis_x,axis_y = np.meshgrid(axis_x,axis_y)##将数据转变为网格模式
z = fx(axis_x,axis_y)##计算z轴的值
fig.set_xlabel('X')
fig.set_ylabel("Y")
fig.set_zlabel("Z")
fig.view_init(elev=60,azim=300)##设置为3D得到俯视角度 方便查看梯度下降曲线
fig.plot_surface(axis_x,axis_y,z,rstride = 1,cstride=1,cmap= plt.get_cmap('rainbow'))##做出底图
###计算极值
for i in range(times):
x1 = x
y1 = y
f1 = fx(x,y)
print("第%d次迭代: x=%f,y=%f,f = %f"%(i+1,x1,y1,f1))
##对x,y进行更新
x = x - alpha*2*d_fx(x,y)
y = y - alpha*2*d_fy(x,y)
f = fx(x,y)##更新f
fig.plot([x1,x],[y1,y],[f1,f],'ko',lw = 2,ls='-')##绘制点
plt.show()
if __name__ == "__main__":
gradient_descent()