辣鸡准备稍微碰一下深度学习系列(1/21)---上

前BB

  大学三年，啥都没会。
  吃饭第一，睡觉不愧。
  进入好班，向大佬跪。
  找个导师，方向血亏。
  未来迷茫，欲极东飞。
  研究不明，被教授怼。
  论文全英，头颅要坠。
  早知今日，专业选对。

  买了本《21个项目玩转深度学习》，立个把上面21个全部搞懂的flag，并发在这100%没人看我帖子的csdn上，进行自我麻痹，完美。

MNIST数据集

一、是啥玩意？

  Mixed National Institute of Standards and Technology database(MNIST)是个手写数字二值图像数据库，有0~9,10种阿拉伯数字。其中训练集有60k张，测试集10k张，每张图片大小为28px x 28px，并配有标签，标注该手写数字数值。

二、怎么得到？

  由于本辣鸡开始重新做人学东西的时候重新更新了所有库，导致tensorflow到了2.3.0版本，非常完美得将1.0时期得获得方法（用tutorials包下载,重新把它下回来也行）干掉了。めでたしめでたし。

第一种：找大腿（keras）

  这位上层API接口大腿封装了一堆东西，例如下载MNIST数据库。如下代码实现用keras下载MNIST数据库。从这里学到的，除了CtrlCV就不会干别的了。

import tensorflow as tf # 上大哥

mint = tf.keras.datasets.mnist # 抱大腿
(x_train,y_train),(x_test,y_test) = mint.load_data() # 让大佬帮忙装下数据

第二种：伸手要

讨要过程

  代码不给下那么自己找，网上各位大佬给的各种地方都可以下MNIST，但时代变迁各种地址可能会有变化，但好像这里是官网http://yann.lecun.com/exdb/mnist/。并且还附赠各种分类策略的错误率一览，非常perfect，可以给自己的代码一个“你这错误率怎么跟他正确率一个水平？”的忠告。
  该文件类型为idx3-ubyte（image）和idx1-ubyte（label），这玩意好比八百米火腿肠，直接把所有东西弄成一大串字符集合扔给你，自己切去hhh。
  对于idx3-ubyte（image）这条火腿肠。直接print（切片了头部分字符）后长这德行。

b"\x00\x00\x08\x03\x00\x00\xea`\x00\x00\x00\x1c\x00\x00\x00\x1c\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x03\x12\x12\x12~\x88

  蓝色的0083是magic number，指的是描述程序或数据的常数。这里的0083中，8指的是8位一字节,每个字节代表一个无符号数，3指的是三维数据（灰度图二维 X 一群图片 = 三维）。
  红色\x00\x00\xea`指的是图片个数60000，其中\xea十进制为234，‘的ascii码为\x60十进制为96，则234x16^2+96=60000。
  绿色为图片大小（高和宽）都是28。
  之后灰色就一直是灰度值了，对应如下。所以知道这些常数，就可以从第（4+4+8+1）=17个字开始28x28个一切，切60000次就能把图像切出来。

0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 18, 18, 18, 126, 136

  对于idx1-ubyte（label）的情况，magic number是0081（1是一维，一串标签），大小也是\x00\x00\xea`，之后就是标签的数值了。所以从（4+4+1）=9个子开始一个一个切。

处理过程

  拿到了数据后就可以直接找切肉的（struct）帮忙切开。屠夫使用方法与加工方法一览

import struct # 切肉的

with open('MNIST_data/train-images.idx3-ubyte','rb') as f:
    image = f.read() # 读训练图
with open('MNIST_data/train-labels.idx1-ubyte', 'rb') as f:
    labels = f.read() # 读训练标签
    
x_train = []
'''
struct.calcsize() 方法输入参数（fmt），返回calculate了fmt的size（int）
fmt(format)为格式字符串，其中第一位代表字节顺序等信息（ > 代表高位编址，标准大小），
之后代表格式字符（I为unsigned int，四个I分别代表1个magic number,1个图片个数，2个图片大小）
一个unsigned int为4个标准大小，计算出来应该是4个标准大小为16，所以直接把index赋值为16就ok
'''
index = struct.calcsize('>IIII') # index = 16

# 切图片
for i in range(60000): # 知道有多少图像就懒得拆出来图像个数大小了
    # 从第17位开始以784个byte（1个标准大小）来unpack image这个火腿肠
    temp = struct.unpack_from('>784B', image, index) 
    # 添加把一段小火腿肠reshapecheng图像的二维大小
    x_train.append(np.reshape(temp, (28, 28))) 
    
    index += struct.calcsize('>784B') # index += 784 坐标后移784各标准大小，下一张

#切标签
y_train = []
index = struct.calcsize('>II') # index = 8
for i in range(60000):
    temp = struct.unpack_from('>1B', buf, index)
    l.append(temp[0]) # 由于切出来是个1维数组，就要里面的东西就行
    index += struct.calcsize('>1B') # index += 1

  朋友说有轮子了为啥要自己造轮子hhh。有keras这个大腿非得要这么用，也就是我这死心眼这么执着了hhh。可巧，我硬想要输出一下所有图片的灰度值数组，由于我用的jupyter notebook，于是出现了新问题。

  啊哈，不让我接着输出了，这还要限制输出率，这玩意得治一治。从这里学到了解决办法。在cmd里把jupyter的各种设置召唤出来，进行魔改就ok。
  于是 fatal error C1083: 无法打开包括文件: “io.h”: No such file or directory 这位老哥就出来了。这玩意召唤还得要C语言头文件魔法阵还不成？这里说怎么找到魔法阵。只要把windows sdk魔法阵集下下来，啥魔法阵都可以随便用。
  再次召唤成功就OK了，中途可能还差sys/un.h这位老哥，那就是单纯没设置好anaconda的环境变量了（虽然我用的是miniconda 手动狗头）。再次召唤进行修改就OK了。

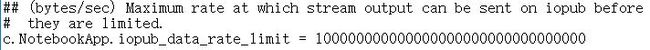
人民站起来了！虽然人民站起来了，但是人民的生活水平收到了影响。结论，没事别在jupyter notebook上print那么长的数据，容易崩hhh。

第三种：自食其力

  只要功夫深，铁杵磨成针，70k个（28px x 28px）的数据，就不信我这辈子做不出来自己的数据集（手动狗头）

结论：keras NB！

三、怎么使用？

  之后直接用keras下载的mnist了。其结构为训练集60k张图像，测试集10k张图像，可以直接将标签信息转为独热编码。所以就照着哪个方向把数据集弄一弄。

1.分验证集

  不知道tutorials的验证集怎么分的，我就把后10%当成验证集了hhh。

x_valid = x_train[55000:]
y_valid = y_train[55000:]
x_train = x_train[:55000]
y_train = y_train[:55000]

2.标签换成独热编码

  没记错的话独热编码（one-hot）顾名思义，只有东京特别热？让一串0中间出来一个陈独秀1。由于真实标签中没有大小关系的意义，就是谁是1，谁是4，跟谁是苍老师，谁是新人一个类型，即离散的。所以其作用主要是破坏出现在标签中的大小关系，让所有标签对任何其他标签都是平等的（距离相等）。并且还能减少训练时候，数字大小带来的影响，虽然1和9可能影响不大，但1和1000就出来了。当时可能是看的这个。

Y = np.hstack((y_train,y_valid)) # 这句话被称为吃饱了撑的没事干
Y = np.hstack((Y,y_test)) # 跟上句一样统一处理

Y_onehot = np.zeros((70000,10))
index = 0 # 一维坐标
for i in range(70000): # Y[i]为陈独秀的位置
    Y_onehot[index,Y[i]] = 1
    index += 1

  然后再把弄好的独热标签分开就ok。这里有更高级的方法。

3.最后样子

print(x_train.shape) # (55000, 28, 28)
print(y_train.shape) # (55000, 10)
print(x_valid.shape) # (5000, 28, 28)
print(y_valid.shape) # (5000, 10)
print(x_test.shape) # (10000, 28, 28)
print(y_test.shape) # (10000, 10)

叫上大哥拿家伙开练

一、Softmax回归

1.Softmax回归部分原理

  Softmax回归是逻辑回归（二分类）的升级版（多分类）。
  其中逻辑回归计算的是正负类两人的概率，通过某sigmoid函数（h(w,b;x)），将算完的数映射0还是1（负类还是正类）。sigmoid函数又可以求导，又可以把数尽可能弄到0或者是1，优秀。

$$h(w,b;x)=\frac{1}{1+e^{(-w^T\cdot x+b)}}$$
  算着这玩意找和真实标签值最近的函数，求极大似然函数来解决代价函数的定义，然后请出牛顿或者梯度下降来求极大似然函数的梯度，然后一步一步似爪牙一般改变w向量和b向量的值让代价函数往极值点靠，到一定程度就可以收手交工了。
  多分类的话就没有正负类这一说了，得大家一起评评理，认哪个亲。也就是说，根据w和b对X进行评理，要算出来各位分到不同的类别的概率为多少，找到最大概率的那一位。当然概率在0到1之间且和为1这件事说明，函数不仅跟指数e有不解之缘，并且还得归一化。
  在二分类中一个概率计算完了后，用1减一下它就是另一种的概率，咱多分类使不得，直接设w矩阵（样本属性个数 x 分类种数），b向量（分类种数 x 1），然后直接对应计算哪一个标签概率，就用哪一列w和哪一个b。
  比如瞎编的x，b，w如下所示，样本属性有4个，分3个标签，w矩阵大小就应该是4x3，b向量为3x1。先忽略训练数据归一化等麻烦事，先分别计算它们的概率。
$$x=[1,2,3,2{]}^{T}w=\left[\begin{array}{ccc}1& -2& 2\\ 1& 0& -1\\ 2& 1& 0\\ -1& 1& -1\end{array}\right]b=[-1,2,1{]}^T$$
  除了我的报告不在最后一个时间点上交的概率为-100%之外就没有负的概率了。w${}_0$${}^T$为w的转置后的第一行（第一列的转置）
$$\begin{gathered} e^{w_0^{T}x+b_0}=e^{1\cdot 1+2\cdot 1+3\cdot 2+2\cdot (-1)+(-1)}=403.4 \\ {e}^{w_1^{T}x+b_1}=148.4 \\ {e}^{w_2^{T}x+b_2}=0.4 \end{gathered}$$
  归一化获得概率
$$\begin{gathered} P\{y=0|X\}=\frac{403.4}{403.4+148.4+0.4}=0.7305 \\ P\{y=1|X\}=\frac{148.4}{552.2}=0.2687 \\ P\{y=1|X\}=\frac{0.4}{552.2}=0.0008 \end{gathered}$$
  得知这位x要归到y=0。总结成公式为
$$p_y=softmax(w^T\cdot x+b{)}_y=\frac{e^{w_y^T\cdot x+b_y}}{\sum _{i=0}^n{e}^{w_i^T\cdot x+b_i}}$$
  继续极大似然函数后定义评价函数，然后就是公式的一系列捣鼓了，反正tensorflow大哥帮着算，小弟我就直接空手套白狼了（手动滑稽）。

2.大哥风光

  由于softmax中间节点对输入节点无物理性质全连接，所以需要把28px x 28px的图转成784个属性来操作。其次对于如此庞大的数据，归一化一下，防止某些200以上的老哥独领风骚。这次大方的用了float64数据类型hhh。大佬太多真爽。

x_train = tf.cast(x_train,tf.float64)/255
x_train = tf.reshape(x_train,(55000,784))

x_valid = tf.cast(x_valid,tf.float64)/255
x_valid = tf.reshape(x_valid,(5000,784))

x_test = tf.cast(x_test,tf.float64)/255
x_test = tf.reshape(x_test,(10000,784))
#虽然放一起一块转也行，但懒得弄了

  之后大哥就该登场了

import tensorflow as tf # 给足大哥场面
import numpy as np

# tf.Variable初始化变量函数，W矩阵大小（784,10）随机数，平均0，标准偏差0.01，需要与x矩阵同数据类型
W = tf.Variable(tf.random.normal(shape=(784, 10)
                                 , mean=0
                                 , stddev=0.01
                                 , dtype=tf.float64))
# b向量初始全为0，数据类型一致
b = tf.Variable(tf.zeros(10, dtype=tf.float64))

  这次由于数据较多，有几种不同梯度下降方式，一般方法都分三种，特别左，特别右和适当，分别对应这些名字。虽各有利弊，但做一个普通人就挺好。所以选择了小批量迭代梯度下降。要是用保守的批量梯度下降法，我这里分分钟计算出nan出来，直接干出天文数字hhh。

def acc(x,y,n):
    z = tf.matmul(x,W) + b
    soft = tf.exp(z)/tf.reduce_sum(tf.exp(z),axis=1, keepdims = True)
     # 没存数值标签，懒得回去弄了hhh，直接找独热码的index和softmax的index的差异
    diff = tf.argmax(soft,axis=1) - tf.argmax(y,axis=1)
    # 换成list，不然没法用count（）函数
    diff = list(diff)
    # 没差异就对了，有差异就错了
    return diff.count(0)/n


learn_rate = 0.001 # 悠着点
batch_size = 500 # 500一组
epoch = 10 # 来10代（虽然不用那么多）

for i in range(epoch):
	# 将这个tensor给slice成batch_size大小的train_iteration
    train_iter = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(batch_size)
    for X,Y in train_iter:
        with tf.GradientTape() as tape:
        	# 先算logit (tf.mat_multiply(mat1,mat2))
            Z = tf.matmul(X,W) + b
            #然后算softmax tf.reduce_sum() 降维求和。
            '''
            Z这个tensor是二维的，如果设定只按行求和（axis=1），形成分母，去同行一起除除一个二维的tensor，
            需要形成一个1列的二维tensor，即keep住dimension，而不是一维列向量。
            若是后者，除法会将列向量的长度和Z的行的长度广播到一起，计算错误，前者才是按行相除。
           	广播不到一起，则会报这个错误 Incompatible shapes: [3,4] vs. [3] [Op:RealDiv]
			ps：数字瞎设的
            '''
            softmax = tf.exp(Z)/tf.reduce_sum(tf.exp(Z),axis=1,keepdims=True)
            # 再找对应标签下的概率大小 （tf.boolean_mask 即bool样式的mask，不是true和false也ok（废话hhh）手动@java）
            y_pre = tf.boolean_mask(softmax,Y)
            # 对这堆概率极大似然估计
            L = tf.reduce_sum(-tf.math.log(y_pre))
        # 大哥计算在现在的w和b，Loss对其的梯度
        grads = tape.gradient(L,[W,b])
        W.assign_sub(learn_rate * grads[0])
        b.assign_sub(learn_rate * grads[1])
    if((i+1) % 5 == 0): # 每5代验证一下，虽然没啥乱用。
        print("第%s代：loss:%s;train:%s;valid:%s"%(i+1,float(L),acc(x_train,y_train,55000),acc(x_valid,y_valid,5000)))
    else:
        print("第%s代：loss:%s;train:%s"%(i+1,float(L),acc(x_train,y_train,55000)))

#最后准确率        
print("test:%s"%(acc(x_test,y_test,10000)))

  最后迭代的损失函数和准确率们结果如下。

第1代：loss:208.3210754565345;train:0.8934181818181818
第2代：loss:186.93453085177208;train:0.9034363636363636
第3代：loss:177.13430146437088;train:0.9089090909090909
第4代：loss:171.06870342990425;train:0.9120363636363636
第5代：loss:166.77142519230188;train:0.9146181818181818;valid:0.9322
第6代：loss:163.475600714839;train:0.9163272727272728
第7代：loss:160.81347328777352;train:0.9174727272727272
第8代：loss:158.5850942092462;train:0.9187272727272727
第9代：loss:156.67171705994275;train:0.9195272727272727
第10代：loss:154.99786389996373;train:0.9202181818181818;valid:0.9368
test:0.9217

  由于迭代次数有点多，准确率比书上的91.85%稍微高那么1微米。算是辣鸡的一点挣扎了hhh。

3.大腿真香

  网络上看到王某某的动图，我就算用tensorflow1.x，用pytorch，也不会用你一点keras。---------真香。感觉有点长了，分P吧（手动笑哭）
P2地址：辣鸡准备稍微碰一下深度学习系列(1/21)—下

不能称为reference的reference们
1、Tensorflow 2.0 !!! No module named 'tensorflow.examples.tutorials’解决办法，有用
2、THE MNIST DATABASE of handwritten digits
3、7.3. struct — Interpret strings as packed binary data
4、处理Jupyter Notebook报错：IOPub data rate exceeded
5、pip安装时 fatal error C1083: 无法打开包括文件: “io.h”: No such file or directory
6、为什么要使用独热编码
7、标签转换为独热码的三种方法Python
8、用 TensorFlow2.0 实现 Softmax 多分类
9、深度学习中的三种梯度下降方式：批量（batch），随机（stochastic），小批量（mini-batch）
.