R语言自学笔记：数据处理、数据分布及数据检验

一. 基本的数据统计处理

1. 数据的展示

对于一组数据，可以有许多统计分析的方法。

(1) 基本信息

mean()：求平均值

sum()：求和

sd()：求总体标准差——（样本-期望）/（样本数）

var()：求样本标准差——（样本-期望）/（样本数-1）

range()：求样本数据的范围

(2) 数据展示：

summary()：展现一组数据的综合信息，返回一个list

> summary(mtcars$wt)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.513   2.581   3.325   3.217   3.610   5.424 

quantile()：根据遗嘱数据来分配概率，最小数概率对应0，最大数概率对应1

> quantile(mtcars$wt)
     0%     25%     50%     75%    100% 
1.51300 2.58125 3.32500 3.61000 5.42400 

table()：返回一组数据中，每个特异值出现的次数

> table(mtcars$cyl)

 4  6  8 
11  7 14 

2. 数据的分组

等距和等大小分组：

mtcars1 <- mtcars %>%  mutate(equal_size = ntile( qsec , 5),
                              equal_distance = cut( wt,
breaks = seq( from = min(wt), to = max(wt),  ##设置断开的位置
by = (max(wt) - min(wt)) / 5 ),  ##通过计算步长，层层递进得到最终的序列
include.lowest = T ))

ntile函数通过将数据进行排序，更具分组需要，将数据分为n个组别，返回这组数据对应位置上的数据的组别；等距分组则完全依赖于将数字区间进行军方，利用cut函数将落到不同区间里的数据进行划分，二者的划分结果实质相同；

3. 分析数据的异常值

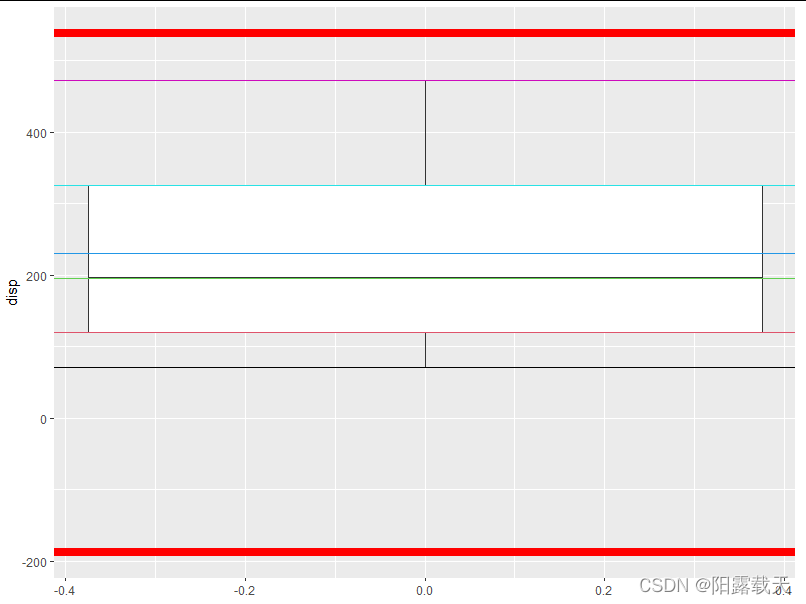
对于已知总体分布的数据常用 mean ± n*sd （n = 2,3...） 来限定样本中合理值范围，超过这些范围的可认作为异常值；对于未知参数的样本数据，有许多排除一场值的方法，一个经典的方法就是上、下四分位分别加减1.5倍的四分位范围从而限定数的上下限，在此之外的均为一异常值：

（当然在ggplot的geom_box当中，这个范围已经被默认，图中被单独列出的黑点即为异常值，此时不会有正常箱图里表示数据上下界的横线）

##先查看disp的四分位

> s <- summary( mtcars$disp)
> s
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   71.1   120.8   196.3   230.7   326.0   472.0 


##得到iqr（四分位的范围）的值

> iqr <- IQR(mtcars$disp)
> iqr
[1] 205.175


##绘图
ggplot(mtcars,aes(y = disp)) +
  geom_boxplot() +
  geom_hline(yintercept = s, color = 1:6) + ##根据summary里面的几个值，在箱图上标出对应的线
  geom_hline(yintercept = c(s[2]-1.5*iqr , s[4]+1.5*iqr), color = 'red',size = 3) ##标出上下限就
  
  

 可见数据中无异常值。

二. 数据分布

R语言内部可以依据不同分布生成随机数据，同时也可以对一列数据按照预设的分布推算其出现概率等。

1. 生成随机数

(1) rnorm()

依据随机分布生成一系列随机数：

rnorm(55, mean = 0, sd = 1)
##生成55个平均值为0，标准差为1的随机数

(2) runif / sample

生成服从于均匀分布的随机数：

> runif(17,max = 1 ,min = 0.5)
 [1] 0.7074430 0.9890402 0.9877037 0.7021419 0.5685381 0.6919902 0.7986621
 [8] 0.9996719 0.9699007 0.5763348 0.6055292 0.9353894 0.8633643 0.5103040
[15] 0.8058729 0.8509983 0.6263499

##生成17个最大值为1，最小值为0.5，默认是0~1


> sample(0:10, 15, replace = TRUE)
 [1] 4 7 8 2 0 2 6 9 1 2 7 9 0 4 6

##replace代表是否允许放回采样

(3) rbinom

根据事件发生的概率，对一定次数次实验结果进行估计，生成事件发生的次数的序列：

rbi <- rbinom(23, size = 100, prob = 0.5)
 [1] 45 60 49 44 51 45 56 39 42 50 54 54 43 58 34 52 50 51 48 39 58 48 52

##产生23个数据，其中进行100次实验，事件发生概率为0.5，生成的数字是这100次事件中事件发生的概率

(4) rpois

根据指定的lamda来生成数据：

> pos <- rpois(33 , 4)
> pos
 [1]  5  5  4  2  8  7  6 10  2  2  3  4  8  6  8  5  5  8  4  5  3  4  4
[24]  8  5  4  6  4  6  5  4  4  1

(5) rexp

指定指数，产生数列：

> rexp(11,0.5)
 [1]  0.2354817  4.2218206  1.2789491  0.5667985  6.8250768 11.7577884
 [7]  3.4183153  0.2926459  0.6410425  3.0253369  0.7224791

(6) rgamma

指定shape参数，产生数列：

> rgamma(9 , shape = 4)
[1] 4.818401 3.816967 3.380444 2.770275 4.406524 3.578493 2.511661
[8] 4.838542 3.382133

##scale默认为1

当参数 shape = 1时，伽马分布就是参数为scale的指数分布

当shape = n/2，scale = 1/2 时，伽马分布就是自由度为n的卡方分布

2. 数据的分布的分析

以上函数均由 r_<...>组成，将“r”替换分别为p、q和d，构成依照某种分布来分析数据的概率特征的函数

以正态分布为例，生成函数rnorm()

# q: 一系列下分位点（可以理解是概率一个密度函数曲线对应的x轴上的点）。函数计算计算P[x < q]
pnorm(q, mean = 0, sd = 1)


# p：系列概率（所以要求p在 0~1 内）。函数通过概率反推计算“x轴上坐标点的位置”
qnorm(p, mean = 0, sd = 1)


# x：通过x轴上坐标点计算该处的概率密度
dnorm(x, mean = 0, sd = 1)

三. 数据的统计检验

1. 数据的关联性分析

可以使用cor.test函数对两组数据的关联性进行分析：

> r <- with( mtcars, cor.test( mpg, wt ))
> r

	Pearson's product-moment correlation

data:  mpg and wt
t = -9.559, df = 30, p-value = 1.294e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.9338264 -0.7440872
sample estimates:
       cor 
-0.8676594 

## true correlation is not equal to 0 表明二者有一定相关性
## cor是关联性系数，在例子中，表面wt和mpg二者有呈现负相关的趋势
## 使用 r$ 来查看r中不同数据，说明函数返回的还是一个列表

2. 参数和非参数检验

参数检验和非参数检验的差别就在于是否关注于总体的分布情况

(1) student 检验:

使用t.test对数据进行检验,其中输入的数据的形式可分为3种，分别对应不同的检验目标

t.test(数据向量， mu = number) ：分析number是否区别于这组数据，即number这个数值在数据中是否协调；

t.test(数据向量1，数据向量2)：分析两个数据的分布差异是否显著。注意可以使用 paired = T（默认为F）参数，表明对两个数向量中的数据要一一对应着进行分析；

> t.test(mtcars$mpg,mtcars$wt,paried = T)

	Welch Two Sample t-test

data:  mtcars$mpg and mtcars$wt
t = 15.633, df = 32.633, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 14.67644 19.07031
sample estimates:
mean of x mean of y 
 20.09062   3.21725 

t.test(类别1 ~ 类别2)：类别可以是一个df中的某两列，其中一组数据levels只能由两种，分析关联性，例如分析性别（levels = 男或女）与寿命的关系

> with(mtcars,t.test(mpg,vs))  ##单纯两组数据之间的比较

	Welch Two Sample t-test

data:  mpg and vs
t = 18.382, df = 31.434, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 17.47381 21.83244
sample estimates:
mean of x mean of y 
 20.09062   0.43750 

> with(mtcars,t.test(mpg~vs))  ##关联性的分析，vs的level只有“0” “1”

	Welch Two Sample t-test

data:  mpg by vs
t = -4.6671, df = 22.716, p-value = 0.0001098
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -11.462508  -4.418445
sample estimates:
mean in group 0 mean in group 1 
       16.61667        24.55714

(2) wilcox.test()

释义：符号秩检验（Wilcoxon）；基于符号检验其秩分分布的办法，本质上是一种检验平均秩的检验。即把样本的两次观测值相减，记录差值的符号和绝对值，并基于绝对值升序求秩分，比较两组数据的正值秩分或负值秩分，从而确定其差异性。

非参数检验的一种，用法和t.test()基本语法一样，两种检验所得p值可以不同。

四. 线性回归及预测

1. lm()

用于线性拟合：

lm(formula, data, subset, weights, na.action,
   method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
   singular.ok = TRUE, contrasts = NULL, offset, ...)

对于一般的使用而言，输入合适的data和formula即可使用该函数。data为一个df，限定了formula中各个量在df中的对应关系（变量之间的关系不是随意的，而是由df中实实在在的一行中的各列间的关系相互对应起来的），formula输入待拟合的变量之间关系：

> lm.model <- lm(wt ~ mpg + hp, data = mtcars)
> lm.model

Call:
lm(formula = wt ~ mpg + hp, data = mtcars)

Coefficients:
(Intercept)          mpg           hp  
  6.2182863   -0.1455218   -0.0005277  


## 注意这里相当于构建了一个 wt = a*mpg + b*hp 的一个函数，a和b均为系数

2. 线性模型的预测

利用lm生成的模型对数据进行预测，可以提取模型的参数后，生成线性模型随后对其进行预测，当让也可以使用predict() 函数：

para <- coef(lm.model)  ##利用coef()函数提取模型里面的参数，返回一个向量方便使用；

lm.model <- lm(wt ~ mpg + hp, data = mtcars) ##加载模型
newdata <- mtcars %>% dplyr::select(hp, mpg ) ##提取原有的数据
wt.predicted <- predict( lm.modelplot, newdata )  ##利用原来的数据，结合模型，对wt进行预估
plot <-
  ggplot( data.frame( reference = mtcars$wt,  manual = wt.predicted ), ##将原wt和预测的wt分别作为两轴
          aes( reference, manual ) ) +
  geom_point() +
  geom_smooth( method = "lm", se = F ); ##geom_smooth自适应地对x轴和y轴上的元素，以lm规则进行拟合

 可见，预测数据与原有数据仍有差距，geom_smooth拟合的曲线并非 y = x  而有所偏差。