pytorch学习笔记一：张量的操作与线性回归

一、张量的简介

1、张量的基本概念

张量是一个【多维数组】，它是一个标量、向量、矩阵的高维拓展。

2、张量的属性

在 PyTorch 0.4.0 之前，torch.autograd 包中存在 Variable 这种数据类型，主要是用于封装 Tensor，进行自动求导。Variable 主要包含下面几种属性。

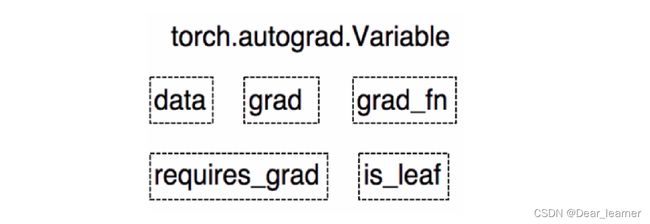
● data: 被包装的 Tensor。
● grad: data 的梯度。
● grad_fn: 创建 Tensor 所使用的 Function，是自动求导的关键，因为根据所记录的函数才能计算出导数。
● requires_grad: 指示是否需要梯度，并不是所有的张量都需要计算梯度。
● is_leaf: 指示是否叶子节点(张量)。

在 PyTorch 0.4.0 之后，Variable 并入了 Tensor。在之后版本的 Tensor 中，除了具有上面 Variable 的 5 个属性，还有另外 3 个属性。

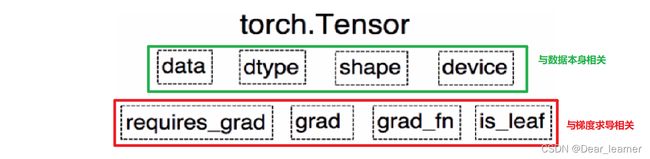
• dtype：张量的数据类型
  
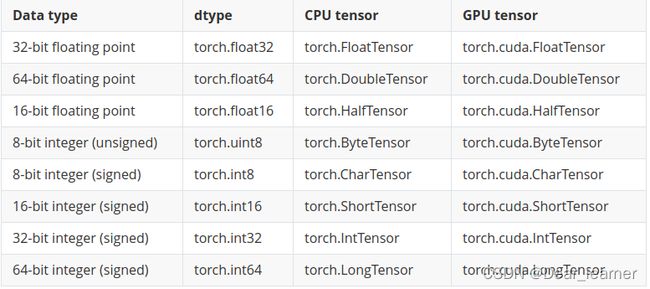
  每种类型都有CPU和GPU两个版本，张量运算必须发生在相同类型的数据之间。
• shape：张量的形状，如（1， 3， 64， 64）
• device：张量所在的设备，CPU/GPU，决定张量的计算在哪里进行，张量放在GPU上才能使用加速。

二、张量的创建

1、直接创建

torch.tensor():从data创建Tensor

torch.tensor(data, 
             dtype=None, 
             device=None, 
             requires_grad=False, 
             pin_memory=False) -> Tensor

• data：数据，可以是list，也可以是numpy
• dtype：数据类型，默认和data一致
• device：tensor所在的设备
• requires_grad：是否需要梯度，默认False，在搭建神经网络时需要将求导的参数设为True
• pin_memory：是否存于锁页内存，默认False

示例：

arr = np.ones((3, 3))
print('ndarray的数据类型：',arr.dtype)

tensor_arr = torch.tensor(arr)
print(tensor_arr)

#result
ndarray的数据类型： float64
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)

.from_numpy() 将ndarray转换成tensor，两者共享内存，当修改一个数据时另一个也会被修改

array_b = np.array([1, 2, 3, 4])
tensor_b = torch.from_numpy(array_b)
print(array_b)
print(tensor_b)
#result
[1 2 3 4]
tensor([1, 2, 3, 4], dtype=torch.int32)

array_b[0] = 5
print(array_b)
print(tensor_b)
#result
[5 2 3 4]
tensor([5, 2, 3, 4], dtype=torch.int32)

tensor_b[0] = 10
print(array_b)
print(tensor_b)
#result
[10  2  3  4]
tensor([10,  2,  3,  4], dtype=torch.int32)

2、依数值创建

torch.zeros()依size创建全0的张量，torch.ones()依据size创建值全为1的张量

torch.zeros(*size, 
            out=None, 
            dtype=None, 
            layout=torch.strided, 
            device=None, 
            requires_grad=False) -> Tensor

• size：张量的形状，如（3，3）
• layout ：这个是内存中的布局形式,有strided和sparse_coo等
• out：表示输出张量，就是再把这个张量赋值给别的一个张量，但是这两个张量时一样的，指的同一个内存地址
• device：所在的设备，gpu/cpu
• requires_grad：是否需要梯度
  示例：

out_t = torch.tensor([2])
t = torch.zeros((3, 3), out=out_t)
print(out_t)
print(t)
print(id(t), id(out_t), id(out_t)==id(t))
# result
tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
140531404201664 140531404201664 True

torch.eye()创建对角线为1的张量

torch.eye(n, m=None, 
    out=None, 
    dtype=None, 
    layout=torch.strided, 
    device=None, 
    requires_grad=False) -> Tensor

torch.zeros_like()创建与input同shape的值全为0张量，torch.ones_like()创建与input同shape的值全为1的张量

#创建与input同shape的全1张量
torch.ones_like(input, 
          dtype=None, 
          layout=None, 
          device=None, 
          requires_grad=False, 
          memory_format=torch.preserve_format) -> Tensor

out_t = torch.tensor([1, 2, 3])
print('out_t:', out_t)

t = torch.ones((3,1), out=out_t)
print('\n')
print('t:',t)
print('out_t:', out_t)
print('id(t:):', id(t), 'id(out_t):', id(out_t), id(t)==id(out_t))

inputs = torch.tensor([[1, 2], [3, 4]])
out_ = torch.ones_like(inputs)
print('\n')
print('out_:', out_)

###result
out_t: tensor([1, 2, 3])


t: tensor([[1],
        [1],
        [1]])
out_t: tensor([[1],
        [1],
        [1]])
id(t:): 2564793927864 id(out_t): 2564793927864 True


out_: tensor([[1, 1],
        [1, 1]])

torch.full()自定义数值张量

torch.full(size, 
           fill_value,
           out=None, 
           dtype=None, 
           layout=torch.strided, 
           device=None, 
           requires_grad=False) -> Tensor
# fill_value:自定义的数值

torch.full_like(input, 
                fill_value, 
                dtype=None, 
                layout=torch.strided, 
                device=None, 
                requires_grad=False, 
                memory_format=torch.preserve_format) -> Tensor

full_t = torch.full((2,3), 3)
print('full_t:', full_t)

full_like_t = torch.full_like(full_t, 5)
print('full_like_t:', full_like_t)

##result
full_t: tensor([[3, 3, 3],
        [3, 3, 3]])
full_like_t: tensor([[5, 5, 5],
        [5, 5, 5]])

torch.arange()创建等差的一维张量，数值区间[start, end)

torch.arange(start=0, 
             end, 
             step=1,   #数列公差，默认为1
             out=None, 
             dtype=None, 
             layout=torch.strided, 
             device=None, 
             requires_grad=False) -> Tensor

torch.linspace()创建均分的一维张量，包含在区间start和end均匀间隔的step个值，数值区间[start, end]

torch.linspace(start, 
         end, steps, # steps指数列的长度
         out=None,
         dtype=None,
         layout=torch.strided,
         device=None, 
         requires_grad=False) -> Tensor

torch.arange(1, 10, 2)
#result
tensor([1, 3, 5, 7, 9])

torch.linspace(1, 10, 5)
#result
tensor([ 1.0000,  3.2500,  5.5000,  7.7500, 10.0000])
#这里step的计算是(end-start)/(step-1)

torch.logspace()创建对数均分的一维张量，数值区间为[start, end]，长度为steps，底为base默认为10

logspace(start, end, steps, 
         base=10.0,
         out=None, 
         dtype=None, 
         layout=torch.strided, 
         device=None, 
         requires_grad=False) -> Tensor

torch.logspace(2, 10, 6)
#result
tensor([1.0000e+02, 3.9811e+03, 1.5849e+05, 6.3096e+06, 2.5119e+08, 1.0000e+10])

3、依概率创建

torch.normal()生成正态分布，torch.randn()生成标准正态分布，torch.randn_like()生成标准正态分布，shape同input相同，torch.rand()、torch.rand_like()生成区间[0,1)上的均匀分布，torch.randint()、torch.randint_like()生成区间[low, high)区间上的均匀分布

#mean和std都是标量，需要设置size
torch.normal(0, 4, (4,5))
#result
tensor([[-0.3452, -0.9280, -1.2737,  2.4642, -2.8298],
        [ 2.2866, -2.7351,  2.5361, -3.3591,  0.3584],
        [-2.0955,  8.1288, -4.2677,  4.1769, -7.6397],
        [ 0.4677, -1.8013, -5.2755, -4.9442, -1.4894]])

#mean为张量，std标量
mean = torch.arange(1, 5, dtype=torch.float)
std = 1
torch.normal(mean, std)
#result
tensor([0.6424, 1.6814, 2.6214, 3.7179])

#mean为标量，std为张量
mean = 2
std = torch.ones((2, 3))
torch.normal(mean, std)
#result
tensor([[2.3587, 3.1138, 2.5852],
        [3.0468, 1.3177, 3.0816]])

#mean为张量，std为张量
mean = torch.arange(1, 5, dtype=torch.float)
std = torch.arange(1, 5, dtype=torch.float)
torch.normal(mean, std)
#result
tensor([ 3.9392,  2.5605,  5.2616, -2.8300])

#生成标准正态分布
torch.rand((3,4))
#result
tensor([[0.4366, 0.1921, 0.0110, 0.4311],
        [0.9431, 0.5463, 0.1594, 0.0875],
        [0.1984, 0.9109, 0.9961, 0.0784]])

ones = torch.ones((4, 4))
torch.rand_like(ones)
#result
tensor([[0.9565, 0.2871, 0.9714, 0.4637],
        [0.9190, 0.6885, 0.1923, 0.9143],
        [0.2151, 0.0512, 0.9051, 0.4186],
        [0.5376, 0.9068, 0.0917, 0.1121]])

torch.randperm()生成0-n-1的随机排列，常用于生成索引；torch.bernoulli()以input为概率生成伯努利分布

torch.randperm(5)
#result
tensor([0, 4, 2, 3, 1])

#生成范围为[0,1]的均匀随机矩阵
a = torch.empty(3, 3).uniform_(0, 1)
torch.bernoulli(a)
#result
tensor([[1., 1., 0.],
        [0., 1., 1.],
        [1., 1., 1.]])

b = torch.ones((3,3))
torch.bernoulli(b)
#result
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])

c = torch.zeros((3,3))
torch.bernoulli(c)
#result
tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])

三、张量的操作

1、张量的拼接

● torch.cat()将tensor序列按维度进行拼接，不会扩张张量的维度
● torch.stack()将tensor序列在新建的维度上进行拼接，会扩张张量的维度

t = torch.ones((2,3))
print('t:',t)

t_0 = torch.cat([t, t], dim=0)
print('\n')
print('t_0:',t_0)

t_1 = torch.cat([t, t], dim=1)
print('\n')
print('t_1:',t_1)

t_2 = torch.stack([t, t, t], dim=0)
print('\n')
print('t_2:', t_2)
print('t_2 shape:', t_2.shape)

t_3 = torch.stack([t, t, t], dim=1)
print('\n')
print('t_3:', t_3)
print('t_3 shape:', t_3.shape)

#####result#####
t: tensor([[1., 1., 1.],
        [1., 1., 1.]])


t_0: tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])


t_1: tensor([[1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.]])


t_2: tensor([[[1., 1., 1.],
         [1., 1., 1.]],

        [[1., 1., 1.],
         [1., 1., 1.]],

        [[1., 1., 1.],
         [1., 1., 1.]]])
t_2 shape: torch.Size([3, 2, 3])


t_3: tensor([[[1., 1., 1.],
         [1., 1., 1.],
         [1., 1., 1.]],

        [[1., 1., 1.],
         [1., 1., 1.],
         [1., 1., 1.]]])
t_3 shape: torch.Size([2, 3, 3])

2、张量的切分

.chunk()：将张量按维度进行平均切分，返回值是张量列表

torch.chunk(input, chunks, dim=0) -> List of Tensors
#input:需要切分的张量
#chunks：切分的份数
#dim：维度
#若不能平均切分，最后一个张量小于其他张量

a = torch.ones((2, 7))  
a_chunk = torch.chunk(a, dim=1, chunks=3)   

for idx, t in enumerate(a_chunk):
    print('第{}个张量:{},shape is {}'.format(idx, t, t.shape))
    
 ####result
第0个张量:tensor([[1., 1., 1.],
        [1., 1., 1.]]),shape is torch.Size([2, 3])
第1个张量:tensor([[1., 1., 1.],
        [1., 1., 1.]]),shape is torch.Size([2, 3])
第2个张量:tensor([[1.],
        [1.]]),shape is torch.Size([2, 1])

.split() 按维度dim将张量进行切分

torch.split(tensor, 
            split_size_or_sections, 
            dim=0)
# tensor:要切分的张量
# split_size_or_sections:为int时表示每一份的切分长度，为list时，按list元素进行切分
# dim:要切分的维度

t = torch.ones((2, 5))
# list里面的元素之和要和tensor的长度要一样，否则会报错。如果是[2, 1, 1]就报错
list_of_tensors = torch.split(t, [2, 1, 2], dim=1)  

for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))
    
 ###result
第1个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
第2个张量：tensor([[1.],
        [1.]]), shape is torch.Size([2, 1])
第3个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])

3、张量的索引

● 切片索引：与numpy的操作类似
● .index_select()在维度dim上按index索引数据
● .masked_select()按mask中的True进行索引数据,返回一维的张量

t = torch.arange(6).reshape(3,2)
idx = torch.tensor([1, 2])
t_idx = torch.index_select(t, dim=0, index=idx)
# index的指定类型为torch.long
print('t:', t)
print('t_idx:', t_idx)

###result
t: tensor([[0, 1],
        [2, 3],
        [4, 5]])
t_idx: tensor([[2, 3],
        [4, 5]])

t = torch.randint(0, 9, size=(3, 3))
#.ge()选择大于等于5的值
mask = t.ge(5)  
t_select = torch.masked_select(t, mask)
print("t:\n{}\nmask:\n{}\nt_select:\n{} ".format(t, mask, t_select))

###result
t:
tensor([[8, 1, 6],
        [0, 7, 3],
        [7, 1, 7]])
mask:
tensor([[ True, False,  True],
        [False,  True, False],
        [ True, False,  True]])
t_select:
tensor([8, 6, 7, 7, 7])

4、张量变换

• .reshape()变换张量的形状，当张量在内存中是连续时，新张量和input共享数据内存
• .view()只能改变连续的（contiguous）张量，返回的张量和原张量共享基础数据
• .resize_()改变数据的形状时，只截取一部分数据

x = torch.randn(3, 4)
print(x.shape)
x=x.permute(1,0)
print(x.shape)
print(x.is_contiguous())

##result
torch.Size([3, 4])
torch.Size([4, 3])
False

#非连续状态下使用.reshape()和.view()
x = x.view(3,4)

x = x.reshape(3,4)
print(x.shape)

###result
torch.Size([3, 4])

#使用.contiguous()将tensor变成连续的
x=x.contiguous()
print(x.is_contiguous())

x=x.view(1,12)
print(x.shape)
x=x.reshape(2,6)
print(x.shape)

###result
True
torch.Size([1, 12])
torch.Size([2, 6])

x = torch.tensor([[1, 2], [3, 4], [5, 6]])
x.resize_(2, 2)
print(x)

###result
tensor([[1, 2],
        [3, 4]])

• .transpose()交换张量的两个维度。常用于图像的变换，比如把chw变换为hwc
• .T对二维张量的转置
• permute:可以对多个维度进行变换
• .squeeze()压缩长度为1的维度，dim若为None，移除所有长度为1的轴，若指定维度，当且仅当该轴的长度为1时，可以被移除
• .unsqueeze():依据dim扩张维度

t = torch.rand((2, 3, 4))
t_transpose = torch.transpose(t, dim0=1, dim1=2)
print(t_transpose.shape)
###result
torch.Size([2, 4, 3])

t = torch.arange(6).reshape(2,3)
print(t.T.shape)
###result
torch.Size([3, 2])

t = torch.rand((1,3, 4, 4))
print(t.squeeze(0).shape)
print(t.unsqueeze(2).shape)
###result
torch.Size([3, 4, 4])
torch.Size([1, 3, 1, 4, 4])

• expand：broadcasting
• repeat：memory copies

a = torch.rand(4, 32, 14, 14)
b = torch.rand(1, 32, 1, 1)
b.expand(4, 32, 14, 14).shape    # torch.Size([4, 32, 14, 14])
b.expand(-1, 32, -1, -1).shape   # torch.Size([1, 32, 1, 1])
#维度不变则可以用-1，其他负数没有意义
b.expand(-1, 32, -1, -4).shape   # torch.Size([1, 32, 1, -4])

#reshape是将维度复制多少次
b.repeat(4, 32, 1, 1).shape      # torch.Size([4, 1024, 1, 1])
b.repeat(4, 1, 32, 32).shape     # torch.Size([4, 32, 32, 32])

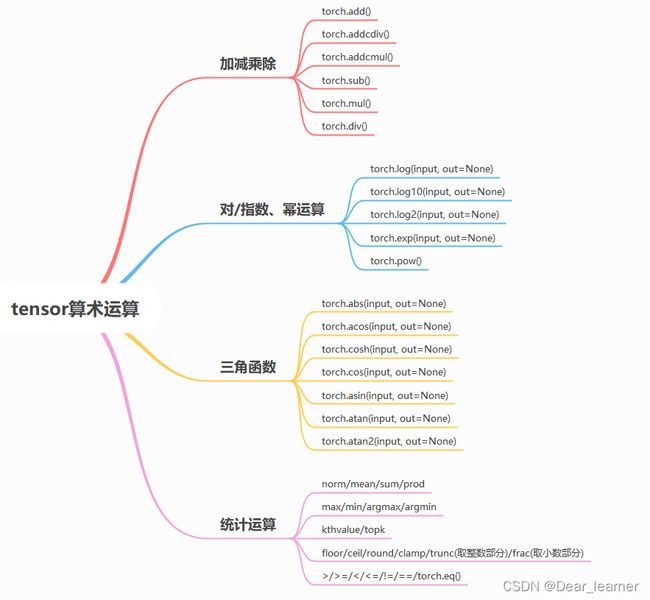
5、算术运算

6、高级操作

• torch.where():按照一定的规则合并两个tensor
• torch.where(condition, a, b)其中参数condition为条件限制，若满足condition，则为a，否则为b

a = torch.tensor([[0.0349,  0.0670, -0.0612, 0.0280, -0.0222,  0.0422],
         [-1.6719,  0.1242, -0.6488, 0.3313, -1.3965, -0.0682],
         [-1.3419,  0.4485, -0.6589, 0.1420, -0.3260, -0.4795]])
b = torch.tensor([[-0.0658, -0.1490, -0.1684, 0.7188,  0.3129, -0.1116],
         [-0.2098, -0.2980,  0.1126, 0.9666, -0.0178,  0.1222],
         [ 0.1179, -0.4622, -0.2112, 1.1151,  0.1846,  0.4283]])
cc = torch.where(a>0,a,b)     #合并a,b两个tensor，如果a中元素大于0，则c中与a对应的位置取a的值，否则取b的值
print(cc)
### result
tensor([[ 0.0349,  0.0670, -0.1684,  0.0280,  0.3129,  0.0422],
        [-0.2098,  0.1242,  0.1126,  0.3313, -0.0178,  0.1222],
        [ 0.1179,  0.4485, -0.2112,  0.1420,  0.1846,  0.4283]])

• torch.gather():收集输入维度上指定位置的参数

参数：
input(tensor)：输入tensor
dim(int):带操作的维度
index(LongTensor):如何对input进行操作
output(tensor)：输出和index的维度是一致的

input = [
    [2, 3, 4, 5, 0, 0],
    [1, 4, 3, 0, 0, 0],
    [4, 2, 2, 5, 7, 0],
    [1, 0, 0, 0, 0, 0]
]
input = torch.tensor(input)
#注意index的类型
length = torch.LongTensor([[4],[3],[5],[1]])
#index之所以减1,是因为序列维度是从0开始计算的
out = torch.gather(input, 1, length-1)
### result
tensor([[5],
        [3],
        [7],
        [1]])

# torch.gather()利用index来索引input指定位置上的值

四、线性回归模型

线性回归是分析一个变量与另外一(多)个变量之间关系的方法。因变量是 y，自变量是 x，关系线性：
y = w×x + b
任务是求解w、b

求解步骤：
1、确定模型：y = wx + b
2、选择损失函数：

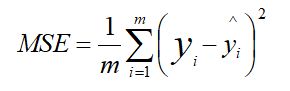
3、求解梯度并更新：
w = w - lr * w.grad
b = b - lr * b.grad
4、实现：

import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)

lr = 0.05  # 学习率

# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)
# torch.randn(20, 1) 用于添加噪声
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1)

# 构建线性回归参数
w = torch.randn((1), requires_grad=True) # 设置梯度求解为 true
b = torch.zeros((1), requires_grad=True) # 设置梯度求解为 true

# 迭代训练 1000 次
for iteration in range(1000):

    # 前向传播，计算预测值
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)

    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 反向传播
    loss.backward()

    # 更新参数
    b.data.sub_(lr * b.grad)
    w.data.sub_(lr * w.grad)

    # 每次更新参数之后，都要清零张量的梯度
    w.grad.zero_()
    b.grad.zero_()

    # 绘图，每隔 20 次重新绘制直线
    if iteration % 20 == 0:

        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
        plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
        plt.pause(0.5)
        plt.show()

        # 如果 MSE 小于 1，则停止训练
        if loss.data.numpy() < 1:
            break