【Paper Notes】TensoRF: Tensorial Radiance Fields
论文链接
TensoRF: Tensorial Radiance Fields 是上海科技大学和Adobe合作发表的一篇文章。最终发表于ECCV 2022上。
论文目标
三维场景的表示方法有很多,比如Mesh,Voxel Grid,或者基于神经网络的表示方法 NeRF1 。本文提出了一种很新颖的表示三维场景的方法,主要是利用4D tensor的分解基础,将三维场景分解为多个向量的外积和,或者多个向量和矩阵的外积和。这种方式的好处是比基于NeRF 1 的方法使用的显存更小,并且表示场景的方式更加紧凑。
数学原理
在深入论文前,首先我们学习一下基本的数学原理。
SVD分解回顾
我们首先可以回顾一下SVD分解的形式。
给定一个矩阵 A m × n A_{m\times n} Am×n, 我们可以将该矩阵分解为
A m × n = U m × m Σ m × n V n × n H A_{m\times n} = U_{m\times m} \Sigma_{m\times n} V_{n \times n}^H Am×n=Um×mΣm×nVn×nH
我们知道
Σ m × n = [ Σ 1 0 0 0 ] \Sigma_{m\times n} = \begin{bmatrix} \Sigma_1 & \bold{0} \\ \bold{0} & \bold{0} \end{bmatrix} Σm×n=[Σ1000]
其中 Σ 1 = d i a g ( σ 1 , σ 2 , ⋯ , σ r ) \Sigma_1 = {\rm diag} ( \sigma_1, \sigma_2, \cdots , \sigma_r ) Σ1=diag(σ1,σ2,⋯,σr) 。同时,我们也知道 U m × m = [ u 1 ⋯ u r , 0 ⋯ 0 ] U_{m\times m} =[\bold{u}_1 \cdots \bold{u}_r, \bold{0} \cdots \bold{0}] Um×m=[u1⋯ur,0⋯0], V n × n = [ v 1 ⋯ v r , 0 ⋯ 0 ] V_{n\times n}=[\bold{v}_1 \cdots \bold{v}_r, \bold{0} \cdots \bold{0}] Vn×n=[v1⋯vr,0⋯0]。
那么将SVD分解写成向量表达的形式就是
A = ∑ i = 1 r σ i u i v i H = ∑ i = 1 r σ i ( u i × v ^ i ) A = \sum_{i=1}^r \sigma_i \bold{u}_i \bold{v}_i^H = \sum_{i=1}^r \sigma_i (\bold{u}_i \times \bold{\hat v}_i) A=i=1∑rσiuiviH=i=1∑rσi(ui×v^i)
其中, × \times × 表示外积,^ 表示逐元素共轭。通过SVD分解,我们可以将一个二维矩阵表达成多个一维向量外积加和的方式。
CP 分解
如果我们面邻的矩阵不再是2D的,而是3D的矩阵,那么如何做分解呢?其实可以套用SVD的形式,先把3D的矩阵,某两个维度压扁成2D的矩阵,然后逐步进行SVD分解。CP分解的目标是将高维矩阵分解成多个向量内积加权的方式。下面以3D 张量为例子分析。
假定 T ∈ R I × J × K \mathcal{T}\in \mathbb{R}^{I \times{J}\times {K}} T∈RI×J×K, 那么 T \mathcal{T} T 可以分解为
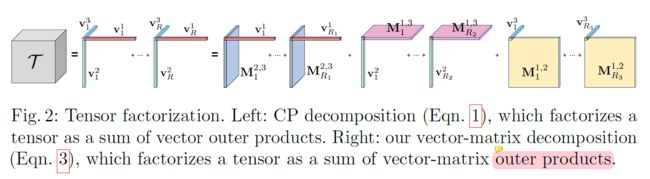
T = ∑ r = 1 R v r 1 × v r 2 × v r 3 \mathcal{T}=\sum\limits_{r=1}^R\bold{v}_r^1\times \bold{v}_r^2 \times\bold{v}_r^3 T=r=1∑Rvr1×vr2×vr3
其中 v 1 ∈ R I , v 2 ∈ R J , v 3 ∈ R K \bold{v}^1 \in \mathbb{R}^I,\bold{v}^2 \in \mathbb{R}^J,\bold{v}^3 \in \mathbb{R}^K v1∈RI,v2∈RJ,v3∈RK 分别对应矩阵的第一个维度,第二个维度和第三个维度。
那么如果我们想得到原始矩阵某个 i , j , k i,j,k i,j,k位置的值该如何计算呢?
T i , j , k = ∑ r = 1 R v r , i 1 v r , j 2 v r , k 3 \mathcal{T}_{i,j,k} = \sum\limits_{r=1}^R \bold{v}_{r,i}^1\bold{v}_{r,j}^2\bold{v}_{r,k}^3 Ti,j,k=r=1∑Rvr,i1vr,j2vr,k3
VM 分解 (论文提出的方法,Vector-Matrix Decomposition)
虽然CP的表示方法非常紧凑,但是依赖几个秩为1的张量加和表示三维场景,可能需要分解出非常多的加和项。因此论文中又提出了一种松弛的方法,期望减少 R R R项的个数。具体的做法是这样的
T = ∑ r = 1 R v r 1 × M r 2 , 3 + ∑ r = 1 R v r 2 × M r 1 , 3 + ∑ r = 1 R v r 3 × M r 1 , 2 \mathcal{T} = \sum\limits_{r=1}^R \bold{v}_r^1 \times \bold{M}_r^{2,3} + \sum\limits_{r=1}^R \bold{v}_r^2 \times \bold{M}_r^{1,3} + \sum\limits_{r=1}^R \bold{v}_r^3 \times \bold{M}_r^{1,2} T=r=1∑Rvr1×Mr2,3+r=1∑Rvr2×Mr1,3+r=1∑Rvr3×Mr1,2
这样,我们就将外积分解成了一个向量对一个二维矩阵的内积,直观的说可以理解成,一个轴(x/y/z)对一个平面(y-z/x-z/x-y)平面的外积。其中 M r 1 , 2 ∈ R I × J , M r 1 , 3 ∈ R I × K , M r 2 , 3 ∈ R J × K \bold{M}_{r}^{1,2}\in\mathbb{R}^{I\times J},\bold{M}_{r}^{1,3}\in\mathbb{R}^{I\times K},\bold{M}_{r}^{2,3}\in\mathbb{R}^{J\times K} Mr1,2∈RI×J,Mr1,3∈RI×K,Mr2,3∈RJ×K。
如图所示:
论文方法
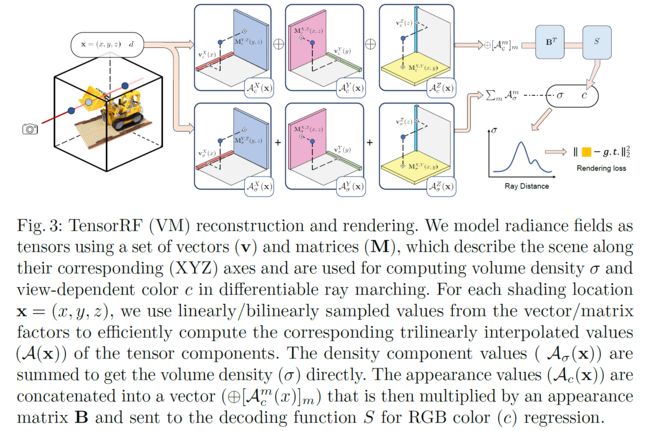
了解了以上数学原理,我们知道,我们可以通过多个向量,来重建出3D的张量。但是针对三维场景,其是一个3D的张量 x , y , z x,y,z x,y,z 表示占据密度,一个4D的张量 x , y , z , c x,y,z,c x,y,z,c 表示颜色信息。针对这种形式如何建模呢?
首先对于密度 σ \sigma σ, 我们可以直接用以上的CP或者VM进行建模,但是对于颜色信息来说,是一个4D的张量。我们可以仿照CP分解,构造出4D张量的分解方式:
T = ∑ r = 1 R v r 1 × v r 2 × v r 3 × v r 4 , T ∈ R I × J × K × P \mathcal{T}=\sum\limits_{r=1}^R\bold{v}_r^1\times \bold{v}_r^2 \times\bold{v}_r^3 \times \bold{v}_r^4, \\ \mathcal{T} \in \mathbb{R}^{I\times J \times K \times P} T=r=1∑Rvr1×vr2×vr3×vr4,T∈RI×J×K×P
其中P是计算颜色所需要的通道个数,用于恢复颜色。
如果用VM分解来构造该4D张量,同样需要添加一个秩为1的向量 b \bold{b} b, 具体可以写为
T = ∑ r = 1 R v r 1 × M r 2 , 3 × b 3 r − 2 + ∑ r = 1 R v r 2 × M r 1 , 3 × b 3 r − 1 + ∑ r = 1 R v r 3 × M r 1 , 2 × b 3 r \mathcal{T} = \sum\limits_{r=1}^R \bold{v}_r^1 \times \bold{M}_r^{2,3}\times \bold{b}_{3r-2} + \sum\limits_{r=1}^R \bold{v}_r^2 \times \bold{M}_r^{1,3}\times \bold{b}_{3r-1}+ \sum\limits_{r=1}^R \bold{v}_r^3 \times \bold{M}_r^{1,2}\times \bold{b}_{3r} T=r=1∑Rvr1×Mr2,3×b3r−2+r=1∑Rvr2×Mr1,3×b3r−1+r=1∑Rvr3×Mr1,2×b3r
其中 1,2,3上标分别对应于 x , y , z x,y,z x,y,z维度。
渲染细节
另外一个需要关注的问题是,这种方式表示的是一个网格,那么如果采样点是浮点的话,如何表示呢?文章给出了一种解决思路就是通过插值来表示,比如采样 x 1 , y 1 , z 1 x_1,y_1,z_1 x1,y1,z1, 那么我们可以通过一次或者二次插值得到 v 1 ( x 1 ) , M 1 , 3 ( x 1 , z 1 ) \bold{v}^1(x_1), \bold{M}^{1,3}(x_1,z_1) v1(x1),M1,3(x1,z1)。
还有一个问题是,最终得到的4D张量,最后一个维度是 P P P, 并不是3通道的颜色。需要通过MLP变换,或者SH函数映射到图像上。
实验结果
文章给出了一些实验结果,在渲染效果其实并没有特别惊艳,更多的是关注减少了NeRF的训练时间,并且减少了渲染场景所用的显存。