【Python】Gamma分布详解
文章目录
-
- 初步介绍
- 形状特征
初步介绍
在学习Gamma分布之前,有必要复习一下Poisson分布:泊松分布
Poisson分布指的是,单个事件在某一刻发生的概率。Gamma分布更进一步,指的是某个事件在某个时刻发生第 n n n次的概率。
p ( x ) = x k − 1 e − λ x λ k Γ ( k ) p(x)=x^{k-1}\frac{e^{-\lambda x}}{\lambda^k\Gamma(k)} p(x)=xk−1λkΓ(k)e−λx
其中, k k k为形状参数, λ \lambda λ为尺度参数,固定尺度参数 λ \lambda λ,给定不同的 k k k值,可得到不同型形状的 Γ \Gamma Γ分布的概率曲线
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import gamma
for k in [0.8, 1.5, 3.5]:
xs = gamma(k, size=20000)
plt.hist(xs, 200, range=(0,10),
alpha=0.5, label=f"k={k}")
plt.legend()
plt.show()
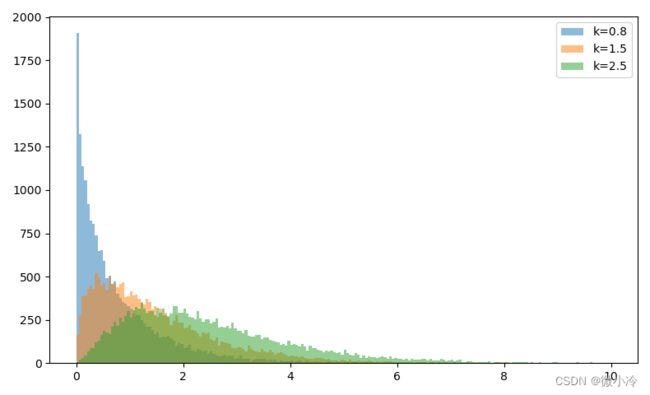
其分布如下图所示
形状特征
一般来说,当 k < 1 k<1 k<1时, p ( x ) p(x) p(x)为单调递减函数,对应图中 k = 0.8 k=0.8 k=0.8时,概率密度逐渐下降的情况;当 k ∈ ( 1 , 2 ) k\in(1,2) k∈(1,2)时, p ( x ) p(x) p(x)先上凸,然后下凸,由于上图画的是随机点的直方图,所以对凹凸性的展现并不明显。当 k > 2 k>2 k>2时, p ( x ) p(x) p(x)在增函数区间,是先下凸然后上凸的。
特别地,当 k = 1 k=1 k=1时, Γ \Gamma Γ分布的概率密度变为
p ( x ) = e − λ x λ p(x)=\frac{e^{-\lambda x}}{\lambda} p(x)=λe−λx
此为指数分布,有关指数分布,请看这里Pyhton威布尔分布
令 k = n 2 k=\frac n 2 k=2n, λ = 1 2 \lambda=\frac12 λ=21,则其表达式变为
p ( x ) = x n 2 − 1 e − λ 2 2 n 2 Γ ( n 2 ) p(x)=\frac{x^{\frac{n}{2}-1}e^{-\frac{\lambda}{2}}}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})} p(x)=22nΓ(2n)x2n−1e−2λ
此即具有 n n n个自由度的卡方分布,有关卡方分布请戳这里:Python卡方分布
尺度因子 k k k可以调整分布曲线的胖瘦,需要注意的是,在gamma函数中,输入的尺度因子是 λ \lambda λ的倒数。接下来对 λ = 2 , 1 , 0.5 \lambda=2, 1, 0.5 λ=2,1,0.5这三种情况进行仿真
ks = [0.8, 1.5, 3.5]
fig = plt.figure()
for i in range(3):
ax = fig.add_subplot(1,3,i+1)
ax.set_title(f"k={ks[i]}")
for lam in [1/2, 1, 2]:
xs = gamma(ks[i], lam, size=20000)
ax.hist(xs, 200, range=(0,10),
alpha=0.5, label=f"lambda={1/lam}")
plt.legend()
plt.show()
得到不同k值时的分布情况
可见, λ \lambda λ越小,则分布越矮胖。
最后,测试一下 Γ \Gamma Γ函数的期望与方差,根据其概率密度函数,可以求得其期望和方差分别为
E = k λ , σ 2 = k λ 2 E=\frac{k}{\lambda}, \sigma^2=\frac{k}{\lambda^2} E=λk,σ2=λ2k
接下来对其进行测试
k, lam = 1.5, 2
xs = gamma(k, 1/lam, size=20000)
print("理论期望", k/lam, "\t理论方差", k/lam**2)
print("实际期望", np.mean(xs), "\t实际方差", np.cov(xs))
得到输出
理论期望 0.75 理论方差 0.375
实际期望 0.7550140115027265 实际方差 0.3794021804397493