人工智能-机器学习-决策树与随机森林
一.数据集的纯度
决策树的关键在于当前状态下选择哪个属性作为分支条件。最佳分类属性这种“最佳性”可以用非纯度(impurity)进行衡量。如果一个数据集合中只有一种分类结果,则该集合最纯,即一致性好;如果有许多分类,则不纯,即一致性不好。
有很多指标定义不纯度,根据不同判定不纯度的目标函数:
1.ID3 算法
ID3算法的核心是“信息熵”:
1. 熵作为衡量样本纯度的标准,熵越大,越不纯。
2. 希望在分类以后能够降低熵的大小,变纯一些。
3. 分类后熵变小可以用信息增益(Information Gain)来衡量。
4. 每次划分选取信息增益最高的属性为划分标准,重复这个过程,直至生成一个能完美分类训练样例的决策树。
1.1 计算数据集 D 的经验熵H(D)
H ( D ) = − ∑ k = 1 k ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ H(D) = -\sum_{k=1}^k \frac{\lvert C_k \lvert}{\lvert D \lvert} \log_2 \frac{\lvert C_k \lvert}{\lvert D\lvert} H(D)=−k=1∑k∣D∣∣Ck∣log2∣D∣∣Ck∣
1.2 计算特征A对数据集D的经验条件熵H(D|A)
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 k ∣ D i k ∣ ∣ D i ∣ log 2 ∣ D i k ∣ ∣ D i ∣ H(D|A) = \sum_{i=1}^n \frac{\lvert D_i \lvert}{\lvert D \lvert}H(D_i) = -\sum_{i=1}^n \frac{\lvert D_i \lvert}{\lvert D \lvert} \sum_{k=1}^k \frac{\lvert D_{ik} \lvert}{\lvert D_i \lvert} \log_2 \frac{\lvert D_{ik} \lvert}{\lvert D_i\lvert} H(D∣A)=i=1∑n∣D∣∣Di∣H(Di)=−i=1∑n∣D∣∣Di∣k=1∑k∣Di∣∣Dik∣log2∣Di∣∣Dik∣
1.3 计算信息增益
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A) = H(D) - H(D|A) g(D,A)=H(D)−H(D∣A)
例: 当前有10个礼物, 6个是喜欢的, 4个是不喜欢的, 礼物的特征为 [颜色, 价格, 大小]
a. 颜色的信息增益
黑色的礼物有6个, 5个是喜欢的, 1个是不喜欢的
白色的礼物有4个, 1个是喜欢的, 3个是不喜欢的
"""
信息增益: ID3(求颜色的信息增益)
"""
import math
# 计算颜色的信息增益
# 一. 未划分前的信息熵
root_entropy = - (6 / 10) * math.log(6 / 10, 2) - (4 / 10) * math.log(4 / 10, 2)
# 二. 颜色划分后的数据集的信息熵
black_node_entropy = - (5 / 6) * math.log(5 / 6, 2) - (1 / 6) * math.log(1 / 6, 2)
white_node_entropy = - (1 / 4) * math.log(1 / 4, 2) - (3 / 4) * math.log(3 / 4, 2)
sub_nodes_entropy = 6 / 10 * black_node_entropy + 4 / 10 * white_node_entropy
# 三. 信息增益
info_gain = root_entropy - sub_nodes_entropy
print(info_gain)
0.256425891682003
b. 价格的信息增益
价高的礼物有5个, 3个是喜欢的, 2个是不喜欢的
价低的礼物有5个, 3个是喜欢的, 2个是不喜欢的
"""
信息增益: ID3(求价格的信息增益)
"""
import math
# 计算价格的信息增益
# 一. 未划分前的信息熵
root_entropy = - (6 / 10) * math.log(6 / 10, 2) - (4 / 10) * math.log(4 / 10, 2)
# 二. 价格划分后的数据集的信息熵
high_node_entropy = - (3 / 5) * math.log(3 / 5, 2) - (2 / 5) * math.log(2 / 5, 2)
low_node_entropy = - (3 / 5) * math.log(3 / 5, 2) - (2 / 5) * math.log(2 / 5, 2)
sub_nodes_entropy = 5 / 10 * high_node_entropy + 5 / 10 * low_node_entropy
# 三. 信息增益
info_gain = root_entropy - sub_nodes_entropy
print(info_gain)
0.0
c. 大小的信息增益
价高的礼物有5个, 3个是喜欢的, 2个是不喜欢的
价低的礼物有5个, 3个是喜欢的, 2个是不喜欢的
"""
信息增益: ID3(求大小的信息增益)
"""
import math
# 计算大小的信息增益
# 一. 未划分前的信息熵
root_entropy = - (6 / 10) * math.log(6 / 10, 2) - (4 / 10) * math.log(4 / 10, 2)
# 二. 大小划分后的数据集的信息熵
big_node_entropy = - (4 / 6) * math.log(4 / 6, 2) - (2 / 6) * math.log(2 / 6, 2)
small_node_entropy = - (2 / 4) * math.log(2 / 4, 2) - (2 / 4) * math.log(2 / 4, 2)
sub_nodes_entropy = 6 / 10 * big_node_entropy + 4 / 10 * small_node_entropy
# 三. 信息增益
info_gain = root_entropy - sub_nodes_entropy
print(info_gain)
0.01997309402197489
可以看到, 按照价格划分的信息增益最高, 其次为大小, 最后为价格。
ID3算法的一些性质:
1.如果特征中有K个不同的取值情况, 那么ID3中可以是K叉树分支。
2.如果用完一个特质, 那么在子分支上就可以不用计算了。
3.如果是连续型特征, 则我们需要将之转换为离散型特征: a. 分桶离散, 转为离散型特征 b. 用分桶离散的边界值作为分割点切分
4. 树不一定是对称的。
2.C4.5 算法
C4.5 为一种分类算法, ID3的信息增益有一个缺点, 它一般会优先选择有较多属性值的特征, 解决方法是增加惩罚项, C4.5使用信息增益比率(gain ratio)。
S p l i t I n f o r m a t i o n ( D , A ) = − ∑ i = 1 N ∣ D i ∣ ∣ D ∣ log ∣ D i ∣ ∣ D ∣ SplitInformation(D,A) = -\sum_{i=1}^N \frac{\lvert D_i \lvert}{\lvert D \lvert} \log \frac{\lvert D_i \lvert}{\lvert D\lvert} SplitInformation(D,A)=−i=1∑N∣D∣∣Di∣log∣D∣∣Di∣
G a i n R a t i o ( D , A ) = g ( D , A ) S p l i t I n f o r m a t i o n ( D , A ) GainRatio(D,A) = \frac{g(D,A)}{SplitInformation(D,A)} GainRatio(D,A)=SplitInformation(D,A)g(D,A)
3.CART 算法
CART 算法(Classification and Regression Tree)可以进行分类和回归,
3.1 分类树使用最小GINI指数来选择划分
G i n i ( D ) = 1 − ∑ i = 0 N ( D i D ) 2 Gini(D) =1 -\sum_{i=0}^N( \frac{D_i}{D})^2 Gini(D)=1−i=0∑N(DDi)2
G i n i ( D ∣ A ) = ∑ j = 0 k D j D G i n i ( D j ) Gini(D|A) =\sum_{j=0}^k\frac{D_j}{D}Gini(D_j) Gini(D∣A)=j=0∑kDDjGini(Dj)
基尼系数越小, 代表数据越纯
3.2 回归树使用 MSE作为损失函数
m i n [ 1 n R 1 ∑ x i ∈ R 1 ( y i − c 1 ) 2 + 1 n R 2 ∑ x i ∈ R 2 ( y i − c 2 ) 2 ] min \left[ \frac{1}{n_{R_1}} \sum_{x_i \in R_1}(y_i -c_1)^2 + \frac{1}{n_{R_2}} \sum_{x_i \in R_2}(y_i -c_2)^2\right] min[nR11xi∈R1∑(yi−c1)2+nR21xi∈R2∑(yi−c2)2]
二.决策树
1.sklearn提供的决策树
可以使用 sklearn下tree 包的 DecisionTreeClassifier 进行决策树分析, 并使用 pydot 打印树结构图
安装 pydot 所需文件链接:
1. 安装 graphviz-2.38.msi
2. 安装 graphviz-0.8.1-py2.py3-none-any.whl
3. 安装 pydot-1.2.3-py2.py3-none-any.whl
4. 如果报错 则将 graphviz-2.38.msi 安装的地方的bin目录加到环境变量里
5. 如果报: module ‘os‘ has no attribute ‘errno‘
6. 找到python安装环境下的 Lib\site-packages, 如: D:\Procedure\python37\Lib\site-packages, 修改: pydot.py 1880行, 去掉 os, 直接引入 import errno
"""
决策树划分礼物是否喜欢
"""
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import LabelEncoder
import numpy as np
from sklearn import tree
import pydot
# 决策树分类
# 构建喜欢礼物数据集
# (1) 前处理
# [1,0,1] 代表 一个样本的颜色,价格,大小特征
# 一. 准备数据
train_x = np.array([["黑色", "贵重", "大"], ["白色", "贵重", "大"], ["黑色", "便宜", "大"], ["黑色", "贵重", "小"]])
train_y = np.array([["喜欢"], ["不喜欢"], ["不喜欢"], ["喜欢"]])
# 将文本数据进行 label encoder 硬编码
train_x[:, 0] = LabelEncoder().fit_transform(train_x[:, 0])
train_x[:, 1] = LabelEncoder().fit_transform(train_x[:, 1])
train_x[:, 2] = LabelEncoder().fit_transform(train_x[:, 2])
train_y[:, 0] = LabelEncoder().fit_transform(train_y[:, 0])
print(train_x)
print(train_y)
# 二. 构建树的分类器
# 构建决策树模型, 树深度设为 10
model = DecisionTreeClassifier(max_depth=10)
# 训练模型
model.fit(train_x, train_y)
# 模型预测
results = model.predict(train_x)
print(results)
# 三. 打印结果
for index, sample_result in enumerate(results):
class_tag = "喜欢" if sample_result == "1" else "不喜欢"
print("第 %s 个礼物的特征是%s, %s" % (index, train_x[index], class_tag))
# 生成树结构图
tree.export_graphviz(model, out_file='tree.dot')
# 加载dot文件为graph
(graph, ) = pydot.graph_from_dot_file('tree.dot')
# 可视化树结构
graph.write_png('tree.png')
第 0 个礼物的特征是['1' '1' '0'], 喜欢
第 1 个礼物的特征是['0' '1' '0'], 不喜欢
第 2 个礼物的特征是['1' '0' '0'], 不喜欢
第 3 个礼物的特征是['1' '1' '1'], 喜欢
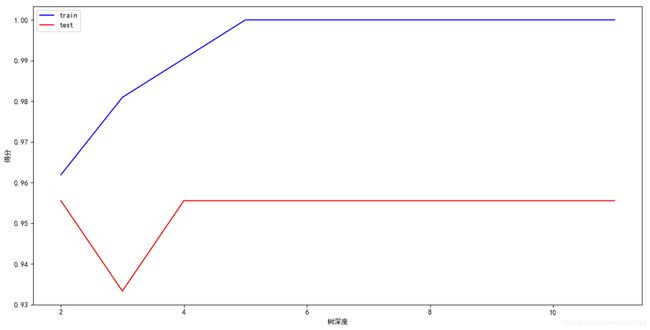
2.超参调优
我们拿鸢尾花数据进行树深度的超参调优:
"""
鸢尾花数据决策树分类超参调优
"""
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt
import pydot
plt.switch_backend("TkAgg")
# 加载鸢尾花数据集
iris = load_iris()
# 做训练集和测试集的划分
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)
# 分别为树深度列表, 训练集得分列表, 测试集得分列表, 用来可视化用
depth = []
train_score = []
test_score = []
for i in range(10):
i += 2
# 分别尝试不同的树深度, 一般来说, 树的深度越深, 越容易过拟合, 但是准确度也会越高
tree_model = tree.DecisionTreeClassifier(criterion="entropy", max_depth=i)
tree_model = tree_model.fit(x_train, y_train)
depth.append(i)
train_score_i = tree_model.score(x_train, y_train)
test_score_i = tree_model.score(x_test, y_test)
train_score.append(train_score_i)
test_score.append(test_score_i)
print("树深度为: %s, 特征重要性: %s, 训练集分数: %.02f, 测试集分数为: %.02f" %
(i, tree_model.feature_importances_, train_score_i, test_score_i))
# 导出.dot文件,里面有树的结构信息
tree.export_graphviz(tree_model, out_file='tree/tree.dot')
# 加载dot文件为 graph
(graph,) = pydot.graph_from_dot_file('tree/tree.dot')
# 将树结构输出为图片
graph.write_png('tree/tree_%s.png' % i)
# 分别绘制曲线图
plt.plot(depth, train_score, color="#0000ff", label="train")
plt.plot(depth, test_score, color="#ff0000", label="test")
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.xlabel('树深度')
plt.ylabel('得分')
# 增加图例
plt.legend()
plt.show()
3.剪枝算法
3.1 预剪枝
a.在构造决策树的同时进行剪枝, 可由参数控制, 比如树的深度, 左右子树个数等
b.所有的决策树都是在无法进一步降低熵的情况下才会停止创建分支,为了避免过拟合, 可以设定一个阈值。熵减小的数量小于这个阈值,即使还可以继续降低熵, 也停止继续创建分支
3.2 后剪枝
a.决策树构造完成后进行剪枝。
b.剪枝的过程是对拥有同样父节点的一组节点进行检查, 判断如果将其合并, 熵的增加量是否小于某一阈值。如果满足阈值要求, 则这一组节点可以合并为一个节点, 其中包含了所有可能的结果。
4.回归树
"""
构建回归树
"""
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import LabelEncoder
import numpy as np
from sklearn import tree
import pydot
# 一. 准备数据
train_x = np.array([["黑色", "贵重", "大"], ["白色", "贵重", "大"], ["黑色", "便宜", "大"], ["黑色", "贵重", "小"]])
train_y = np.array([["喜欢"], ["不喜欢"], ["不喜欢"], ["喜欢"]])
# 将文本数据进行 label encoder 硬编码
train_x[:, 0] = LabelEncoder().fit_transform(train_x[:, 0])
train_x[:, 1] = LabelEncoder().fit_transform(train_x[:, 1])
train_x[:, 2] = LabelEncoder().fit_transform(train_x[:, 2])
train_y[:, 0] = LabelEncoder().fit_transform(train_y[:, 0])
print(train_x)
print(train_y)
# 二. 构建树的分类器
# 构建决策树模型, 树深度设为 10
model = DecisionTreeRegressor(max_depth=10)
# 训练模型
model.fit(train_x, train_y)
# 模型预测
results = model.predict(train_x)
print(results)
# 三. 打印结果
for index, sample_result in enumerate(results):
# 由于是回归问题, 得到的是数字
class_tag = "喜欢" if sample_result == 1 else "不喜欢"
print("第 %s 个礼物的特征是%s, %s" % (index, train_x[index], class_tag))
# 生成树结构图
tree.export_graphviz(model, out_file='tree.dot')
# 加载dot文件为graph
(graph, ) = pydot.graph_from_dot_file('tree.dot')
# 可视化树结构
graph.write_png('tree.png')
第 0 个礼物的特征是['1' '1' '0'], 喜欢
第 1 个礼物的特征是['0' '1' '0'], 不喜欢
第 2 个礼物的特征是['1' '0' '0'], 不喜欢
第 3 个礼物的特征是['1' '1' '1'], 喜欢
三.随机森林
随机森林以随机的方式建立一个森林, 森林里有很多决策树, 且每棵树之间无关联, 当有一个新样本进入后, 让森林中每棵决策树分别各自独立判断, 看这个样本应该属于哪一类, 然后看哪一类被选择最多, 就选择此样本为哪一类。
"""
测试随机森林中决策树个数对评分的影响
"""
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
plt.switch_backend("TkAgg")
iris = load_iris()
train_x = iris['data']
train_y = iris['target']
tree_count = []
scores = []
for i in [1, 3, 6, 9, 10, 20, 50, 100, 200, 1000]:
# 构建随机森林, 设置纯度函数为基尼系数, 最大数深度为10, 树的个数逐渐加大, 并且采用袋外样本评分
# oob即袋外样本(Out Of Bag):在随机森林中,m个训练样本会通过bootstrap (有放回的随机抽样)
# 的抽样方式进行T次抽样, 每次抽样产生样本数为m的采样集,进入到并行的T个决策树中。
# 这样有放回的抽样方式会导致有部分训练集中的样本(约36.8%)未进入决策树的采样集中,
# 而这部分未被采集的的样本就是袋外数据oob。袋外数据就可以用来检测模型的泛化能力, 和交叉验证类似。
clf = RandomForestClassifier(criterion='gini', max_depth=10, n_estimators=i, oob_score=True)
# 在fit之前, 还可以修改参数
# clf.set_params(max_depth=100)
clf.fit(train_x, train_y)
print("树深度: %s, 随机森林评分: %.02f " % (i, clf.oob_score_))
tree_count.append(i)
scores.append(clf.oob_score_)
plt.plot(tree_count, scores)
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.ylabel('评分')
plt.xlabel('决策树个数')
plt.show()
树深度: 1, 随机森林评分: 0.54
树深度: 3, 随机森林评分: 0.84
树深度: 6, 随机森林评分: 0.91
树深度: 9, 随机森林评分: 0.94
树深度: 10, 随机森林评分: 0.92
树深度: 20, 随机森林评分: 0.93
树深度: 50, 随机森林评分: 0.95
树深度: 100, 随机森林评分: 0.95
树深度: 200, 随机森林评分: 0.95
树深度: 1000, 随机森林评分: 0.96
四.Boost算法
随机森林可以缓解决策树过拟合的情况. Boost算法可以缓解欠拟合的情况
Boost算法: 迭代过程中, 新的训练是为了改进上一次的结果。
传统Boost: 对正确、错误的样本进行加权, 每一步结束后, 增加分错点的权重, 减少对分对点的权重。
GradientBoost: 梯度迭代, 每一次建立模型是在之前建立的模型损失函数的梯度下降方向。
1. Adaboost算法
关注被错分的样本, 器重性能好的分类器
不同的训练集 -> 调整样本权重
关注 -> 增加错分样本权重
器重 -> 好的分类器权重大
样本权重间接影响分类器权重
我们看一下 AdaBoost 算法下的回归树分析
"""
AdaBoost 决策树回归分析
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor
plt.switch_backend("TkAgg")
# 创建数据集
# 生成100个 0-6 之间的均匀数字, 并转化为 100 *1 的矩阵
train_x = np.linspace(0, 6, 100)[:, np.newaxis]
# 产生一个随机状态种子, 用来生成伪随机数(即每次生成的随机数都不变, 编号为1)
rng = np.random.RandomState(1)
# 带入到 sin函数中(ravel()是将矩阵拉平, 效果与flatten()相同, 但是flatten()是开辟了新的内存,
# ravel()是基于原矩阵的视图), 并加上均值为0, 方差为0.1的随机数
train_y = np.sin(train_x).ravel() + np.sin(6 * train_x).ravel() + rng.normal(0, 0.1, train_x.shape[0])
print(train_x.shape)
print(train_y.shape)
# 建立普通的回归树
tree_1 = DecisionTreeRegressor(max_depth=4)
tree_1.fit(train_x, train_y)
y_pre_1 = tree_1.predict(train_x)
# 建立 AdaBoost 算法下的随机森林, 树的个数为5
tree_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=5)
tree_2.fit(train_x, train_y)
y_pre_2 = tree_2.predict(train_x)
# 建立 AdaBoost 算法下的随机森林, 树的个数为300
tree_3 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=300)
tree_3.fit(train_x, train_y)
y_pre_3 = tree_3.predict(train_x)
# 开始绘图
plt.figure()
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制图形
plt.scatter(train_x, train_y, c="k", label="样本点")
plt.plot(train_x, y_pre_1, c="g", label="1棵树", linewidth=2)
plt.plot(train_x, y_pre_2, c="r", label="5棵树", linewidth=2)
plt.plot(train_x, y_pre_3, c="b", label="300棵树", linewidth=2)
plt.xlabel("x")
plt.ylabel("y")
plt.title("AdaBoost 决策树回归")
plt.legend()
plt.show()
2. GBDT算法
GBDT(Gradient Boosting Decision Tree) 算法:
用一个初始值来学习一棵决策树,叶子处可以得到预测的值,以及预测之后的残差,然后后面的决策树就要基于前面决策树的残差来学习,直到预测值和真实值的残差为零。
最后对于测试样本的预测值,就是前面许多棵决策树预测值的累加。
使用 XGBoost 做分类或回归问题: XGBoost是一个优化的分布式梯度增强库,旨在实现高效,灵活和便携。它在 Gradient Boosting 框架下实现机器学习算法。将成百上千个分类准确率较低的树模型组合起来,成为一个准确率很高的模型,XGBoost提供并行树提升(也称为GBDT,GBM)
"""
XGBoost并行回归树模型
"""
from sklearn.preprocessing import LabelEncoder
import numpy as np
import xgboost as xgb
# 一. 准备数据
train_x = np.array([["黑色", "贵重", "大"], ["白色", "贵重", "大"], ["黑色", "便宜", "大"], ["黑色", "贵重", "小"]])
train_y = np.array([["喜欢"], ["不喜欢"], ["不喜欢"], ["喜欢"]])
# 将文本数据进行 label encoder 硬编码
train_x[:, 0] = LabelEncoder().fit_transform(train_x[:, 0])
train_x[:, 1] = LabelEncoder().fit_transform(train_x[:, 1])
train_x[:, 2] = LabelEncoder().fit_transform(train_x[:, 2])
train_y[:, 0] = LabelEncoder().fit_transform(train_y[:, 0])
# 二. 构建树的分类器
# 构建 XGBoost 并行回归树模型, 树个数为100, 深度为50
xgb_model = xgb.XGBRegressor(n_estimators=100, max_depth=50)
# 转化为 XGBoost 所需格式, XGBoost要求输入为float32类型
train_x = np.array(train_x).astype(np.float32)
train_y = np.array(train_y.flatten()).astype(np.float32).tolist()
# 训练模型
xgb_model.fit(train_x, train_y)
# 模型预测
results = xgb_model.predict(train_x)
print("真实值: %s, 预测值: %s" % (train_y, results))
# 三. 打印结果
for index, sample_result in enumerate(results):
class_tag = "喜欢" if round(sample_result) == 1 else "不喜欢"
print("第 %s 个礼物的特征是%s, %s" % (index, train_x[index], class_tag))
第 0 个礼物的特征是['1' '1' '0'], 喜欢
第 1 个礼物的特征是['0' '1' '0'], 不喜欢
第 2 个礼物的特征是['1' '0' '0'], 不喜欢
第 3 个礼物的特征是['1' '1' '1'], 喜欢
五.集成学习 Bagging
1.Bagging算法
让某学习算法训练多轮,每轮的训练集由从初始的训练集中随机取出的n个训练样本组成,某个初始训练样本在某轮训练集中可以出现多次或根本不出现,训练之后可得到一个预测函数序列 … ,最终的预测函数H对分类问题采用投票方式,对回归问题采用简单平均。
"""
集成学习 Bagging算法
"""
from sklearn.preprocessing import LabelEncoder
import numpy as np
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
# 一. 准备数据
train_x = np.array([["黑色", "贵重", "大"], ["白色", "贵重", "大"], ["黑色", "便宜", "大"], ["黑色", "贵重", "小"]])
train_y = np.array([["喜欢"], ["不喜欢"], ["不喜欢"], ["喜欢"]])
# 将文本数据进行 label encoder 硬编码
train_x[:, 0] = LabelEncoder().fit_transform(train_x[:, 0])
train_x[:, 1] = LabelEncoder().fit_transform(train_x[:, 1])
train_x[:, 2] = LabelEncoder().fit_transform(train_x[:, 2])
train_y[:, 0] = LabelEncoder().fit_transform(train_y[:, 0])
# 二. 构建树的分类器
# 构建基础模型, 采用KNN算法
base_model = KNeighborsClassifier(n_neighbors=2)
# 将KNN模型套入 BaggingClassifier 中
ensemble_model = BaggingClassifier(base_estimator=base_model, n_estimators=10)
# 将 train_y 拉平
train_y = np.array(train_y.flatten())
# 开始训练
ensemble_model.fit(train_x, train_y)
results = ensemble_model.predict(train_x)
print("真实值: %s, 预测值: %s" % (train_y, results))
# 三. 打印结果
for index, sample_result in enumerate(results):
class_tag = "喜欢" if sample_result == "1" else "不喜欢"
print("第 %s 个礼物的特征是%s, %s" % (index, train_x[index], class_tag))
真实值: ['1' '0' '0' '1'], 预测值: ['1' '0' '0' '1']
第 0 个礼物的特征是['1' '1' '0'], 喜欢
第 1 个礼物的特征是['0' '1' '0'], 不喜欢
第 2 个礼物的特征是['1' '0' '0'], 不喜欢
第 3 个礼物的特征是['1' '1' '1'], 喜欢
2.集成学习Boosting
初始化时对每一个训练例赋相等的权重/, 然后用该学算法对训练集训练t轮, 每次训练后, 对训练失败的训练例赋以较大的权重, 也就是让学习算法在后续的学习中集中对比较难的训练例进行学习,从而得到一个预测函数序列 … , 其中也有一定的权重,预测效果好的预测函数权重较大,反之较小。最终的预测函数H对分类问题采用有权重的投票方式,对回归问题采用加权平均的方法对新示例进行判别。
"""
集成学习 Boosting 算法
"""
from sklearn.ensemble import AdaBoostClassifier
from sklearn.linear_model.logistic import LogisticRegression
# 一. 准备数据
train_x = [[1, 0, 1], [0, 0, 1], [1, 1, 1], [1, 0, 0]]
# 0代表喜欢,1代表不喜欢
train_y = [0, 1, 1, 0]
# 二. 构建树的分类器
# 构建基础模型, 采用 逻辑回归 算法
base_model = LogisticRegression()
# 将逻辑回归模型套入 BaggingClassifier 中
ensemble_model = AdaBoostClassifier(base_estimator=base_model, n_estimators=10)
ensemble_model.fit(train_x, train_y)
results = ensemble_model.predict(train_x)
print("真实值: %s, 预测值: %s" % (train_y, results))
真实值: [0, 1, 1, 0], 预测值: [0 1 1 0]
3.集成学习 Stacking
将训练好的所有基模型对训练基进行预测,第个基模型对第个训练样本的预测值将作为新的训练集中第个样本的第个特征值,最后基于新的训练集进行训练。同理,预测的过程也要先经过所有基型的预测形成新的测试集,最后再对测试集进行预测。
"""
集成学习 voting/stacking算法
"""
from sklearn.preprocessing import LabelEncoder
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.tree.tree import DecisionTreeClassifier
# 一. 准备数据
train_x = np.array([["黑色", "贵重", "大"], ["白色", "贵重", "大"], ["黑色", "便宜", "大"], ["黑色", "贵重", "小"]])
train_y = np.array([["喜欢"], ["不喜欢"], ["不喜欢"], ["喜欢"]])
# 将文本数据进行 label encoder 硬编码
train_x[:, 0] = LabelEncoder().fit_transform(train_x[:, 0])
train_x[:, 1] = LabelEncoder().fit_transform(train_x[:, 1])
train_x[:, 2] = LabelEncoder().fit_transform(train_x[:, 2])
train_y[:, 0] = LabelEncoder().fit_transform(train_y[:, 0])
# 二. 构建树的分类器
# 构建knn算法模型
knn_model = KNeighborsClassifier(n_neighbors=1)
# 构建决策树模型
tree_model = DecisionTreeClassifier(max_depth=10)
# 模型融合
models_list = [("model_knn", knn_model), ("tree_model", tree_model)]
voting = VotingClassifier(estimators=models_list)
# 将 train_y 拉平
train_y = np.array(train_y.flatten())
# 开始训练
voting.fit(train_x, train_y)
results = voting.predict(train_x)
print("真实值: %s, 预测值: %s" % (train_y, results))
# 三. 打印结果
for index, sample_result in enumerate(results):
class_tag = "喜欢" if sample_result == "1" else "不喜欢"
print("第 %s 个礼物的特征是%s, %s" % (index, train_x[index], class_tag))