【ElasticSearch 进阶】倒排索引 + FOR + RBM压缩算法
1. 倒排索引
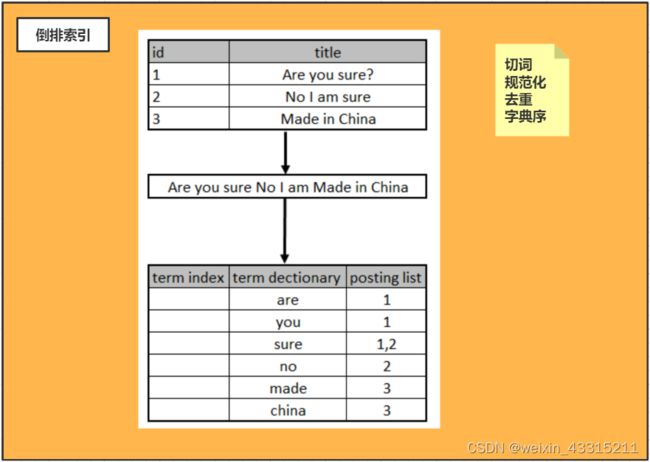
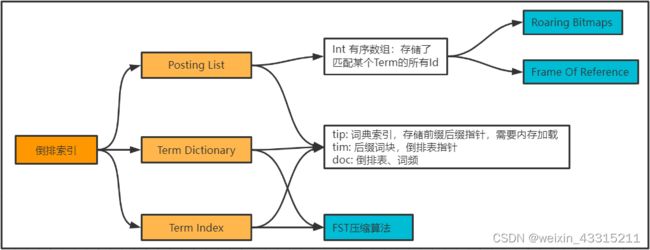
如果有100w的数据,进行分词后,每个id按数字类型进行存储,假设每个行数据都包含相同的词,则每个词的 Posting List 需要占用约4M的空间:
1 int = 4 Bytes
100W int = 400W Bytes ≈ 4M
极大的浪费了空间。则需要对Posting List 进行压缩,压缩算法有:FOR + RBM
2. FOR压缩算法
FOR算法的核心思想是用减法来削减数值大小,从而达到降低空间存储。
假设V(n)表示数组中第n个字段的值,那么经过FOR算法压缩的数值V(n)=V(n)-V(n-1)。也就是说存储的是后一位减去前一位的差值。存储是也不再按照int来计算了,而是看这个数组的最大值需要占用多少bit来计算,如例所示:
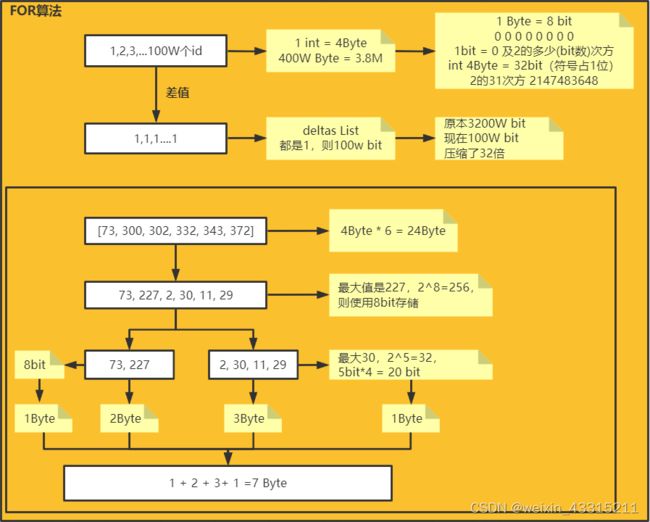
例一:
- 比如Posting List是1-100W的有序数组,原本需要4Byte * 100W =3200W bit
- 压缩后的Delta List全是1的数组,100W bit,直接压缩了32倍
例二
- 比如数组是73,300,302,332,342,372,原本需要4 * 6 byte = 24byte = 192bit
- 压缩后:73,227,2,30,11,29,其中227最大,需要 8bit 的容器来存放,共计需要 8 * 6 = 48 bit,还需要记录容器的记录,需要1Byte,则 48 + 8 = 56bit
- 继续观察这个数组,发现最大值227和最小值2,相差较大,因为2只需要1bit来存放,比较浪费,所以还可以对数据进行分组:[73, 227] [2, 30, 11, 29 ]
- 分组后占用空间就变成了 [73, 227] 还是需要 8bit 的空间,但 [2, 30, 11, 29 ]最大值是30 < 2^5,只需要 5bit 的空间,因此总空间 8bit * 2 + 5bit * 4 + 2 * 8bit =52 bit
可以看到大小又变小了,但是思考一个问题:是不是还可以进行压缩?是越小越好吗?
是可以再压缩,但是我们还要考虑解码的问题,数据压缩后是要使用的,因此需要解码,压缩得越深,解码越耗时,并且存放容器记录也需要占用空间,因此不是越小越好,那么在哪里取一个平衡,这就是通过计算机动态计算。
- 数组元素值为与前一位的差值V(n)=V(n)-V(n-1),n=2,3,4…
- 稠密数组
- 计算数组中最大值所需占用的大小
- 计算数组是否需要拆分,计算拆分后每组的最大值所需占用的大小并记录
3. RBM压缩算法
FOR算法的核心是用减法来缩减数值大小,但数值太过离散时,减法能够达到的效果是不明显的,比如100W,200W,300W,相减后是100W,100W,100W,依然很大,这时的压缩效果很不理想,所以引入了RBM算法。
更有效减小数值的大小的方法:除法
RBM的核心就是通过除法来缩减数值大小,但是并不是直接的相除。
比如数组为 [1000, 62101, 131385, 191173, 196658]
其中196658的二进制表示为0000 0000 0000 0011 0000 0000 0011 0010
然后将其高16位和低16位分别转换为10进制:
0000 0000 0000 0011 -> 3
0000 0000 0011 0010 -> 50
那么196658就转换成了(3,50)的表示形式,其效果就相当于除以2^16(因为int类型的最大值就是 2 ^32 = 2^16 * 2^16),商3余50
再因为商和余数都不超过16位,那么我们最大用16bit来存储足够了。也就是short类型,因此商和余数都可以用一个short来盛装。
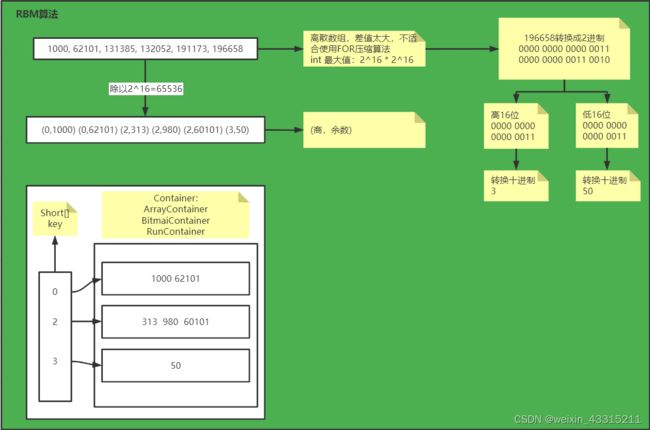
将每一个商所对应的余数short[]称之为一个容器Container,使用上述所说的short盛装也称为ArrayContainer。
现在有10亿条11位的电话号码,请问如何用2G的空间将他们存储下来?
答:使用数组
存储电话号码phone: arr[(phone-10000000000)/64] | (1 << ((phone-10000000000)%64))
判断电话号码是否存在:arr[(phone-10000000000)/64] & (1 << ((phone-10000000000)%64)) > 0
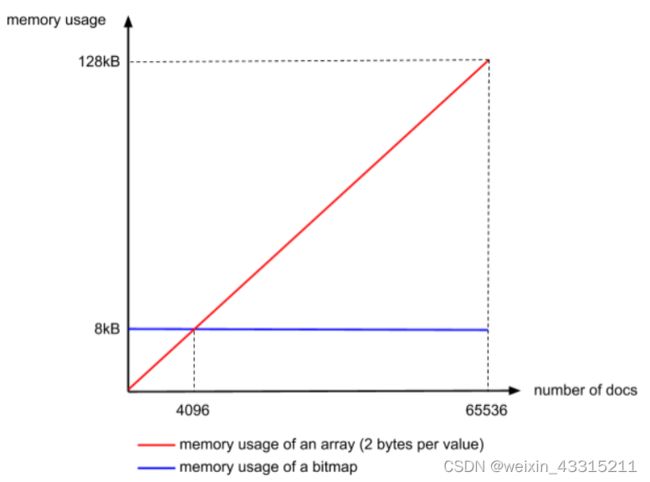
以上的二维数组,每一个Container中的数据当量足够多时我们认为他是有序连续的,就可以选用bitmap来进行存储,按照规定一个Container的最大值是65534,也就需要65535bit=8k的容器来存储,当然bitmap有个很明显的缺点,那就是无论Container中有多少个数,都要占用8k的大小,所以当数量不超过65535bit /16bit = 4096个时,使用short (16bit)来存储更划算,当每个Container的数量超过4096个时使用bitmap更加划算,那么使用bitmap的Container称为BitmapContainer
还有一个Container叫RunContainer,专门用来解决连续数组存储的,比如[1,2,3,100W],那么可以表示为[1,100W],只存储一个最小值和最大值,如果数组是如下形式
[1,2,3,4,5,100,101,102,999,1000,1001]
就会被拆分为三段:[1,5],[100,102],[999,1001]