知识表示学习与图嵌入综述
文章目录
- 一、任务的介绍与背景
-
- 1.1 表示空间
- 1.2 打分函数
- 1.3 编码模型
- 1.4 结合辅助信息
- 1.5 图表示学习
- 二、典型方法
- 三、各方法综述和性能比较
-
- 3.1 基于矩阵特征向量计算
- 3.2 基于随机游走的方法
- 3.3 基于深度学习的方法
- 3.4 保存特殊性质的网络表示
- 3.5 基于翻译模型(Trans系列)的知识表示学习
- 3.6 图卷积网络在关系抽取的作用
- 四、图嵌入相关数据集及方法比较
- 五、结论
- 六、知识图谱表示结合图嵌入应用的未来方向
- 参考文献
一、任务的介绍与背景
知识图谱表示学习对于知识获取和下游应用具有很重要的作用. 知识表示学习的表示空间包括:point-wise空间,流形空间,复数空间,高斯分布和离散空间. 打分函数通常分为基于距离的打分和基于语义匹配的打分函数. 编码模型包括:线性/双线性模型,张量分解和神经网络. 辅助信息考虑文本,视觉和类型信息.
1.1 表示空间
1.1.1 Point-wise空间
Point-wise的欧式空间是最常用的,将知识图谱中的实体和关系嵌入为向量或者矩阵空间,也有的捕捉关系交互. Point-wise方法包括基于翻译的方法TransE,需要满足平移不变特性h + r = t、TransR、TransH,也有语义匹配的方法NTN、HolE、ANALOGY.
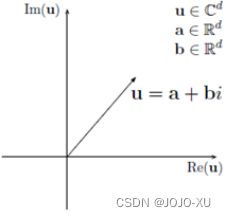
1.1.2 复数向量空间
从实数空间扩展到复数空间可以得到更多一维的实体和关系表示,具有更丰富的表示能力. ComplEx是第一个将知识图谱表示学习扩展到复数空间的,其中,使用哈密顿乘积法组合多个关系,这种方法可以建模对称和反对称关系. RotatE利用哈密顿乘法将关系视为从头实体到尾实体的旋转操作. QuatE将复数空间扩展到了四元数空间,包含三个虚部和一个实部,通过四元数乘法例如哈密顿乘法组合头实体和关系.
1.1.3 高斯分布
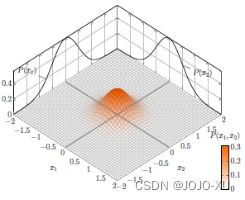
由高斯词嵌入方法得到的启发,KG2E模型将实体和关系嵌入多维高斯分布,均值向量表示实体和关系的位置,方差矩阵建模了不确定性. TransG表示具有高斯分布的实体,同时给出了对于关系嵌入的混合高斯分布.
1.1.4 流形和群
流形是一种拓扑空间,可以用集合论将其定义为具有邻域的一组点,而该组是抽象代数中定义的代数结构. 先前的point-wise建模是一个不适定的代数系统,而ManifoldE将point-wise嵌入扩展为基于流形的嵌入,并介绍了基于流形嵌入的两种设置,即球面和超平面.
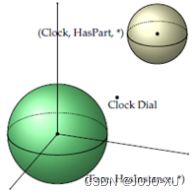
基于球面的方法需要将实体和关系从原始空间映射到希尔伯特空间,形式如下公式所示:
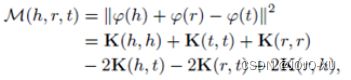
TorusE通过将实体和关系嵌入在一个紧凑的Lie群的n维环面空间中,并根据TransE的翻译思想h + r = t来学习嵌入表示.
1.2 打分函数
打分函数用来衡量一个三元组成立的可靠程度,有时也被称为能量函数,是基于能量的学习框架的基础. 基于能量学习的目标是保证正样本的打分高于负样本的打分(在TransE中,是负样本打分高于正样本打分,这个我认为主要看如何定义这个打分函数). 打分函数通常分为两种情况:基于距离的打分函数和基于语义匹配的打分函数.
(1) 基于距离的打分函数通过衡量两个实体之间的距离的可靠程度,这里是使用关系作为加性的平移操作,类似于TransE定义的h + r = t.
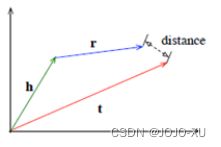
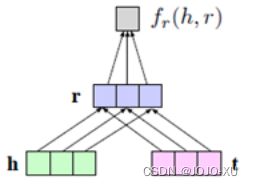
(2) 基于语义匹配的打分函数通过头实体向量和关系矩阵的乘性计算,使得头实体与关系组合后转移到尾实体附近h_Mr = t
1.3 编码模型
通过特定的模型结构能够对实体和关系之间的交互进行编码,包括线性/双线性模型、张量分解模型和神经网络模型.
1.3.1 张量分解模型
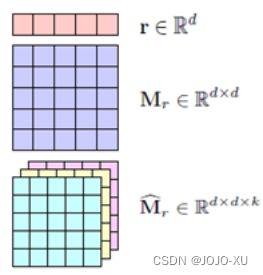
张量分解模型的基本思想是将一个三阶张量中每个切片的矩阵分解为在低维空间的两个实体向量与关系矩阵的乘积. 在RESCAL模型中,对于一个具有总共m个关系的知识图谱,其第k个关系对应的表示这个关系的所有实体间关联关系的切片可以分解为:
![]()
LFM对RESCAL通过一个双线性结构进行分解:
![]()
1.3.2 Transformer
Transformer在NLP里尤其是以Bert为代表的自然语言预训练中已经成为炙手可热的一项技术,基于Transformer的表示学习可以集成知识图谱中的上下文信息. CoKE使用Transformer来编码边和路径序列. KG-BERT从预训练语言模型中得到启发,采用Transformer来编码实体和关系.
1.3.3 图神经网络
GNN可以在一个encoder-decoder框架下学习连接结构信息. RGCN提出了关系特定的转换,以建模知识图谱的有向性. 在第l+1层得到的聚合一个实体的邻域信息的状态为:

这里,GCN是一个编码器,针对不同任务可以选择不同的编码器集成到RGCN这个框架中. 由于RGCN将每个实体的邻域信息都等价对待
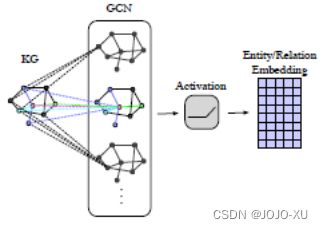
SACN设计了带有权重的GCN,定义了相同关系类型下两个邻接的节点连接强度. 解码器模块通常使用ConvE来作为语义匹配的度量,使用C个卷积核,可以得到实体和关系嵌入表示的卷积输出为:
![]()
接着,打分函数设计为:
![]()
KBAT模型通过拼接实体和关系嵌入表示,然后采用图注意力网络和多头注意力机制来编码多跳邻域信息.
1.4 结合辅助信息
为了进一步提高表示学习的性能,结合一些外部辅助信息可以实现多模态嵌入,包括文本描述,类型约束,关系路径,视觉信息与,逻辑规则等和知识图谱本身进行结合.
1.4.1 文本描述
知识图谱中的实体描述信息可以补充语义信息. 结合文本描述的知识表示学习的挑战在于如何将结构化的知识图谱和非结构化的文本描述嵌入在同一个表示空间中. 一种方法是通过引入实体名称和Wikipedia的集合,用对齐模型来对齐实体空间和词空间. DKRL对TransE进行扩展,利用CNN学习实体描述的表示. SSP将三元组和文本描述映射到一个语义空间中,并用一个关于嵌入的loss和一个关于主题的loss组成整体loss.
1.4.2 类型信息
知识图谱中的实体有时会带有层次化的类别或类型信心. SSE模型结合实体类型来对属于同一类型的实体进行嵌入. TKRL通过关于实体类型的映射矩阵来捕捉层次化类型信息. KR-EAR将关系类型分为属性和关系,并建模了实体描述之间的关联.
1.4.3 视觉信息
视觉信息例如实体的图片也能够用来增强知识表示学习. IKRL将图像编码到实体空间,确保基于三元组结构化的表示和基于图像的表示处于同一表示空间中,并遵循平移不变原理学习实体和关系的嵌入表示.
1.5 图表示学习
对于网络科学而言,世间万物都可以抽象成点,而事物之间的关系都可以抽象成边,并根据不同的应用场景,生成不同的网络,因此整个世界都可以用一个巨大的复杂网络来代表. 常用的图有社交关系网络、商品网络、知识图谱等.
网络数据形式可以自然地表达物体和物体间的联系, 在我们的日常生活与工作中无处不在. 举例来说, Facebook和新浪微博等构成了人与人之间的社交网络; 互联网上成千上万个页面构成了网页链接的网络; 国家城市间的运输交通构成了物流网络. 由此可见, 信息网络是我们生产生活中最为常见的一种信息载体和形式. 信息社会中很多网络节点拥有丰富的文本等外部信息, 形成典型的复杂信息网络. 基于复杂信息网络的广泛存在, 对这类网络信息进行研究与分析具有非常高的学术价值和潜在应用价值. 对于复杂信息网络的分析, 根据信息网络载体的不同, 也会具有非常广的普适性. 对于网格化数据(grid-like data)的分析已经取得相当瞩目的进展,但对于复杂的网络结构数据的研究仍然处于非常初级的阶段 [19, 20].
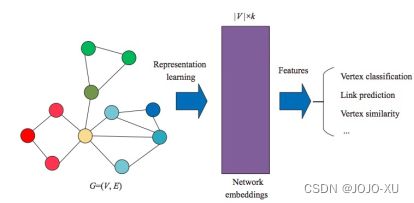
对于图结构数据的研究,一个根本的问题在于如何恰当地表示出图中蕴含的信息.传统的方法将图结构的数据表示为一个高维稀疏矩阵(如使用图的邻接矩阵),但是对这一矩阵进行分析将耗费大量的时间与空间成本,且不能较好地编码图中节点的结构信息.举例来说,社交网络中的链接预测任务中,需要编码出图中节点对之间的关系(如共同拥有的好友数、关系强弱等). 传统的方法通常无法直接地对 上述信息进行编码,而是采用统计方法(如计算度矩阵(degree matrix)、聚类系数(clustering coefficients)等)[1]、核函数(kernel functions)[2] 或特征工程(feature engineering)[3] 的方法对图中节点的局部结构进行度量.然而,传统的方法具有严重的局限性,因为这些传统的方法通常需要花费大量时间与人力在设计特征上,并且这些设计出来的特征并不能随着学习过程进行调整.
图表示学习的过程主要被分为两个部分:编码器(encoder)与解码器(decoder),如图 1 所示.编码器用于将图中的每个节点映射为一个向量,而解码器 则将节点嵌入向量中下游任务关心的信息提取出来,比如提取出节点的分类标签或 者结构信息.通过对编码器与解码器进行联合训练(joint train),整个系统即可学习到如何将图数据中的结构信息压缩到一个嵌入空间中.图 2 展示了一个使用 DeepWalk[4] 算法对空手道俱乐部社交网络数据集[5] 进行节点嵌入的例子.
Graph Embedding 是一种将复杂网络投影到低维空间的机器学习技术,典型的做法是将网络中的节点做向量化表达,使节点间的向量相似度接近原始节点间在网络结构、近邻关系、Meta信息等多维度上的相似性.
Graph Embedding的基本做法是,对graph进行采样(Sampling),采出来的序构建模型(Embedding). 一个典型的方法是将语言模型和无监督学习从单词序列扩展到图结构上,将截断游走的序列当成句子进行学习,之后采用word2vec中Skip-Gram模型进行训练,得到每个节点的embedding向量.

图 10 对空手道俱乐部社交网络数据集中的节点进行嵌入.图中节点的标号为节点序号,节点的颜色表示根据模块度(modularity)进行聚类得到 的分类标签.右图代表使用图嵌入算法将每个节点映射为一个二维嵌入向 量.请注意左图中的社区结构与节点嵌入向量之间的对应关系:通过最大 化模块度找到的社区结构(由顶点颜色代表)在节点嵌入向量中得到了保 留,这些结构相似节点的嵌入向量在嵌入空间中仍然形成簇.
关于Embedding
为什么要用Embedding层?
- ·使用One-hot 方法编码的向量会很高维也很稀疏.
- ·除此之外无法学习词与词之间的相似性.如图11所示:

图11 one-hoe编码
而embedding层可以把词转换为词向量,在低维稠密的连续实数空间表达,从图12可以看到,相似的词之间的距离比较近.其中这个转换后词向量的维度是自己定义的.可以做超参数调节.
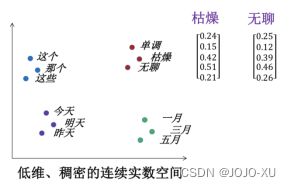
图12 词向量
这些词向量是神经网络的输入.
二、典型方法
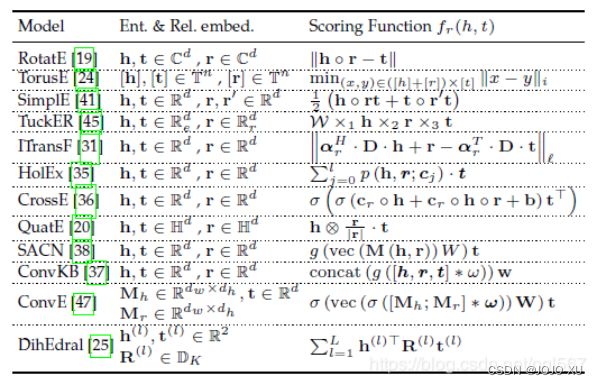
最近几年最前沿的知识表示学习模型如下表所示[32]:
基于翻译模型(Trans系列)的知识表示学习单独介绍,见3.5节.
在过去的十年里,在图形嵌入领域已经有了大量的研究,重点是设计新的嵌入算法.发展到现在,大体上可以将这些嵌入方法分为四大类:( 1 ) 基于矩阵特征向量计算的方法,( 2 )基于随机游走的方法,( 3 )基于深度学习的方法以及( 4 )保存特殊性质的网络表示的方法. 在下文中我将简要解释每一个类别的特征与每一类别代表性算法的原理.
三、各方法综述和性能比较
3.1 基于矩阵特征向量计算
较早的用于网络表示学习的算法主要归于此类. 谱聚类算法通过计算关系矩阵的前 k 个特征向量或奇异向量来得到 k 维的节点表示. 关系矩阵一般就是网络的邻接矩阵或者 Laplace 矩阵. 这类方法强烈的依赖于关系矩阵的构建, 不同的关系矩阵的评测结果差异很大. 一般来讲, 基于谱聚类方法的时间复杂度较高, 因为特征向量和奇异向量的计算时间是非线性的. 另一方面, 谱聚类方法需要将关系矩阵整体存于内存之中, 所以空间复杂度也是不能忽略的. 这些局限性阻止了这类算法在大规模数据和在线平台上的扩展应用. 现在将展示几种谱聚类算法的实例. 这些方法的适用性如表 1 所示. 局部线性表示 (locally linear embedding) [6, 7] 假设节点的表示是从同一个流形中采样得到的. 局部线性表示假设一个节点和它邻居的表示都位于该流形的一个局部线性的区域. 也就是说, 一个节点的表示可以通过它的邻居节点的表示的线性组合来近似得到. 局部线性表示使用邻居节点表示的加权和与中心节点表示的距离作为损失函数. 最小化损失函数的优化问题最终转化成某个关系矩阵特征向量计算问题求解.
Laplace 特征表 (Laplace eigenmap) [8, 9] 简单的假设两个相连的节点的表示应该相近. 特别地, 这里表示相近是由向量表示的欧氏距离的平方来定义. 该优化问题可以类似地转化为 Laplace 矩阵的特征向量计算问题.
有向图表示 (directed graph embedding) [10] 进一步扩展了 Laplace 特征表方法, 给不同点的损失函数以不同的权重. 其中点的权重是由基于随机游走的排序方法来决定, 如 PageRank.
3.2 基于随机游走的方法
3.2.1 DeepWalk
DeepWalk方法受到word2vec的启发,首先选择某一特定点为起始点,做随机游走得到点的序列,然后将这个得到的序列视为句子,用word2vec来学习,得到该点的表示向量.DeepWalk通过随机游走去可以获图中点的局部上下文信息,因此学到的表示向量反映的是该点在图中的局部结构,两个点在图中共有的邻近点(或者高阶邻近点)越多,则对应的两个向量之间的距离就越短.
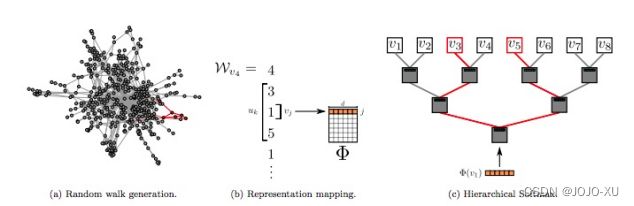
图13 DeepWalk概述.我们在随机游走Wv4上滑动一个长度为2w +1的窗口,将中心顶点v1映射为其表示Φ(v1). Softmax分层结构在概率分布序列上分解出Pr(v3 |Φ(v1))和Pr(v5 |Φ(v1)),这些概率分布对应于从根开始并在v3和v5结束的路径. 更新表示Φ以最大化v1与其上下文{v3,v5}同时出现的可能性.
3.2.2 node2vec
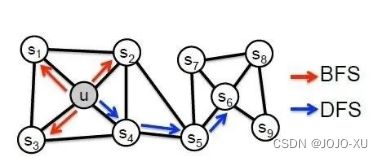
与DeepWalk相似,node2vec通过最大化随机游走得到的序列中的节点出现的概率来保持节点之间的高阶邻近性.与DeepWalk的最大区别在于,node2vec采用有偏随机游走,在广度优先(bfs)和深度优先(dfs)图搜索之间进行权衡,从而产生比DeepWalk更高质量和更多信息量的嵌入.
3.3 基于深度学习的方法
3.3.1 Structural deep network embedding (SDNE)
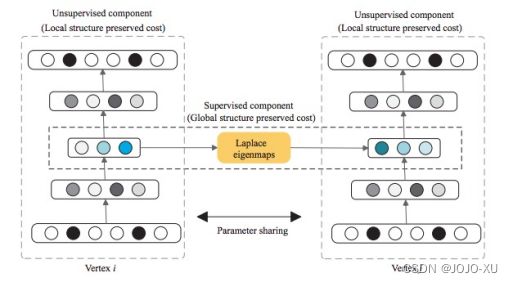
SDNE建议使用深度自动编码器来保持一阶和二阶网络邻近度.它通过联合优化这两个近似值来实现这一点.该方法利用高度非线性函数来获得嵌入.模型由两部分组成:无监督和监督.前者包括一个自动编码器,目的是寻找一个可以重构其邻域的节点的嵌入.后者基于拉普拉斯特征映射,当相似顶点在嵌入空间中彼此映射得很远时,该特征映射会受到惩罚.
3.3.2 Deep neural networks for learning graph representations (DNGR)
DNGR结合了随机游走和深度自动编码器.该模型由3部分组成:随机游走、正点互信息(PPMI)计算和叠加去噪自编码器.在输入图上使用随机游走模型生成概率共现矩阵,类似于HOPE中的相似矩阵.将该矩阵转化为PPMI矩阵,输入到叠加去噪自动编码器中得到嵌入.输入PPMI矩阵保证了自动编码器模型能够捕获更高阶的近似度.此外,使用叠加去噪自动编码器有助于模型在图中存在噪声时的鲁棒性,以及捕获任务(如链路预测和节点分类)所需的底层结构.
3.3.3 Graph convolutional networks (GCN)
上面讨论的基于深度神经网络的方法,即SDNE和DNGR,以每个节点的全局邻域(一行DNGR的PPMI和SDNE的邻接矩阵)作为输入.对于大型稀疏图来说,这可能是一种计算代价很高且不适用的方法.图卷积网络(GCN)通过在图上定义卷积算子来解决这个问题.该模型迭代地聚合了节点的邻域嵌入,并使用在前一次迭代中获得的嵌入及其嵌入的函数来获得新的嵌入.仅局部邻域的聚合嵌入使其具有可扩展性,并且多次迭代允许学习嵌入一个节点来描述全局邻域.最近几篇论文提出了利用图上的卷积来获得半监督嵌入的方法,这种方法可以通过为每个节点定义唯一的标签来获得无监督嵌入.这些方法在卷积滤波器的构造上各不相同,卷积滤波器可大致分为空间滤波器和谱滤波器.空间滤波器直接作用于原始图和邻接矩阵,而谱滤波器作用于拉普拉斯图的谱.
3.3.4 Variational graph auto-encoders (VGAE)
VGAE采用了图形卷积网络(GCN)编码器和内积译码器.输入是邻接矩阵,它们依赖于GCN来学习节点之间的高阶依赖关系.他们的经验表明,与非概率自编码器相比,使用变分自编码器可以提高性能.
3.4 保存特殊性质的网络表示
使用向量表示代替原始网络的策略在带来便利的同时, 也会丢失很多原始网络中的信息. 比如大多数网络表示学习方法使用向量表示间的内积或者余弦距离刻画节点相似度. 但内积或者余弦距离都是无向的, 会丢失网络中的非对称性. 另一方面, 一些依赖于网络结构定义的性质, 如社区 (community)等信息, 也会在网络表示学习的过程中丢失.
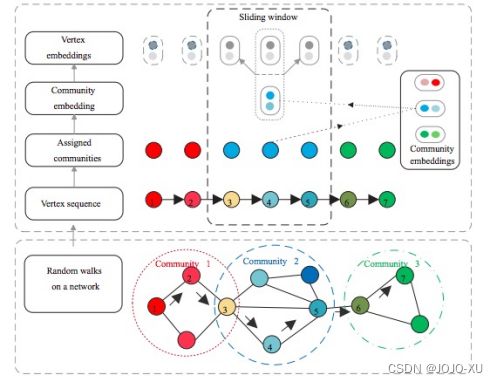
HOPE 算法为每个节点刻画了两种不同的表示, 并着眼于保存原始网络中的非对称性信息. HOPE 构建了不同的非对称的关系矩阵, 然后使用 JDGSVD 算法进行矩阵降维得到节点的网络表示. CNRL 算法 [11] 考虑了在节点表示中嵌入网络隐藏的社区信息. 如图 8 所示, CNRL 假设每个节点属于多个社区, 也就是每个节点在所有的社区上有一个概率分布. DeepWalk 将随机游走生成的节点序列看作句子, 将序列中的节点看作文本中的词, 直接用训练词向量的 Skip-Gram 模型来训练节点向量. 受这种类比的启发, CNRL 将网络中的社区看作文本中的主题, 也就是说, 网络中相关的节点倾向于行程社区, 而文本中相关的词则会构成主题. 因此, CNRL 算法在生成的随机游走序列上, 将每个节点序列看成一篇文档, 通过基于 Gibbs 采样的 LDA [12] 来学习每个节点的社区分布, 并通过随机采样的方式, 来给序列中的节点分配其对应的社区标签. 随后, 在 Skip-Gram 模型的基础上, 用中心节点的节点表示和对应的社区表示同时去预测随机游走序列中的邻近节点, 从而将社区结构信息保存在节点表示中. 为了对通过主题模型检测出的社区有一个直观的感受, 验证将网络中的社区类比为文本中的主题的正确性, CNRL 对一个小的 Karate 网络进行了社区发现结果的可视化, 如图 9 所示. 可以发现, CNRL 能够有效检测出不同规模的有重叠的社区, 以及有效的识别出社区边界.
3.5 基于翻译模型(Trans系列)的知识表示学习
3.5.1 TransE: 多元关系数据嵌入
这篇文章提出了一种将实体与关系嵌入到低维向量空间中的简单模型,弥补了传统方法训练复杂、不易拓展的缺点,对实体和关系的建模十分简单明了,可解释性也很强. 尽管现在还不清楚是否所有的关系种类都可以被这种方法建模,但目前这种方法相对于其他方法表现不错.在后续的研究中,TransE更是作为知识库vector化的基础,衍生出来了很多变体.
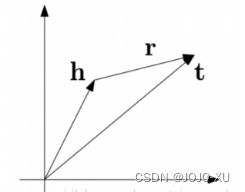
受word2vec启发,利用了词向量的平移不变现象.将每个三元组实例 (head,relation,tail) 中的关系 relation 看做从实体 head 到实体 tail 的翻译,通过不断调整h、r和t (head、relation 和 tail 的向量),使 (h + r) 尽可能与 t 相等,即 h + r ≈ t.其损失函数表示如下:

3.5.2 TransR: 实体和关系分开嵌入
问题:一个实体是多种属性的综合体,不同关系关注实体的不同属性.直觉上一些相似的实体在实体空间中应该彼此靠近,但是同样地,在一些特定的不同的方面在对应的关系空间中应该彼此远离.
方案:将实体和关系嵌入到不同的空间中,在对应的关系空间中实现翻译.

TransR在TranE的基础上的改进,在数学上的描述看起来会更加直观:对于每一类关系,不光有一个向量rr来描述它自身,还有一个映射矩阵MrMr来描述这个关系所处的关系空间.
3.5.3 TransD: 通过动态映射矩阵嵌入
问题:TransR过于复杂,在TransR的基础上减少参数…
方案:实体和关系映射到不同的空间中,用两个向量表示实体或关系,一个(h,r,t)表征实体或关系,另一个 (hp,rp,tp)用来构造动态映射矩阵.
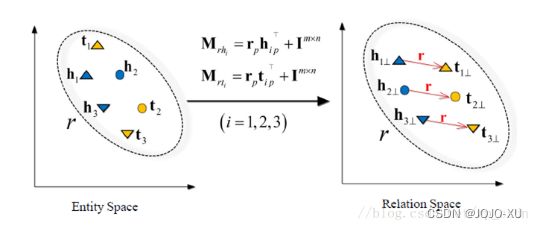
TransD在TransR的基础上,将关系的映射矩阵简化为两个向量的积,图中M_rh与M_rt表示实体h与实体r映射到关系空间的矩阵.
3.6 图卷积网络在关系抽取的作用
关系抽取是从纯文本中提取未知关系事实并将其加入到知识图谱中,是自动构建大规模知识图谱的关键. 由于缺少标记的关系数据,远程监控(distance supervision)也称为弱监控或自监督,通过假设包含相同实体的语句在关系数据库的监督下可以表示相同的关系,使用启发式匹配来创建训练数据. Mintz等人采用了远程监控的关系分类方法,文本特征包括词汇和句法特征、命名实体标记和连接特征. 传统方法高度依赖于特征工程,最近一种方法探索了特征之间的内在关联. 深度学习正在改变知识图谱和文本的表示学习.
GCN用于对句子的依赖树进行编码,或者学习知识图谱嵌入以利用关系知识进行句子编码. C-GCN是以路径为中心的句子剪枝依赖树上的上下文GCN模型. AGGCN也对依赖树应用GCN,但以软加权的方式利用多头注意力进行边缘选择. 与前两种基于GCN的模型不同,Zhang等人将GCN应用于知识图谱中的关系嵌入,用于基于句子的关系抽取. 进一步提出了一种粗到细的知识感知注意力机制,用于信息实例的选择.
四、图嵌入相关数据集及方法比较
SYN-SBM:具有1024个节点和3个社区的随机块模型[13]生成合成图.可以使用它来可视化通过各种方法学习到的嵌入.
KARATE [14]:Zachary的空手道网络是大学空手道俱乐部的知名社交网络.在社交网络分析中已经进行了广泛的研究.该网络有34个节点,78个边缘和2个社区.
BLOGCATALOG [15]:这是BlogCatalog网站上列出的博客作者的社交关系网络.标签代表通过博客提供的元数据推断出的博客兴趣.该网络有10,312个节点,333,983个边缘和39个不同的标签.
YOUTUBE [16]:这是Youtube用户的社交网络.这是一个大型网络,包含1,157,827个节点和4,945,382个边缘.标签代表喜欢常见视频流派的用户组.
HEP-TH [17]:原始数据集包含1993年1月至2003年4月期间发表的《高能物理理论》论文的摘要.这是为该时期发表的论文创建的一个协作网络.该网络有7,980个节点和21,036个边缘.
ASTRO-PH [18]:这是一个由1993年1月至2003年4月期间提交给e-print arXiv的论文的作者组成的协作网络.该网络具有18,772个节点和396,160个边.
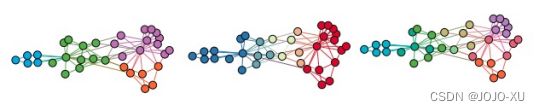
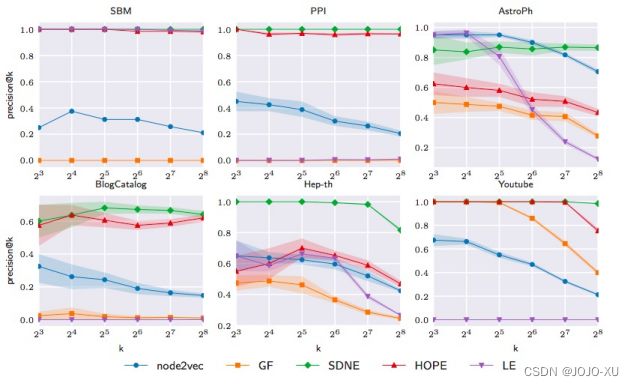
SBM的可视化如图21所示.众所周知的底层社区结构,我们使用社区标签为节点着色. 我们观察到,尽管数据结构良好,LE,GF和LLE可以在一定程度上捕获社区结构,但是HOPE和SDNE生成的嵌入保留了较高级别的邻近性,从而很好地分隔了社区.

图22说明了通过128维嵌入获得的重构精度. 我们观察到,尽管方法的性能取决于数据集,但通常保留较高阶邻近度的嵌入方法要优于其他方法. 拉普拉斯特征图在SBM上的出色表现可以归因于数据集中缺少更高阶的结构. 我们还观察到SDNE在所有数据集上始终表现良好. 这可以归因于其从网络中学习复杂结构的能力. node2vec学习到的嵌入具有较低的重构精度. 这可能是由于高度非线性的降维导致了非线性流形. 但是,希望学习线性嵌入但保留较高阶接近度的HOPE可以很好地重建图形,而无需任何其他参数.
五、结论
最流行的表示空间是基于欧氏空间,通过将实体嵌入向量空间并通过向量,矩阵或张量建模实体间的交互. 其它表示空间包括复数向量空间,高斯分布以及流形空间和群. 流形空间比点式欧式空间具有的优势是可以放宽点式嵌入. 高斯嵌入能够表示实体和关系的不确定性以及多重关系的语义. 嵌入复数向量空间可以有效地建模不同的关系连通性模式,尤其是对称/反对称模式. 表示空间在编码实体的语义信息和捕获关系属性方面起着重要作用. 在设计表示学习模型时,应仔细选择和设计适当的表示空间,以匹配编码方法的性质,并平衡表示能力和计算复杂性. 基于距离的度量的打分函数使用翻译原理,而语义匹配打分函数使用合成运算符. 编码模型(尤其是神经网络)在建模实体和关系的交互过程中起着至关重要的作用. 双线性模型也引起了很多关注,一些张量分解模型也可以视为该类方法. 其他方法包含文本描述,关系/实体类型和实体图像的辅助信息.
传统的图表示方法直接基于其拓扑结构,存在稀疏性、高计算复杂性等问题.这促使了基于机器学习表示方法的出现,除了图的拓扑结构以外,此类方法还尝试捕获额外信息的潜在表示. 传统的网络嵌入方法很难再高度非线性结构中取得好的效果,深度学习在处理非线性结构中的成功促使对基于深度学习表示方法的大量尝试,本文对图形嵌入技术的回顾涵盖了四大类方法:( 1 ) 基于矩阵特征向量计算的方法,( 2 )基于随机游走的方法,( 3 )基于深度学习的方法以及( 4 )保存特殊性质的网络表示的方法.本文概括了图形嵌入技术以及每种方法类别所面临的挑战.本文报告了嵌入的各种应用及其各自的评估指标.通过调研,在图形嵌入领域中存在三个有前途的研究方向:(1)探索非线性模型;(2)研究网络的演化;(3)生成具有真实世界特征的合成网络.如调查所示,一般的非线性模型(例如基于深度学习的模型)在捕获图形的固有动态方面显示出了巨大的希望.它们具有近似任意函数的能力,该函数可以最好地解释网络边缘,并且这可以导致网络的高度压缩表示.这种方法的一个缺点是可解释性有限.专注于解释这些模型所学习的嵌入的进一步研究可能会非常有成果.
对基于翻译模型(Trans系列)的知识表示学习单独介绍(见3.5节),并介绍了图卷积网络在关系抽取的作用(见3.6节). 下面讨论知识图谱表示结合图嵌入应用的未来方向.
六、知识图谱表示结合图嵌入应用的未来方向
复杂推理:用于知识表示和推理的数值计算需要连续的向量空间来捕获实体和关系的语义. 尽管基于嵌入的方法在复杂的逻辑推理上有局限性,但值得进一步探讨关系路径和符号逻辑的两个方向. 诸如循环关系路径编码,基于 GNN 的消息在知识图上传递以及基于强化学习的路径查找和推理等一些有前途的方法对于处理复杂的推理非常有前途. 对于逻辑规则和嵌入的组合,最近的工作将 Markov 逻辑网络与KGE相结合,旨在利用逻辑规则并处理其不确定性. 通过有效嵌入来启用概率推理来捕获不确定性和领域知识将是一个值得注意的研究方向.
统一框架:一些知识图表示学习模型已经被证明是等效的,例如,Hayshi和Shimbo 证明 HolE 和 ComplEx 在数学上等价于具有一定约束的链接预测. ANALOGY提供了包括 DistMult,ComplEx 和 HolE 在内的几种代表性模型的统一视图. Wang 等探索了几个双线性模型之间的联系. Chandrahas等探索了加性和乘性 KRL 模型的几何理解. 大多数工作分别使用不同的模型来制定知识获取、知识图谱补全和关系提取. Han等把他们放在同一框架下,提出了一个共同学习框架,在知识图和文本之间共享信息时使用共注意力. 现有研究很少探索对知识表示和推理的统一理解. 然而,以类似于图网络统一框架的方式进行的统一研究,将有必要弥合研究差距.
可解释性:知识表示和注入的可解释性是知识获取和实际应用中的关键问题. 研究者已经为解释性作了初步努力. ITransF 使用稀疏向量进行知识迁移,并通过注意力可视化进行解释. CrossE 通过使用基于嵌入的路径搜索为链接预测生成解释,探索了知识图的解释方案. 但是,尽管最近的神经模型已经获得了令人印象深刻的性能,但它们在透明度和可解释性方面受到了限制. 一些方法通过合并逻辑规则来提高互操作性,从而将黑盒神经模型和符号推理结合在一起. 可解释性可以说服人们相信预测. 因此,进一步的工作应该进入可解释性并提高预测知识的可靠性.
可扩展性;在大规模知识图中,可扩展性至关重要. 在计算效率和模型表达能力之间需要权衡取舍,数量有限的工作可应用于一百万个以上的实体的知识图谱. 几种嵌入方法使用简化来降低计算成本,例如,使用循环相关运算简化张量积. 但是,这些方法仍然难以扩展到数百万个实体和关系. 诸如使用马尔可夫逻辑网络之类的概率逻辑推理需要大量计算,因此难以扩展到大规模知识图. 最近的神经逻辑模型[84]中的规则是通过简单的蛮力搜索生成的,从而使其在大规模知识图上不足. ExpressGNN 尝试使用NeuralLP 进行有效的规则归纳. 但是,要处理繁琐的深层架构和日益增长的知识图还有很长的路要走.
知识聚合:全局知识的聚集是知识感知应用程序的核心. 例如,推荐系统使用知识图对用户项目交互和文本分类进行建模,以共同将文本和知识图编码到语义空间中. 当前大多数知识聚合方法都设计神经结构,例如注意力机制和GNN. 通过 Transformer 和诸如BERT模型之类的变体进行的大规模预训练,促进了自然语言处理社区的发展,而最近的一项发现显示,在非结构化文本上进行预训练的语言模型实际上可以获取某些事实知识. 大规模的预训练可能是直接注入知识的方法. 但是,以有效和可解释的方式重新考虑知识聚合的方式也很重要.
自动构建与变化:当前的知识图高度依赖于人工构建,这是劳动密集型且昂贵的. 知识图在不同认知智能领域的广泛应用需要从大规模的非结构化内容中自动构建知识图. 最近的研究主要是在现有知识图的监督下进行半自动构建. 面对多模式,异构性和大规模应用,自动构建仍然是巨大的挑战. 主流研究集中在静态知识图上,在预测时间范围的有效性以及学习时间信息和实体动力学方面进行了一些工作. 许多事实仅在特定时间段内有效. 考虑到时间性,动态知识图可以解决传统知识表示和推理的局限性.
参考文献
[1] Smriti Bhagat, Graham Cormode, and S. Muthukrishnan. Node Classification in Social Networks, pages 115–148. Springer US, Boston, MA, 2011. ISBN 978-1-4419-8462-3. doi: 10.1007/978-1-4419-8462-3_5. URL https://doi. org/10.1007/978-1-4419-8462-3_5.
[2] S. V. N. Vishwanathan, Nicol N. Schraudolph, Risi Kondor, and Karsten M. Borgwardt. Graph Kernels. Journal of Machine Learning Research (JMLR), 11(Apr):1201–1242, April 2010. URL http://www.jmlr.org/papers/v11/ vishwanathan10a.html.
[3] David Liben-Nowell and Jon Kleinberg. The Link-Prediction Problem for Social Networks. Journal of The American Society for Information Sci- ence and Technology, 58(7):1019–1031, 2007. doi: 10.1002/asi.20591. URL https://onlinelibrary.wiley.com/doi/abs/10.1002/asi.20591.
[4] Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. DeepWalk: Online Learn- ing of Social Representations. In Proceedings of the 20th ACM SIGKDD In- ternational Conference on Knowledge Discovery and Data Mining, KDD ’14, pages 701–710, New York, NY, USA, 2014. ACM Press. ISBN 978-1-4503- 2956-9. doi: 10.1145/2623330.2623732. URLhttp://doi.acm.org/10.1145/ 2623330.2623732.
[5] Wayne W. Zachary. An Information Flow Model for Conflict and Fission in Small Groups. Journal of Anthropological Research, 33(4):452–473, 1977. doi: 10.1086/jar.33.4.3629752. URL https://doi.org/10.1086/jar.33.4. 3629752.
[6] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding. Science, 2000, 290: 2323–2326.
[7] Saul L K, Roweis S T. An introduction to locally linear embedding. 2000. http://www.cs.toronto.edu/roweis/lle/ publications.html.
[8] Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In: Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, 2001. 585–591.
[9] Tang L, Liu H. Leveraging social media networks for classification. Data Min Knowl Discov, 2011, 23: 447–478.
[10] Chen M, Yang Q, Tang X. Directed graph embedding. In: Proceedings of the 20th International Joint Conference on Artifical Intelligence, Hyderabad, 2007. 2707–2712.
[11] Tu C, Wang H, Zeng X, et al. Community-enhanced network representation learning for network analysis. arXiv:1611.06645.
[12] Thomas L G, Mark S. Finding scientific topics. Proc National Acad Sci, 2004, 101: 5228–5235.
[13] Y. J. Wang, G. Y. Wong, Stochastic blockmodels for directed graphs, Journal of the American Statistical Association 82 (397) (1987) 8–19.
[14] W. W. Zachary, An information flow model for conflict and fission in small groups, Journal of anthropological research 33 (4) (1977) 452– 473.
[15] L. Tang, H. Liu, Relational learning via latent social dimensions, in: Proceedings of the 15th international conference on Knowledge discovery and data mining, ACM, 2009, pp. 817–826.
[16] L. Tang, H. Liu, Scalable learning of collective behavior based on sparse social dimensions, in: Proceedings of the 18th ACM conference on Information and knowledge management, ACM, 2009, pp. 1107–1116.
[17] J. Gehrke, P. Ginsparg, J. Kleinberg, Overview of the 2003 kdd cup, ACM SIGKDD Explorations 5 (2).
[18] J. Leskovec, A. Krevl, SNAP Datasets: Stanford large network dataset collection, http://snap.stanford.edu/data (2014).
[19] William L. Hamilton, Rex Ying, and Jure Leskovec. Representation Learning on Graphs: Methods and Applications. Bulletin of The IEEE Computer Society Technical Committee on Data Engineering, 40(3):52–74, 2017. URL http: //sites.computer.org/debull/A17sept/p52.pdf.
[20] Ziwei Zhang, Peng Cui, and Wenwu Zhu. Deep Learning on Graphs: A Survey.
arXiv.org, December 2018. URL http://arxiv.org/abs/1812.04202v1.
[21] A. Ahmed, N. Shervashidze, S. Narayanamurthy, V. Josifovski, A. J. Smola, Distributed large-scale natural graph factorization, in: Proceedings of the 22nd international conference on World Wide Web, ACM, 2013, pp. 37–48.
[22] J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, Q. Mei, Line: Largescale information network embedding, in: Proceedings 24th International Conference on World Wide Web, 2015, pp. 1067–1077. [23] D. Wang, P. Cui, W. Zhu, Structural deep network embedding, in: Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining, ACM, 2016, pp. 1225–1234.
[24] M. Ou, P. Cui, J. Pei, Z. Zhang, W. Zhu, Asymmetric transitivity preserving graph embedding, in: Proc. of ACM SIGKDD, 2016, pp. 1105– 1114.
[25] M. Belkin, P. Niyogi, Laplacian eigenmaps and spectral techniques for embedding and clustering, in: NIPS, Vol. 14, 2001, pp. 585–591.
[26] S. T. Roweis, L. K. Saul, Nonlinear dimensionality reduction by locally linear embedding, Science 290 (5500) (2000) 2323–2326.
[27] S. Cao, W. Lu, Q. Xu, Grarep: Learning graph representations with global structural information, in: Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, ACM, 2015, pp. 891–900.
[28] B. Perozzi, R. Al-Rfou, S. Skiena, Deepwalk: Online learning of social representations, in: Proceedings 20th international conference on Knowledge discovery and data mining, 2014, pp. 701–710.
[29] A. Grover, J. Leskovec, node2vec: Scalable feature learning for networks, in: Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining, ACM, 2016, pp. 855–864.
[30] S. Cao, W. Lu, Q. Xu, Deep neural networks for learning graph representations, in: Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, AAAI Press, 2016, pp. 1145–1152.
[31] T. N. Kipf, M. Welling, Semi-supervised classification with graph convolutional networks, arXiv preprint arXiv:1609.02907.
[32] Ji S , Pan S , Cambria E , et al. A Survey on Knowledge Graphs: Representation, Acquisition and Applications[J]. 2020.