『深度学习模型实现与技术总结』——AlexNet

一、简介

AlexNet是由Alex Krizhevsky提出的卷积神经网络，它在ImageNet LSVRC-2010比赛中夺得冠军并且远超第二名，证明依靠深度学习得到的特征可以优于手工设计的特征，掀起了CNN的浪潮。它在深度学习的发展过程中具有里程碑意义。

二、特点

1.ReLU

• 饱和与非饱和函数：当x趋向于正无穷与负无穷时，函数的导数都趋近于0，此函数即为饱和函数如Sigmoid和tanh，否则为非饱和函数如ReLU。
• 非饱和函数优点：1.解决梯度消失。 2.加快收敛速度。

AlexNet使用非饱和函数ReLU作为激活函数，函数图像如下：

$$f(x)=max(0,x)$$

2.LRN与BN

归一化（Normalization）：将一列数据变化到某个固定区间，在神经网络中可以使网络更快收敛并且避免数值问题。

LRN（Local Response Normalization）：源自于生物学中的一个概念，叫做侧抑制(lateral inhibitio)，指的是被激活的神经元会抑制它周围的神经元。

LRN的作用是：对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。论文公式如下：
$$b_{x,y}^i=a_{x,y}^i(k+\alpha \sum _{j=max(0,i-n/2)}^{min(N-1,i+n/2)}(a_{x,y}^j{)}^2{)}^{\beta }$$
i表示第i个通道，n是自定义的邻近通道的个数(前n/2个，后n/2个)，N是通道的总数。k,α,β,n都是自定义的超参数，x,y表示在通道上的位置。可以理解为对应位置的输出值是根据指定的前后各n/2个位于相近通道的相同位置的值进行归一化得到的。

原论文提到LRN在Imagenet上获得了1.4%的提升，但在后来实验中有研究者发现LRN影响不大，却会大幅增加计算量，所以它的实际使用较少，大多都是直接使用BN（Batch Normalization）。

ICS（Internal Covariate Shift）：在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。

ICS主要会导致两个问题：

1. 上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低。
2. 网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度

为了解决上述问题，先是提出了白化（Whitening）：使得输入特征分布具有相同的均值与方差，并去除了特征之间的相关性。但白化存在计算成本高与信息丢失两个不足之处，于是又提出了BN。

BN（Batch Normalization）：针对每一批数据，在网络的每一层输入之前增加归一化处理。BN是针对通道进行规范化，并引入两个可学习参数λ与β以保有数据原有的表达能力，减少信息丢失。

BN的作用可以总结为以下几点：

1. 规范化数据分布，加快学习速度
2. 抑制整体向非线性函数的取值区间上下限靠近，可以避免梯度消失
3. 具有一定的正则化效果，可以防止过拟合

3.Dropout

Dropout是指在训练网络时，按照一定概率将神经元暂时丢弃，即其权重不参与计算与更新。这样每次的网络结构都存在一定的不确定性，那么对于单个神经元来说，它对整个网络的输出所产生的影响相对减弱，而丢弃了它所形成的新的网络结构被迫学习更加具有适应性的特征。而对于多个神经元来说，相互之间的联系由于被迫断开，它们的共同作用减弱，之间的依赖关系减少，但每个新的网络结构所具有的信息表达的学习能力都相对与之前的网络更大了。

对于其中抑制过拟合一方面也可以类比为，在训练一个团体的能力时，可能会存在几个具有较强能力的人，那么我们每次训练他们时随机选取一些人停止训练，而原本他们所承担的任务分配给了仍旧参与训练的人，那么参与训练的人能力被迫得到提升。多次如此，团体中的个体也就学习到了比原本特征更加鲁棒的特征，那么也就起到了抑制过拟合的作用。

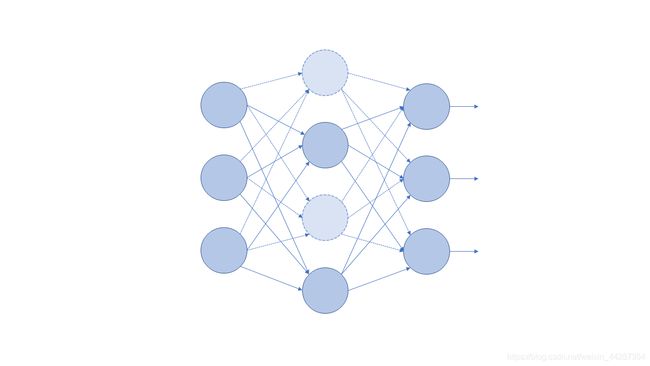
Dropout一般设置失活概率p=0.5，因为此时所有神经元的排列组合数取得最大。
下图虚线为丢弃的单元，在本轮训练中失活，不进行传播。

三、网络结构

1.224与227

• AlexNet中输入图片的尺寸是224*224还是227*227?

阅读多篇AlexNet的相关文章，可以发现在输入图片的尺寸上存在两种不同的看法，一种是224*224，一种是227*227。

阅读原论文可以看到，网络的输入图片的尺寸是224*224，但是使用11*11的卷积核，stride=4进行卷积后，所输出的feature map应该是54*54，但从结构图可以看到输出的尺寸是55*55。根据此输出尺寸反向计算可以得到输入为227*227，在很多其他的AlexNet实现也可以看到是采用的227*227，有的解释为是预处理之后变为了227*227，也有解释为原论文作者笔误。不过我个人认为这里应该是在第一层卷积时进行了padding=2，55=$\frac{224+2\ast 2-11}{4}+1$，这样的话也能顺利推导得出下一feature map的尺寸。

2.具体结构

1. 卷积：96个11*11卷积核，stride=4，padding=2；ReLU；maxpool(3*3,2)；BatchNorm
2. 卷积：256个5*5卷积核，stride=1，padding=2；ReLU；maxpool(3*3,2)；BatchNorm
3. 卷积：384个3*3卷积核，stride=1，padding=1；ReLU
4. 卷积：384个3*3卷积核，stride=1，padding=1；ReLU
5. 卷积：256个3*3卷积核，stride=1，padding=1；ReLU；maxpool(3*3,2)
6. FC：256*5*5->4096；ReLU；Dropout
7. FC：4096->4096；ReLU；Dropout
8. FC：4096->1000
   （使用了双GPU故结构图上分为上下两部分，代码注释为96=2*48，256=2*128，384=2*192）

四、代码实现

1.Pytorch

class AlexNet(nn.Module):
    def __init__(self, num_classes=1000):
        super(AlexNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(3, 96, 11, 4, 2),  # 3*224*224->2*48*55*55
            nn.ReLU(),
            nn.MaxPool2d(3, 2),  # 2*48*27*27
            nn.BatchNorm2d(96),
            nn.Conv2d(96, 256, 5, padding=2),  # 2*128*27*27
            nn.ReLU(),
            nn.MaxPool2d(3, 2),  # 2*128*13*13
            nn.BatchNorm2d(256),
            nn.Conv2d(256, 384, 3, padding=1),  # 2*192*13*13
            nn.ReLU(),
            nn.Conv2d(384, 384, 3, padding=1),  # 2*192*13*13
            nn.ReLU(),
            nn.Conv2d(384, 256, 3, padding=1),  # 2*128*13*13
            nn.MaxPool2d(3, 2),  # 2*128*6*6
            nn.Flatten()
        )
        self.fc = nn.Sequential(
            nn.Linear(256*6*6, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, num_classes),
        )

    def forward(self, input):
        output = self.conv(input)
        output = self.fc(output)
        return output

• 打印网络结构

net = AlexNet()
summary(net, (3, 224, 224))   # 查看网络结构

2.PaddlePaddle

import paddle
import paddle.nn as nn

class AlexNet(nn.Layer):
    def __init__(self, num_classes=1000):
        super(AlexNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2D(3, 96, 11, 4, 2),  # 3*224*224->2*48*55*55
            nn.ReLU(),
            nn.MaxPool2D(3, 2),  # 2*48*27*27
            nn.BatchNorm2D(96),
            nn.Conv2D(96, 256, 5, padding=2),  # 2*128*27*27
            nn.ReLU(),
            nn.MaxPool2D(3, 2),  # 2*128*13*13
            nn.BatchNorm2D(256),
            nn.Conv2D(256, 384, 3, padding=1),  # 2*192*13*13
            nn.ReLU(),
            nn.Conv2D(384, 384, 3, padding=1),  # 2*192*13*13
            nn.ReLU(),
            nn.Conv2D(384, 256, 3, padding=1),  # 2*128*13*13
            nn.MaxPool2D(3, 2),  # 2*128*6*6
            nn.Flatten()
        )
        self.fc = nn.Sequential(
            nn.Linear(256*6*6, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, num_classes),
        )

    def forward(self, input):
        output = self.conv(input)
        output = self.fc(output)
        return output

五、相关参考

1. 论文原文:“ImageNet Classification with Deep Convolutional Neural Networks”
2. “Batch Normalization原理与实战”
3. “深入理解Batch Normalization”
4. “理解dropout”
5. “深度学习饱受争议的局部响应归一化(LRN)详解”