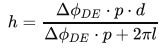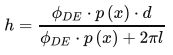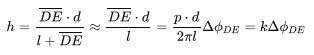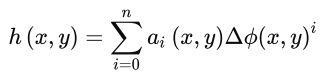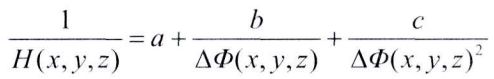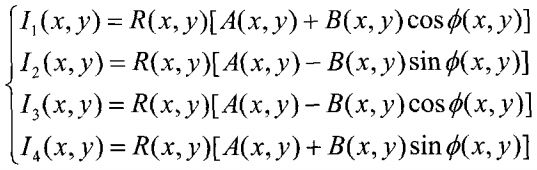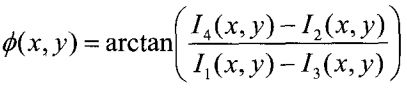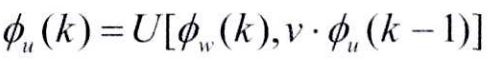三维重建之条纹投影结构光（一）

        该系列为条纹投影结构光学习笔记，一共分为四篇。第一篇记录文献阅读的笔记，对重要知识点进行摘录介绍；第二篇为相位求解和相位展开；第三篇为相高模型的标定；第四篇为重构篇。

        本篇以理论知识为主，主要从以下三个方面进行介绍，首先介绍条纹投影的三维重建测量原理；然后介绍相位和高度的模型，即相-高模型，最后介绍相位主值的求解和相位展开。本篇博文不涉及具体的代码实现。

---

条纹投影结构光测量原理

参考论文来源：结构光三维成像技术，四川大学，苏显渝

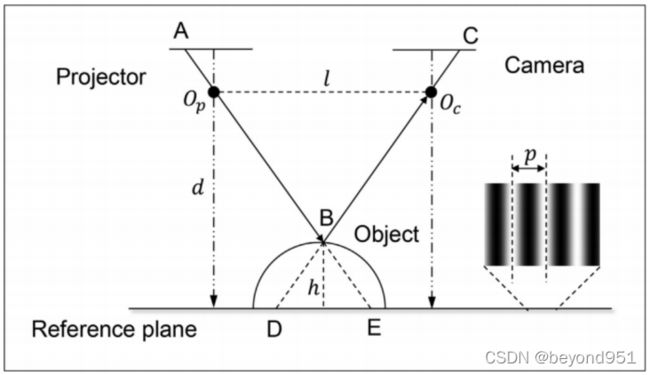
        结构光三维成像技术是一种利用辅助的结构光照明获取物体三维像的技术，它采用的技术方案是投影一个载频条纹到被成像的物体表面，利用成像设备从另一个角度记录受被成像物体高度调制的变形条纹图像，再从获取的变形条纹图中数字解调重建出被测物体的三维数字像。其成像系统示意图如下图所示：

        为什么相位可以反映物体的高度信息？

        当一个正弦光栅图形被投影到三维漫反射物体表面时，从成像系统获取的变形光栅像可表示为：

        式中Ｒ(ｘ,ｙ)是物体表面不均匀的反射率，即光学影像，包括物体表面的灰度和色度信息，C表示均匀的投影光强，相位函数Φ(ｘ,ｙ)表示了条纹的相位。当漫反射物体是一个标准平面（参考平面）时，条纹的相位具有线性分布的特点：

         式中Po为在参考平面上条纹的周期。当漫反射物体是分布在h(x,y)的三维表面时，增加了由高度引起的附加相位调制：

         式中λe为等效波长，一个等效波长正好等于引起2π相位变化量的高度变化。这时，从成像系统获取的变形光栅像可表示为

        由于物体表面的高度变化引起的条纹相位变化，导致观察到变形条纹。通过相移技术人们很容易从多帧相移条纹图形种分离出Φ(ｘ,ｙ)，从而重建h(x,y)的分布，通过相移技术也可以从条纹的调制度中分离 出Ｒ(ｘ,ｙ)，获 得 物 体 表 面 的 光 学 影 像。

        因此，市面上主流的投影重构方法基于Φ(ｘ,ｙ)求解出物体的真实高度信息；基于Ｒ(ｘ,ｙ)还原出物体的本身的色彩。

重要点：

        1、条纹投影实现物体的三维重建，是将相位-高度建立一个数学模型，得到相位之后可以得到物体的高度信息。

        2、我们知道相位是有取值范围的，为[0，2π]，但真实世界中物体的高度没有这种局限性，相位求出来是一个周期振荡的范围值。

        基于上面两个重点，引出后续两个重要概念：标定模型即相-高模型，相位值的求解和展开。

---

相位—高度模型

参考来源：Calibration of fringe projection profilometry: A comparative review，南京理工大学，左超

        标定模型一般可以分为两种，第一种为我们一直提到的相-高模型，即相位与真实世界高度的模型；第二种为三角立体模型，投影仪被当做逆相机（投影图案即当做投影仪成像图案），通过匹配相机、投影仪的相位同名点，利用三角测距法进行重建。第二种就是双目结构光，相位的作用用于标记每个图像上的像素点，然后相机1和相机2根据匹配到的点，利用三角测量进行重建。这部分内容在此不再赘述。下面对相高模型进行展开：

典型相位-高度模型

平行轴模型

        在早期相位高度模型中，投影仪和相机的光轴应该保持平行。两个轴都垂直于参考平面外，投 影仪和照相机距参考平面的距离相同。模型如图所示，其中： h是被测点B的高度、 d是从光学中心（Op和Oc）到参考平面的距离。

         根据三角测量原理，我们可以得到相高模型如下：

        其中：p,l,d是在相位-高度模型中我们需要进行标定的参数。只要系统固定，这些参数可以被手动地测 量。获得了相位差ΔΦDE，对于相机获取图片的每个像素点，我们都可以计算它的高度，结合它的坐标，即可获取三维几何形状。

        问题点：平行轴经典模型直观易懂，然而，几何约束在实际应用中难以满足、手工精确地测量参数也不容易、平行轴布置趋向于限制投影仪和照相机的共同视线，从而限制了测量大小、需要参考平面。

非平行轴模型

        非平行轴模型消除了光轴平行假设，保持距离不变，并稍微旋转相机或投影仪，如图所示。

         非平行轴模型第一种情况，因为投影仪并没有旋转，故平行轴模型适用。旋转投影仪，投射在参考平面上的条纹分布将不再均匀，相位高度模型变为：

        其中：投影条纹的宽度从常数p变为由参考平面上的位置确定的变量p(x) 。变化的条纹导致载波频率的非线性空间分布。为了解决这个问题，可以显式导出p(x)的分布或对投影的条纹图案进行预失真。

---

线性相位—高度模型

        在平行轴相位—高度模型基础上，如果l>>DE，则公式可以进一步简化

         可以得到如下模型：

        其中， k是唯一要标定的参数。为了提升精度，如果测量整个对象，最好按像素映射计算k （因为平面 不是绝对平面），公式如下：

         要计算像素参数k(x,y)，我们只需测量一次已知高度的参考平面在理论上。 但是，建议在不同的高度 进行更多的测量，以提高标定的k(x,y)的精度，这可以通过应用最小二乘算法来解决。

         线性模型的优点在于它简单易行，并且无需繁重的计算量即可进行计算。然而，当不满足假设l>>DE时，测量精度有限。

---

逆线性相位—高度模型

         为了解决严格的几何约束，研究人员开发了一种灵活的模型，其中对系统配置没有严格的几何约束 。由于相互之间的高度和相互之间的相位差之间存在线性关系，因此在本文中将其称为逆线性相高模型。在此模型中，摄像机和投影仪可以任意部署，只要它们可以照亮并捕获被测物体即可。

逆线性（1）

        相位-高度可以由如下关系表示：

         数学模型表达式为：

        其中，ΔΦ(x,y)是相位差，a(x,y)，b(x,y)是待标定参数。

逆线性（2）

        对于上述公式，进行移项可得：

         两个公式看似是一样的，事实上性能是有所不同的。由于测量噪声的存在，公式 重建的误差与物体高度相关，物体越高，误差越大。作为对比，公式 在同样环境下算法鲁棒性更高。

---

多项式相位—高度模型

        上述逆线性相位—高度模型也可以表示为：

         该方程式显示出高度 与相位差 之间的非线性关系。因此，可以使用非线性最小二 乘算法估计这些参数。但是，非线性拟合过程的性能取决于a(x,y)和b(x,y)的初始值，这可能会影响 算法的稳定性。为了解决这个问题，研究人员提出了一种多项式拟合方法来近似这种非线性关系， 令：

        其中：ai(x,y)是逐像素的系数需要去标定。系数通常在标定后保存，然后在3D测量期间加载。实际上，通过增加多项式的度数可以减轻相机、投影仪的透镜畸变对表面重构 的影响。但是，应谨慎调整 ，因为使用高级多项式函数时可能会发生Runge现象。

         后续相高模型的标定正是基于这一多项式的模型，但将h(x,y)的倒数与相位的倒数进行展开，其模型如下所示：

        基于这个模型可以看到，相高模型标定的过程为a、b、c三个参数求解的过程。这里参考的来源为：利用三频外差实现的小视场三维测量系统，四川大学，艾佳；后续相位的求解和展开也是基于这篇论文。

        至此，相高模型总结完毕。接下来，对相位求解和相位展开进行阐述。

---

相位计算

        相位计算主要分为两步，第一步为相位主值求取；第二步为相位展开。这里针对四步相移法和三频外差法进行阐述。

相位主值求取—四步相移法

        通过一帧变形条纹 图样是很难得到高精度的相位Φ(ｘ,ｙ)，需要采用相移算法来准确测定相位。对条纹 图进行相移的方法有很多 ，比较常用的是N帧满周期等间距相移法 。投影 的正弦条纹每隔一个光栅周期的1／N 移动一次 ，并产生相应的光强函数 ，In(x,y)，此时正弦条纹的相位对应移动2π/N。四步相移算法 ，每次的相移增量为 π/2，故可以得到相应的四幅变形条纹图，这里假设In(x,y)(n=1,2,3,4) 代表第n幅图像光强 ，则：

         由上面可以计算得到的相位函数Φ(ｘ,ｙ)为

         由于是通过反正切 函数计算相位信息，因此所得的相位值都是被截断在(-π,π]区间内的不连续相位。 为 了得到连续 的相位分布 ，需要进行相位展开。采用三频外差方法进行相位展开。

相位展开—三频外差法

        三频外差法是一种时间相位展开方法 ，它是在三频展开法的基础上改进而来。通过投射三种不同频率的条纹图到物体表面，拍摄得到一组受物体表面调制的条纹图序列 ，然后将每点的相位沿时间序列独立进行展开 ，可以从原理上避免误差的传播。

         投影三套条纹周期数t=s-√s,s,s+√s+1的条纹图，由四步相移得到三幅截断相位图。之后进行两次外差，可以看出，第一次外差得到数目为(√s,√ s+1)的条纹图，再进行一次外差得到条纹周期数为 1的条纹图，其中外差即对应像素点相位相减。

         首先定义展开运算符U[ Φ1,Φ2 ]如下：

         其中NINT(·)为四舍五入取整运算。

        然后外差得到的条纹周期数为1的相位分布等同于Φw(1)等同于已展开的相位Φu(1)，以它为起始相位逐级向上进行相位展开：

        其中v=√s表示不同外差级次的倍率，而k逐级去2、3。通过最小二乘法对展开相位进行拟合，计算得到的斜率表示为：

        再将斜率乘以最大投影条纹数，即可得到最终的展开相位ΔΦ。

        综上上述，总结完毕。

        接下文：

三维重建之条纹投影结构光（二）——四步相移+三频外差法https://blog.csdn.net/beyond951/article/details/123769596?spm=1001.2014.3001.5501