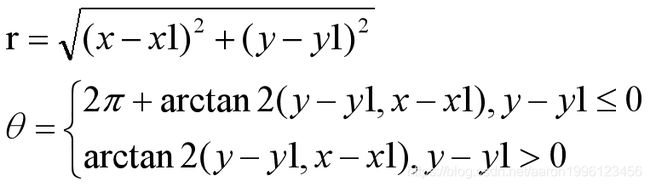读书笔记-opencv-极坐标变换
读书笔记-opencv-极坐标变换
原理解析
极坐标变换用来矫正图像中的圆形物体，或者包含在圆形物体中。
笛卡尔坐标系xoy平面上任意一点(x,y),以(x1,y1)为中心通过以下计算公式对应到极坐标系上的极坐标（θ，r）
极坐标变换后的角度范围[0, 360]
举例：（11, 13）以（3, 5）为中心进行极坐标变换
import math
r = math.sqrt(math.pow(11-3, 2) + math.pow(13-5, 2))
theta = math.atan2(13-5, 11-3)/math.pi*180 #转换为角度
print(r, theta)
opencv提供的函数：
x = np.array([[0,1,2],[0,1,2],[0,1,2]], dtype = "float64")-1
y = np.array([[0,0,0],[1,1,1],[2,2,2]], np.float64)-1
r, theta = cv2.cartToPolar(x,y, angleInDegrees = True)
print(r, theta)
angleInDegrees = True代表返回的是角度，反之返回的是弧度。array数据类型为浮点型，float32或者float64，x，y具有相同尺寸和数据类型的数组。
将极坐标转换为笛卡尔坐标系
已知极坐标（θ，r）的条件下，以笛卡尔坐标（x1，y1）为中心，
原坐标（x，y）可表示为：
x = x 1 + r c o s θ , y = y 1 + r s i n θ x = x_{1} + rcosθ, y = y_{1} + rsinθ x=x1+rcosθ,y=y1+rsinθ
opencv提供函数：
angle = np.array([[30,31], [30,31]], np.float32)
radiu = np.array([[10,10], [11, 11]], np.float32)
x, y = cv2.polarToCart(radiu, angle, angleInDegrees = True )
C++实现：
Mat angle = (Mat_(2,2) << 30, 31, 30, 31);
Mat radiu = (Mat_(2,2) << 10, 10, 11, 11);
Mat x, y;
polarToCart(radiu, angle, x, y, true);
函数参数和前面Python类似。
利用极坐标变换对图像进行变换
假设输入矩阵位I，（x1， y1）代表极坐标变换的中心，输出图像矩阵位O， 极坐标与笛卡尔坐标系一一对应的关系，即：
O ( I , θ ) = f I ( x 1 + r c o s θ , y 1 + r s i n θ ) O(I, θ) = f_{I}(x_{1} + rcosθ, y_{1} + rsinθ) O(I,θ)=fI(x1+rcosθ,y1+rsinθ)
这里的I， θ都是以1为步长，输出矩阵可能失真严重。进行改进，假设（x1， y1）的距离范围[rmin, rmax]，角度范围是[θmin, θmax]进行坐标和变换，进行离散化；假设r的变换步长为rstep，0
O ( i , j ) = f I ( x 1 + ( r m i n + r s t e p ∗ i ) ∗ c o s ( θ m i n + θ s t e p ∗ j ) , y 1 + ( r m i n + r s t e p ∗ i ) ∗ s i n ( θ m i n + θ s t e p ∗ j ) ) O(i,j) = f_{I}(x_{1} + (r_{min} + r_{step} * i)*cos(θ_{min} + θ_{step} *j), y_{1} + (r_{min} + r_{step} * i)*sin(θ_{min} + θ_{step} *j)) O(i,j)=fI(x1+(rmin+rstep∗i)∗cos(θmin+θstep∗j),y1+(rmin+rstep∗i)∗sin(θmin+θstep∗j))
代码实现：
import cv2
import numpy as np
import sys
import math
def polar(I, center, r, theta= (0,360), rstep = 1.0, thetastep = 360.0/(180*8)):
#得到距离最小最大的范围
minr, maxr = r
#得到角度最小最大范围
mintheta, maxtheta = theta
#
H = int((maxr - minr) / rstep) +1
W = int((maxtheta - mintheta) / thetastep) +1
O = 125 * np.ones((H, W), I.dtype)
#tile(a,(2,3))在垂直方向和水平方向上复制2，3次
#numpy.linspace(start, stop[, num=50[, endpoint=True[, retstep=False[, dtype=None]]]]])
#返回在指定范围内的均匀间隔的数字（组成的数组），也即返回一个等差数列
#start - 起始点，stop - 结束点，num - 元素个数，默认为50，
#endpoint - 是否包含stop数值，默认为True，包含stop值；若为False，则不包含stop值
#retstep - 返回值形式，默认为False，返回等差数列组，若为True，则返回结果(array([`samples`, `step`])),
#dtype - 返回结果的数据类型，默认无，若无，则参考输入数据类型。
#transpose用法详见https://blog.csdn.net/xiongchengluo1129/article/details/79017142
#极坐标变换
r = np.linspace(minr,maxr,H)
r = np.tile(r,(W,1))
r = np.transpose(r)
theta = np.linspace(mintheta,maxtheta,W)
theta = np.tile(theta,(H,1))
x,y=cv2.polarToCart(r,theta,angleInDegrees=True)
#最近邻插值
for i in range(H):
for j in range(W):
px = int(round(x[i][j])+cx)
py = int(round(y[i][j])+cy)
if((px >= 0 and px <= w-1) and (py >= 0 and py <= h-1)):
O[i][j] = I[py][px]
else:
O[i][j] = 125#灰色
return O
#主函数
if __name__ == "__main__":
imagePath = "G:\\blog\\OpenCV_picture\\chapter3\\img2.jpg" #"G:\\blog\\OpenCV算法精解-测试图片\\第3章\\image2.jpg"
image = cv2.imread(imagePath, cv2.IMREAD_GRAYSCALE)
#图像的宽高
h,w = image.shape[:2]
print (w,h)
#极左标变换的中心
cx,cy = 508,503
print (cx,cy)
cv2.circle(image,(int(cx),int(cy)),10,(255.0,0,0),3)
#距离的最小最大半径 #200 550 270,340
O = polar(image,(cx,cy),(0,550))
#旋转
O = cv2.flip(O,0)
#显示原图和输出图像
cv2.imshow("image",image)
cv2.imshow("O",O)
cv2.imwrite("O.jpg",O)
cv2.waitKey(0)
cv2.destroyAllWindows()
注意：xrange（）在opencv3里面合并到range（）
C++实现
先介绍repeat（）函数，重复函数与前面的tile（）函数类似。
void repeat(const Mat& sr, int ny, int nx)
src输入矩阵，ny将src在垂直方向上重复ny次， nx将src在水平方向上面重复nx次。
通过polar（）函数实现及坐标变换，参数I是输入图像，center十几座标变换中心，minr是与变换中心的最小距离，mintheta是最小角度，thetaStep是角度变换步长，rStep是距离变换步长，插值使用最邻近插值算法。
Mat polar(Mat I, Point2f center, Size size, float minr = 0, float mintheta = 0.0, float thetaStep = 1.0 / 4, float rStep = 1.0)
{
//构建半径矩阵
Mat r_i = Mat::zeros(Size(1, size.height), CV_32FC1);
for (int i = 0; i < size.height; i++)
{
r_i.at(i, 0) = minr + i * rStep;
}
Mat r = repeat(r_i, 1, size.width);
//构建角度矩阵
Mat theta_j = Mat::zeros(Size(size.width, 1), CV_32FC1);
for (int j = 0; j < size.height; j++)
{
theta_j.at(0, j) = mintheta + j * thetaStep;
}
Mat theta = repeat(theta_j, size.height, 1);
//将极坐标转化为笛卡尔坐标
Mat x, y;
polarToCart(r, theta, x, y, true);
//将坐标中心移到原点
x += center.x;
y += center.y;
//最邻近插值
Mat dst = 125 * Mat::ones(size, CV_8UC1);
for (int i = 0; i < size.height; i++)
{
for (int j = 0; j < size.width; j++)
{
float xij = x.at(i, j);
float yij = y.at(i, j);
int nearestx = int(round(xij));
int nearesty = int(round(yij));
if ((0 <= nearestx && nearestx < I.cols) && (0 <= nearesty && nearesty < I.rows))
{
dst.at(i, j) = I.at(nearestx, nearesty);
}
}
}
return dst;
}
int main()
{
std::string iamge_path = "G:\\blog\\OpenCV_picture\\chapter3\\img2.jpg";
Mat image = imread(iamge_path, 0);
if (!image.data)
{
return -1;
}
//图像极坐标变化
float thetaStep = 1.0 / 4;
float minr = 270;
Size size(int(360 / thetaStep), 70);
Mat dst = polar(image, Point2f(508, 503), size, minr);
//水平方向镜像处理
flip(dst, dst, 0);
//显示
imshow("I", image);
imshow("polar: ", dst);
waitKey(0);
return 0;
}
结果：
void filp(InputArray src, OutputArray dst, int flipCode)
flipCode : >0:src绕y轴镜像处理
：=0：src绕x轴镜像处理
： <0:src逆时针旋转180°，先绕x轴，再绕y轴镜像
flip（）函数进行的几何变换，不是通过仿射变换，而是行列互换，声明在core.hpp中。
线性极坐标函数linearPolar
void linearPolar(InutArray src, OutputArray dst, Point2f center, double maxRadius, int flags)
center:极坐标变换中心； maxRadius：极坐标变换的最大距离， flags：插值算法，与前文的resize() 和warpAffine()类似。
代码实现：
int main()
{
std::string iamge_path = "G:\\blog\\OpenCV_picture\\chapter3\\img2.jpg";
Mat image = imread(iamge_path, 0);
if (!image.data)
{
return -1;
}
Mat dst;
linearPolar(image, dst, Point2f(508, 503), 550, CV_INTER_CUBIC);
//这里采用的不是最邻近插值算法
imshow("InitImage", image);
imshow("PolarImage", dst);
waitKey(0);
return 0;
}
该函数存在两个缺点：极坐标变换的步长不可控，该函数只能对整个圆内区域进行变换，不可以对圆环进行操作。
void logPolar (InutArray src, OutputArray dst, Point2f center, double maxRadius, int flags)
该函数和linearPolar（）函数类似。