logistic回归分析优点_漫谈数据分析之建模算法

序

1、数据分析 & 建模

• 数据分析工作的核心是：发现和挖掘有用的信息，得出建设性的结论及辅助制定决策。其主要工作内容包括：数据获取、数据清洗、数据重构、数据建模、模型验证等。
• 众所周知，数据是分析的基础，数据的质量、数据的相关度、数据的维度等都会影响数据分析的结果。因此利用已经处理好的数据，建立模型，才是将数据的价值最大化发挥出来。
• 人工智能技术的兴起，机器学习和深度学习等算法模型在很多领域发挥中越来越重要的作用，如自动驾驶、人脸识别等领域。在数据分析工作中，这些优秀的算法模型也帮助我们更大地发现数据的价值，辅助业务决策。

2、建模关键

• 建模的主要流程：获取数据、清洗数据、训练模型，基于模型评估结果、数据特点或其他评价指标选择最好的模型。
• 工作中，我们基于模型类型采用均方误差（回归问题）、混淆矩阵、查准率、查全率、ROC曲线等进行模型验证；当然我们会选择错误率比较小的、准确率比较高的模型；其次，要在准确率和模型复杂度之间权衡；
• 有些领域，如金融领域，倾向于选择解释性好的算法模型；一般来说，模型越复杂就越难以解释。比如线性回归只考虑自变量与因变量之间的线性相关关系，模型简单(难以处理复杂的关系)，好解释；而神经网络模型，可以在多个层次进行抽象推断，可以处理因变量与自变量之间非常复杂的关系，并且达到非常高的精度，但是其解释性就很差。

3、常见数据分析场景建模参考

• 市场营销场景中建模参考
  • 购物车分析（关联分析）
  • 客户细分（聚类）
  • 流失预警（逻辑回归）

• 风险管理场景中建模参考
  • 客户信用风险评分（逻辑回归，决策树）
  • 客户欺诈风险评分（逻辑回归，决策树）

• 总之，建模是为了解决特定场景下的关键问题，而不是为了建模而建模；故此针对不同的业务场景选择合适的模型算法；这也就要求数据分析师要了解常用的建模算法，包括但不限于：回归、分类、聚类等。

一、线性回归

1、模型简介

• 线性回归（Linear Regression）是一种简单，易于实现的监督学习算法，用于解决回归问题。
• 如果 2 个或者多个变量之间存在线性关系，我们可以挖掘出变量之前的线性关系，建立一个有效的模型，来预测未来的变量结果。线性回归的模型形如：

• 线性回归模型不一定是一条直线，可以是直线(二维空间)、平面(三维空间).....

2、模型的优缺点

• 线性回归的优点：
  • 建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快。
  • 有很好的可解释性，可以从权重W直接看出每个特征对结果的影响程度（这使得它在物理学、经济学、商学等领域中占据了难以取代的地位）。

• 线性回归的缺点：不能很好地拟合非线性数据，需要先判断变量之间是否是线性关系。

3、模型使用

# 线性回归 预测Boston房价
#1.导入库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
from sklearn import metrics
​
#2.导入数据
boston = datasets.load_boston()
data_x = boston.data
data_y = boston.target
​
#3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.1)
​
#4.模型训练
linear_regression= linear_model.LinearRegression()
linear_regression.fit(x_train,y_train)
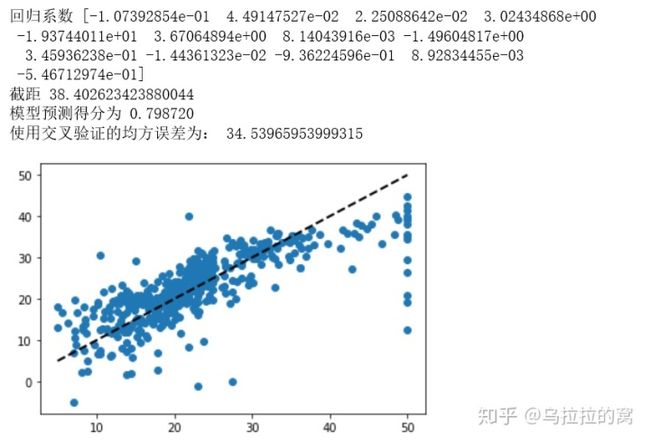
print("回归系数", linear_regression.coef_)
print("截距",linear_regression.intercept_)
​
#5.模型评估
print("模型预测得分为 %f" % linear_regression.score(x_test,y_test))
predicted = cross_val_predict(linear_regression,data_x,data_y,cv=10)
print("使用交叉验证的均方误差为：",metrics.mean_squared_error(data_y,predicted))
​
#6.模型效果可视化
plt.figure('线性回归模型效果')
plt.scatter(data_y,predicted)
plt.plot([data_y.min(),data_y.max()],[data_y.min(),data_y.max()],'k--',lw=2)
plt.show()
​

二、逻辑回归

1、模型简介

• 逻辑（Logistic) 回归是一种简单，易于实现的监督学习算法，可用于解决分类问题；
• Logistic 回归使用 logistic 函数估计概率，来衡量因变量（预测标签）与一个或多个自变量（特征）之间的关系。
• logistic 函数也称Sigmoid 函数，它是一个 S 形曲线，它可以将任意实数值映射到介于 0 和 1 之间的值(不包括0和1)
• 为了得到最佳参数，使得被正确分类的概率最大，一般采用梯度下降法作为优化算法。梯度下降法的基本思想是：求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。

2、模型的优缺点

• Logistic回归的优点：
• 容易实现，训练高效，准确率好。在工作中，可以将其作为模型性能的基准，用来衡量其他更复杂算法的性能。
• Logistic 回归的缺点
  • 因为它的决策边界是线性的，不能用它来解决非线性问题。
  • 对特征变量的数据质量要求高（对异常数值敏感，要求特征变量之间相关性低）。
  • 在多特征、多类别的数据环境下，容易出现过拟合的情况。

3、模型使用(解决多分类问题）

• Logistic回归常用来解决二分类问题，但也可以利用技巧，来解决多分类问题。(以digits手写数字分类为例)
  • digits手写数字分类使用手写体 0 到 9 的数字图像的 MNIST 数据集，算法需要预测，哪个图像对应哪个数字，这是个多分类问题，主要办法有两个:
    • 一对多（OVA）: 为每个数字训练一个二分类器，共10个分类器。当对某个图像进行分类时，只需看看这10个分类器的预测分数哪个最高即可。
    • 一对一（OVO)：为每一对数字训练一个二分类器，共45个分类器(（N*（N-1）/ 2 ），N=10)。这意味着要训练一个可以区分 0 和 1 的分类器，一个可以区分 0 和 2 的分类器...; 当对某个图像进行分类时，分别运行这 45 个分类器，并选择性能最好的分类器。这个策略与其他策略相比有一个很大的优势，就是你只需要在它要分类的两个类别的训练集上进行训练。
  • 在算法实现上，sklearn可以识别何时使用二分类器进行多分类任务，并自动使用 OVA 策略。(支持向量机分类器，自动运行 OVO 策略)。

# 逻辑回归 digits手写数字分类
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
​
# 2.导入数据
digits = datasets.load_digits()
data_x = digits.data
data_y = digits.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.3)
​
# 4.模型训练
logisticregression = linear_model.LogisticRegression()
logisticregression.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % logisticregression.score(x_train,y_train))

三、K最邻近算法

1、模型简介

• K最邻近算法（KNN）是一种简单、易于实现的监督机器学习算法，可用于解决分类和回归问题。
• KNN针对给定测试样本，基于某种距离度量（一般用欧几里德距离）找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息来进行预测。
• KNN关键三要素：
  • K值的选择：一般根据样本分布选择一个较小的值，然后通过交叉验证来选择一个比较合适的最终值。
  • 距离度量：一般使用欧几里德距离
  • 决策规则：做回归和分类的主要区别在于最后做预测时的决策方式不同。
    • 分类预测决策规则：一般采用多数表决法或者加权多数表决法
    • 回归预测决策规则：一般采用平均值法或者加权平均值法

2、模型优缺点

• KNN优点：简单易行，不用迭代逼近，算法复杂度低，可用于分类和回归。
• KNN的缺点：
  • 不适合大数据量的训练，随着数据量的增加变得非常慢（KNN算法每次均需要计算所有点之间的距离），不适合需要快速做出预测的业务需求。
  • 对样本分布敏感，正负样本分布不均衡时对预测有明显影响。

3、模型使用

#使用KNN预测鸢尾花类别
​
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import neighbors
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
​
# 2.导入数据
liris = datasets.load_iris()
data_x = liris.data
data_y = liris.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.1)
​
# 4.模型训练
KNeighborsClassifier = neighbors.KNeighborsClassifier()
KNeighborsClassifier.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % KNeighborsClassifier.score(x_train,y_train))
​

四、朴素贝叶斯

1、模型简介

• 贝叶斯分类是以贝叶斯定理为基础的分类算法总称；其中，朴素贝叶斯是这类分类算法中最简单的一种（朴素贝叶斯是监督学习算法）。
• 朴素贝叶斯对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。（通俗理解：在街上看到一个黑人，十有八九猜非洲。其理由是：黑人中非洲人的比率最高，在没有其它可用信息下，我们会选择条件概率最大的类别）
• 贝叶斯定理公式如下：

• 我们经常可以很容易得出P(A|B)，很难直接得到P(B|A)，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路

2、模型优缺点

• 朴素贝叶斯优点：
  • 健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性。
  • 对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类。

• 朴素贝叶斯缺点：
  • 对数据样本的特征维度作了“彼此独立”的假设，在属性个数比较多或者属性之间相关性较大时，分类效果不好。
  • 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
  • 由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

3、模型使用

# 朴素贝叶斯 
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import naive_bayes
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
​
# 2.导入数据
liris = datasets.load_iris()
data_x = liris.data
data_y = liris.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.1)
​
# 4.模型训练
naive_bayes = naive_bayes.MultinomialNB()
naive_bayes.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % naive_bayes.score(x_train,y_train))
​
# 6.模型效果可视化
print(naive_bayes.predict(x_test))
print('------------------------------')
print(y_test)
​
​

在sklearn中实现了三类朴素贝叶斯：GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)

五、决策树（Decision Tree）

1、模型简介

• 决策树是一种逻辑简单、易于实现的，可解释性强，完全符合人类的直观思维的监督机器学习算法；可以用于解决回归和分类问题。
• 决策树算法采用树形结构，使用层层推理来实现最终的分类。决策树由下面几种元素构成：
  • 根节点：包含样本的全集
  • 内部节点：对应特征属性测试
  • 叶节点：代表决策的结果

• 决策树在预测时，在树的内部节点处用某一属性值进行判断，根据判断结果决定进入哪个分支节点，直到到达叶节点处，得到分类结果。(决策树的这些规则通过训练得到，而不是人工制定的)。
• 决策树学习的 3 个步骤:
  • 特征选择：筛选出跟分类结果相关性较高的特征，也就是分类能力较强的特征。通常使用的准则是：信息增益（ID3 算法）、信息增益比（C4.5 算法）、基尼系数（CART）。
  • 决策树生成：从根节点出发，对节点计算所有特征的信息增益，选择信息增益最大的特征作为节点特征，根据该特征的不同取值建立子节点；对每个子节点使用相同的方式生成新的子节点，直到信息增益很小或者没有特征可以选择为止（此为ID3 算法）。
  • 决策树剪枝：主要目的是对抗“过拟合”，通过主动去掉部分分支来降低过拟合的风险。

• 3种典型的决策树算法
  • ID3 算法：最早提出的决策树算法，他就是利用信息增益来选择特征的。
  • C4.5 算法： ID3 的改进版，引入“信息增益比”指标作为特征的选择依据。
  • CART（Classification and Regression Tree）：使用了基尼系数取代了信息熵模型，可以用于分类，也可以用于回归问题。

2、模型优缺点

• 决策树的优点：
  • 易于理解和解释，可以可视化分析，容易提取出规则。
  • 可以同时处理标称型和数值型数据；比较适合处理有缺失属性的样本。
  • 测试数据集时，运行速度比较快；在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

• 决策树的缺点：
  • 容易发生过拟合（随机森林可以很大程度上减少过拟合）；
  • 默认特征维度之间彼此独立，如果特征维度时间存在关联性，可能对预测结果产生影响；
  • 对于那些各类别样本数量不一致的数据，在决策树中，进行属性划分时，不同的判定准则会带来不同的属性选择倾向；信息增益准则对可取数目较多的属性有所偏好（典型代表ID3算法），而增益率准则（CART）则对可取数目较少的属性有所偏好，但CART进行属性划分时候不再简单地直接利用增益率尽心划分，而是采用一种启发式规则）（只要是使用了信息增益，都有这个缺点，如RF）。
  • ID3算法计算信息增益时结果偏向数值比较多的特征。

3、模型使用

# 决策树 预测 鸢尾花类别
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import sys
import pydotplus 
from sklearn import datasets
from sklearn import tree
from sklearn.model_selection import train_test_split
from IPython.display import Image
os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'
​
#2.导入数据集
iris = datasets.load_iris()
data_x = iris.data
data_y = iris.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.3)
​
#4.模型训练
decesiontree = tree.DecisionTreeClassifier()
decesiontree.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % decesiontree.score(x_train,y_train))
​
# 6.模型可视化
with open("iris.dot", 'w') as f:
    f = tree.export_graphviz(decesiontree, out_file=f)
dot_data = tree.export_graphviz(decesiontree, out_file=None, 
                         feature_names=iris.feature_names,  
                         class_names=iris.target_names,  
                         filled=True, rounded=True,  
                         special_characters=True)  
graph = pydotplus.graph_from_dot_data(dot_data)  
Image(graph.create_png()) 

六、随机森林

1、模型简介

• 随机森林(Random Forest)是一种由决策树构成的集成算法，可用于解决分类问题。
• 构造随机森林的 4 个步骤:
  • 假如有N个样本，则有放回的随机选择N个样本(每次随机选择一个样本，然后返回继续选择)。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
  • 当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
  • 决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
  • 按照以上三步建立大量的决策树，这样就构成了随机森林了。

• 随机森林预测分类的结果，由决策树的分类结果中最多的决定。

2、模型的优缺点

• 随机森林的优点：
  • 实现起来比较简单，训练速度比较快，容易做成并行方法。
  • 可以判断特征的重要程度，可以判断出不同特征之间的相互影响。
  • 对高维度（特征很多）的数据，不用降维，无需做特征选择。

• 随机森林的缺点：
  • 随机森林是一个“黑盒”，由随机生成的决策树组成，不存在明确的预测规则，解释性差。
  • 已经被证明在某些噪音较大的分类或回归问题上会过拟合。
  • 对于有不同取值的属性的数据，取值划分较多的属性会对随机森林产生更大的影响，所以随机森林在这种数据上产出的属性权值是不可信的。

3、模型使用

# 以预测鸢尾花类别 
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import ensemble
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
​
# 2.导入数据
liris = datasets.load_iris()
data_x = liris.data
data_y = liris.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.1)
​
# 4.模型训练
RandomForestClassifier = ensemble.RandomForestClassifier()
RandomForestClassifier.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % RandomForestClassifier.score(x_train,y_train))
​
# 6.模型效果可视化
print(RandomForestClassifier.predict(x_test))
print('------------------------------')
print(y_test)

七、支持向量机

1、简介

• 支持向量机（Support Vector Machine，SVM）是当最流行和最受关注的机器学习算法之一，用于解决分类问题。
• 向量其实就是样本点，每个样本都是一行数据；支持向量机是求解能够正确划分训练数据集并且几何间隔最大的分离超平面，这个平面上样本点就是支持向量。

2、特点

• 支持向量机的优点
  • 可以解决高维问题，即大型特征空间；能够处理非线性特征的相互作用。
  • 对异常值有较好的容忍度；计算速度快；具备高维空间操纵数据的能力。
  • 泛化能力比较强。

• 支持向量机的缺点
  • 当观测样本很多时，效率并不是很高。
  • 对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数。
  • 对缺失数据敏感。

3、模型使用

# 以预测鸢尾花类别 
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
​
# 2.导入数据
liris = datasets.load_iris()
data_x = liris.data
data_y = liris.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.1)
​
# 4.模型训练
svm = svm.SVC()
svm.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % svm.score(x_train,y_train))
​
# 6.模型效果可视化
print(svm.predict(x_test))
print('------------------------------')
print(y_test)
​
​

八、神经网络

1、模型简介

• 神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。
• 每个节点代表一种特定的输出函数，称为激励函数（activation function）。
• 每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。

2、模型特点

• 神经网络优点
  • 运算速度快，网络结果拓展性好；很很强的适应性、容错能力；

• 神经网络缺点
  • 神经网络是“黑盒算法”，可解释性差，往往依靠经验进行调参。

3、模型使用

# 以预测鸢尾花类别为例
​
# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import neural_network
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
​
# 2.导入数据
liris = datasets.load_iris()
data_x = liris.data
data_y = liris.target
​
# 3.划分训练集与测试集
x_train,x_test,y_train,y_test = train_test_split(data_x,data_y,test_size = 0.1)
​
# 4.模型训练 （MLPClassifier是多层感知器分类器）
neural_network = neural_network.MLPClassifier()
neural_network.fit(x_train,y_train)
​
# 5.模型评估
print("模型预测得分为 %f" % neural_network.score(x_train,y_train))

总结

• 本文简单介绍了，数据分析工作中最常见的机器学习算法模型。在实际工作中，需要针对具体的业务问题，结合不同模型的性能，可解释性等，选择真正合适的模型。
• 数据分析中的建模是为了解决实际问题，挖掘数据价值存在的，不是为了建模而建模；只有深入理解业务，结合业务特点，分析师才能利用好模型算法，为业务创建更大的价值。

本文引用到的参考资料如下：

• 线性回归 – linear regression
• 从原理到应用：简述Logistics回归算法
• Logistic Regression（逻辑回归）原理及公式推导
• 一文搞懂K近邻算法(KNN)，附带多个实现案例
• 朴素贝叶斯算法原理小结
• 决策树 – Decision tree
• 干货|简单理解神经网络几个基础问题