吴恩达机器学习课程-第一周
1.监督学习
数据集中的每个样本都有相应的“正确答案”,再根据这些样本作出预测
2.无监督学习
数据集中没有任何的标签/有相同的标签,将数据分为不同的簇
3.单变量线性回归
3.1 模型表示
只含有一个特征/输入变量: h θ ( x ) = θ 0 + θ 1 ( x ) h_\theta(x)=\theta_0+\theta_1(x) hθ(x)=θ0+θ1(x)
3.2 代价函数
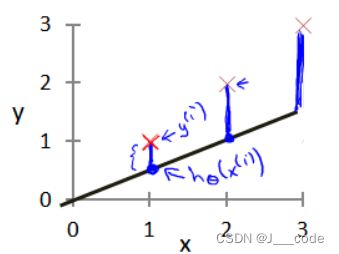
选择的参数决定了直线相对于训练集的准确程度,模型所预测的值与训练集中实际值之间的差距(下图中蓝线所指)是建模误差
目标便是选择出可以使得建模误差的平方和能够最小的模型参数,即使得下面代价函数最小:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
3.2.1 直观理解
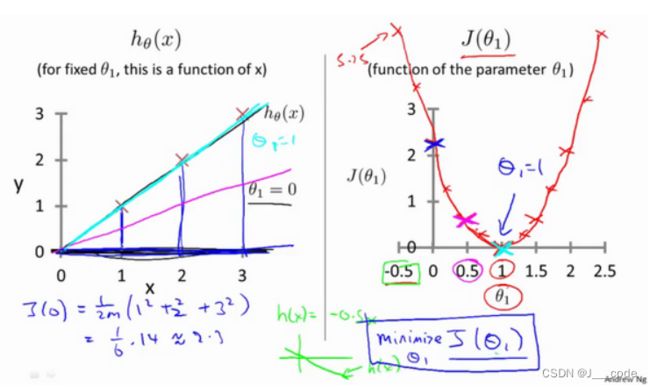
将 θ 0 \theta_0 θ0置为0的情况:
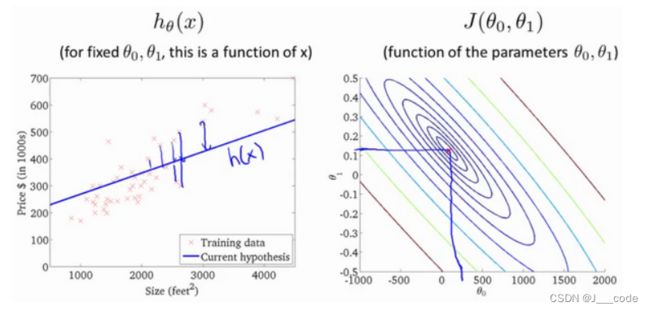
不将 θ 0 \theta_0 θ0置为0的情况:右图是代价函数的等高线图
3.3 梯度下降
在3.2中是通过人工的方式去观察代价函数值最小时,参数对应的值。当参数越来越复杂时肯定通过观察得到结果,所以使用梯度下降
3.3.1 思想
- 开始时随机选择一个参数的组合,计算代价函数,
- 寻找下一个能让代价函数值下降最多的参数组合
- 持续这么做直到到到一个局部最小值(选择不同的初始参数组合,可能会找到不同的局部最小值)
3.3.2 批量梯度下降
批量:在梯度下降的每一步中,用到了所有的训练样本(即计算的所有训练样本构成的 J ( θ ) J(\theta) J(θ)值)
重复执行下面公式直至收敛:需要同时更新 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1
θ j : = θ j − α d d θ J ( θ 0 , θ 1 ) \theta_j:=\theta_j-\alpha\frac{d}{d_{\theta}}J(\theta_0,\theta_1) θj:=θj−αdθdJ(θ0,θ1)
3.3.3 直观理解
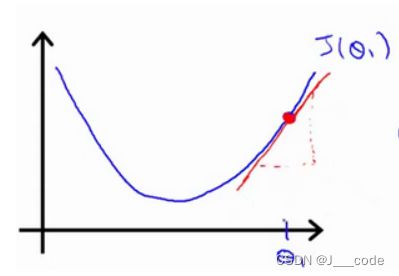
在红色点处,梯度 d d θ J ( θ 0 , θ 1 ) \frac{d}{d_{\theta}}J(\theta_0,\theta_1) dθdJ(θ0,θ1)方向是朝左下角(即为正数),所以 θ 1 \theta_1 θ1在不断减小, J ( θ ) J(\theta) J(θ)的值也在不断减小
为什么 α \alpha α可以不用改变也能收敛到局部最低点?因为当红色点在不断移动时,梯度大小也在不断减小
3.4 线性回归的梯度下降
对之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即:
d d θ j J ( θ 0 , θ 1 ) = d d θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{d}{d_{\theta_j}}J(\theta_0, \theta_1)=\frac{d}{d_{\theta_j}}\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 dθjdJ(θ0,θ1)=dθjd2m1∑i=1m(hθ(x(i))−y(i))2
j = 0 , d d θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) j=0,\frac{d}{d_{\theta_0}}J(\theta_0, \theta_1)=\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)}) j=0,dθ0dJ(θ0,θ1)=m1∑i=1m(hθ(x(i))−y(i))
j = 1 , d d θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) j=1,\frac{d}{d_{\theta_1}}J(\theta_0, \theta_1)=\frac{1}{m}\sum_{i=1}^m((h_\theta(x^{(i)})-y^{(i))}·x^{(i)}) j=1,dθ1dJ(θ0,θ1)=m1∑i=1m((hθ(x(i))−y(i))⋅x(i))
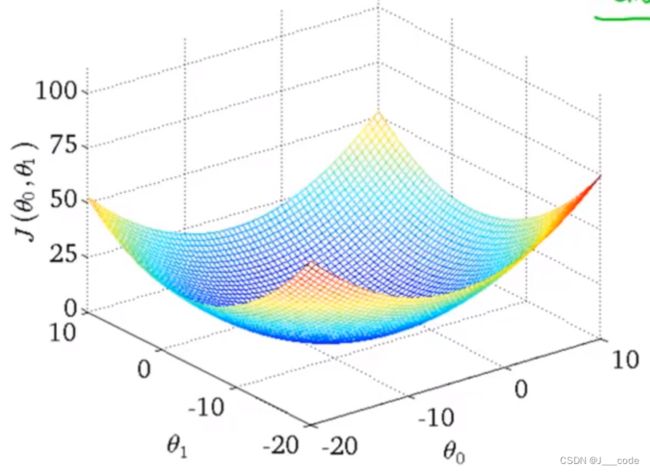
线性回归的 J ( θ ) J(\theta) J(θ)图像是一个凸函数图像,这种图像没有局部最优点,只有全局最优点:
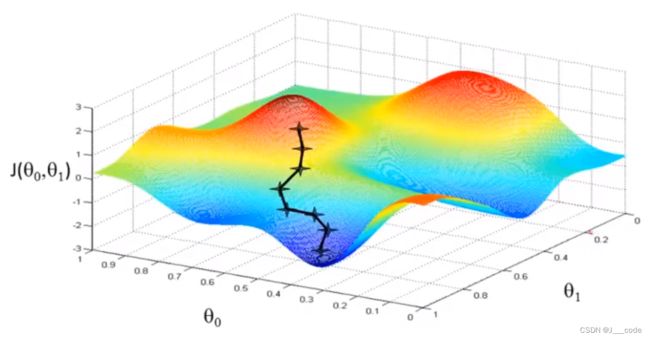
下面图像不是凸函数图像,会陷入到局部最优点上:
4.参考
https://www.bilibili.com/video/BV164411b7dx?p=3-11
http://www.ai-start.com/ml2014/html/week1.html