matlab使用遗传算法解决旅行商tsp问题
编码目的和解析
- 旅行商问题:
- 地图上有n个点,旅行商要求从一个点出发,经过每个城市一次且仅一次并最终回到出发城市,求最短路径
- 使用matlab作为编程工具,采用遗传算法对tsp(旅行商)问题进行基本编码实现和优化解答,最终控制误差在一定范围内,或者找到旅行商问题的最优解。
注:旅行商问题的已知最优解是通过遍历得到的,不可能通过智能算法得到更短的距离,除非计算公式出错或者数据出现问题。
数据获取
所需工具/软件/数据
软件:matlab
日志:csdn博客
资料来源:百度搜索的结果页面链接
搜索到的资料及其网址
-
《TSP的已知最优解》:百度文库网址 该文档的上传日期为2014年,该文档最后一行显示的时间点为2007年。
-
oschina中的数据集下载网址:MP-TESTDATA - The TSPLIB Symmetric Traveling Salesman Problem Instances
数据集和代码已经上传到csdn中,欢迎学习和交流
-
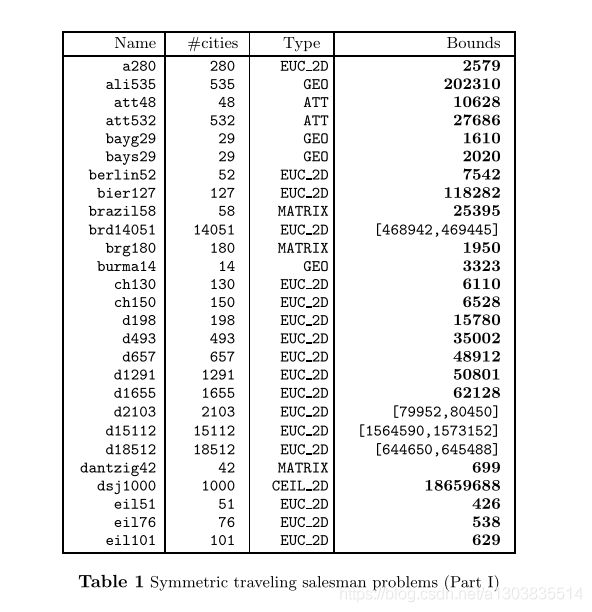
遇到的第一个问题是距离的计算问题,具体可以通过下载这个文件去查看具体数据集的距离计算公式:http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp95.pdf
文件第九页有每种问题的对应距离计算方法,再通过该方法找到具体的措施即可
举个例子:
a280数据集(图片中的第一个),可以找到Type为EUC_2D,在pdf文件中搜索该类型,即可找到对应的计算公式如下:
原理解析
种群确定与基本操作
- 首先要确定每个个体的元素和一个规模合适的种群
- tsp问题每个个体其实可以看做n个城市的链条
- 比如n = 5,<1,2,3,4,5>的排列顺序可以看成一个个体
- 1 2 3 4 5就是一个一个基因片段,后续重组变异也是基于此实现
- 确定种群的规模
- 和个体的基因数有关,一般规模不大时设置为100-1000即可
- 注意:规模越大,可能导致运算时间过长
- 到这里,对应实现种群的初始化即可
- 比如一千个个体,每个个体48个基因(n=48)随机排列
选择
- 是挑选父代的个体作为随后重组、变异的来源
- 主要有两种方法:轮盘赌和锦标赛(试验效果更好)
- 生成一个个体所需的父代一般是两个
- 所以使用两次算法得出两个个体参与重组、变异即可
轮盘赌:
- 结合tsp算法进行解释:
- 适应度:粗略理解为该个体生存下去的可能性的大小
- 在tsp问题中,可以理解为距离越小,适应度越高
- 所以可以取距离的倒数
- 求出父代每个个体的适应度,并进行累加得到max
- 这里需要生成一个数组,存放自第一个到第m个个体的累积适应度
- 例如有三个个体,适应度为0.2,0.5,0.7
- 生成的数组就是[0.2,0.7,1.4]
- 这里需要生成一个数组,存放自第一个到第m个个体的累积适应度
- 随后获得一个随机数 ran 在0-max之间
- 看看这个ran小于哪个累计数(0.2,0.7,1.4)就选择哪个个体
- 例如ran=0.6,则选择第二个个体,因为0.6>0.2且0.6<0.7
锦标赛
- 选择m个个体,选择适应度最高的个体作为父代
- 这个很简单,理解为在n个个体中选择m个个体,再比较这m个个体,选择距离最短的那个个体就行
- 例如种群数量有10个,随机选择5个个体(n=10,m=5)
- 这五个个体距离为:100,200,300,400,500
- 选择第一个个体,因为距离最小
重组
- 通过筛选出来的两个个体,即可进行重组运算
- 生物学上:重组就是选择父代两个相同位置的片段,交换上面的基因,形成新的个体
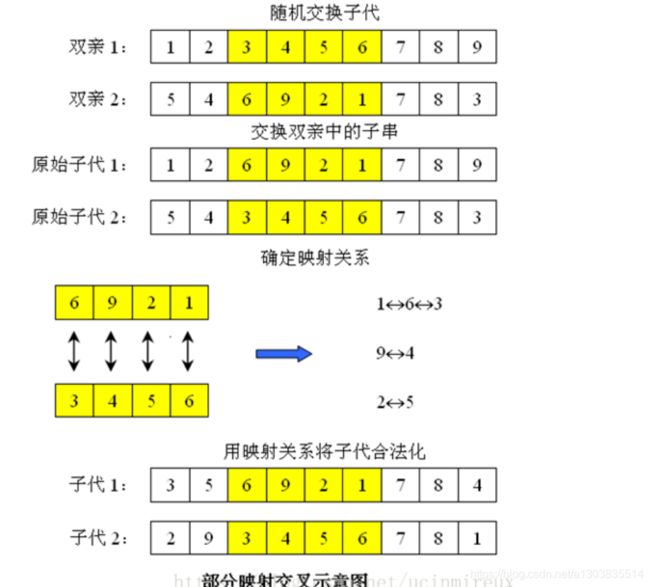
- 在tsp问题中,也是一样的,但是要考虑到如果交换了,可能出现某些城市出现了两次的情况
- 所以交换的时候采用以下的方法进行交换,看图解:
变异
- 随机选择两个基因进行交换即可
- 例如上图子代1的1和8交换,就变成了
- 3 5 6 9 2 8 7 1 4
- 变异的概率要控制好
- 太高的话,容易无法收敛到局部最优解
- 太低的话,收敛后无法跳出
代码解析
看不懂没关系,后面《最终代码》有更详细的代码,或者下载页面末尾的代码连接,下载到自己的电脑上,运行一下,看一下代码逻辑就懂了
页面读取逻辑
首先是一个初始化的参数设置
clear;
clc; %清空其他程序残留的变量
tStart = tic; % 算法计时器
%%%%%%%%%%%%自定义参数%%%%%%%%%%%%%
[cityNum,cities] = Read('att48.tsp');%读取tsp文件中的数据
cities = cities';%读取数据后进行反转
%cityNum = 100;
maxGEN = 1000;%设置迭代的次数
popSize = 1000; % 遗传算法种群大小
crossoverProbabilty = 0.9; %交叉概率
mutationProbabilty = 0.3; %变异概率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%存储最好的生成结果为最大值
gbest = Inf;
% 计算上述生成的城市距离
distances = calculateDistance(cities);
距离计算公式 --> 不同type不同
function [ distances ] = calculateDistance( city )
%计算距离
[~, col] = size(city);
distances = zeros(col);
for i=1:col
for j=1:col
distances(i,j)= sqrt( ((city(1,i)-city(1,j))^2 + (city(2,i)-city(2,j))^2) / 10);
end
end
end
Read方法–> 读取tsp文件
function [n_citys,city_position] = Read(filename)
fid = fopen(filename,'rt');
location=[];
A = [1 2];
tline = fgetl(fid);
while ischar(tline)
if(strcmp(tline,'NODE_COORD_SECTION'))
while ~isempty(A)
A=fscanf(fid,'%f',[3,1]);
if isempty(A)
break;
end
location=[location;A(2:3)'];
end
end
tline = fgetl(fid);
if strcmp(tline,'EOF')
break;
end
end
[m,n]=size(location);
n_citys = m;
city_position=location;
fclose(fid);
end
种群初始化
randperm(int[]) 将一列序号随机打乱,序号必须是整数。
find(square,1, ‘first’); 找出square中第一个非零元素
find(条件, -, -) 返回满足某条件的值
find(sumDistance==parent1,1, ‘first’);
选择方式
tourPopDistances=zeros( tournamentSize,1);
%选择了4个父代元素的距离
for i=1:tournamentSize
randomRow = randi(popSize);
tourPopDistances(i,1) = sumDistance(randomRow,1);
end
% 选择最好的,即距离最小的
parent1 = min(tourPopDistances);
% 选择第一个和距离最小的值匹配的个体
% 每个非零元素的行和列下标
[parent1X,parent1Y] = find(sumDistance==parent1,1, 'first');
parent1Path = pop(parent1X(1,1),:);
随机选择四个,选择里面最好的适应度的元素
然后找到对应的路径进行取出
锦标赛算法
每一代的更新方法
保留上一代最好的值,然后使用锦标赛算法
for gen=1:maxGEN
% 计算适应度的值,即路径总距离
% fval(n*1):适应度的值 sumDistance(n*1):总长度
% minPath(n*1):最小路径 maxPath(n*1):最大路径
[fval, sumDistance, minPath, maxPath] = fitness(distances, pop);
% 保留上一代的最好结果
[parent1X,parent1Y] = find(sumDistance==minPath,1, 'first');
offspring(1,:) = pop(parent1X(1,1),:);
minPathes(gen,1) = minPath;
fprintf('代数:%d 最短路径:%.2fKM \n', gen,minPath);
% 锦标赛选择
tournamentSize=20; %设置大小
for k=2:popSize
% 选择父代进行交叉 4*1
tourPopDistances=zeros( tournamentSize,1);
%选择了4个父代元素的距离
for i=1:tournamentSize
randomRow = randi(popSize);
tourPopDistances(i,1) = sumDistance(randomRow,1);
end
% 选择最好的,即距离最小的
parent1 = min(tourPopDistances);
% 选择第一个和距离最小的值匹配的个体
% 每个非零元素的行和列下标
[parent1X,parent1Y] = find(sumDistance==parent1,1, 'first');
parent1Path = pop(parent1X(1,1),:);
for i=1:tournamentSize
randomRow = randi(popSize);
tourPopDistances(i,1) = sumDistance(randomRow,1);
end
parent2 = min(tourPopDistances);
[parent2X,parent2Y] = find(sumDistance==parent2,1, 'first');
parent2Path = pop(parent2X(1,1),:);
subPath = crossover(parent1Path, parent2Path, crossoverProbabilty);%交叉
subPath = mutate(subPath, mutationProbabilty);%变异
offspring(k,:) = subPath(1,:);
end
% 更新
pop = offspring;
% 画出当前状态下的最短路径
if minPath < gbest
gbest = minPath;
paint(cities, pop, gbest, sumDistance,gen);
end
end
function [ fitnessvar, sumDistances,minPath, maxPath ] = fitness( distances, pop )
% 计算整个种群的适应度值
[popSize, col] = size(pop);
sumDistances = zeros(popSize,1);
fitnessvar = zeros(popSize,1);
for i=1:popSize
for j=1:col-1
sumDistances(i) = sumDistances(i) + distances(pop(i,j),pop(i,j+1));
end
end
minPath = min(sumDistances);
maxPath = max(sumDistances);
for i=1:length(sumDistances)
fitnessvar(i,1)=(maxPath - sumDistances(i,1)+0.000001) / (maxPath-minPath+0.00000001);
end
end
看不懂没关系,后面有改进方案,学后面的
最终代码
优化点:
-
在开头计算好所有城市的距离矩阵(n*n),在之后的适应度计算中,直接读取矩阵中的数据即可,大大减轻计算压力
-
直接选择父代最好的一半元素作为下一代的父代,并从中随机选择两个进行交叉变异获得新个体
-
保留每一代最好的个体
-
初始化种群的时候不要随意初始化,使用贪婪算法进行初始化–> 对大数据集优化明显
- 任选一个城市作为初始节点
- 选择距离这个城市最短距离的城市作为下一个节点
- 随后跳转到【下一个节点】,并重复执行上一步操作,知道找到一条"贪婪算法最短链"
- 注意:找的时候已经找过的点不要再用了,可以使用一个zeros(n)数组保存是否已经被使用,使用过了就置为1,没有就还是0,读取对应位置的元素进行替换即可,非常快速
-
变异的时候变异多个基因
- 效果不大
-
重组的时候重组多个部分
- 效果好一点
-
设置超过200次,变异概率提高
- 效果好点
-
设置超过1000次,跳出循环
- 为了避免长时间无效运转
实验成果举例
迭代收敛图
路线图
tsp主程序代码
clear;
clc;
tStart = tic; % 算法计时器
%%%%%%%%%%%%自定义参数%%%%%%%%%%%%%
[ctype,cityNum,cities] = Read('att48.tsp');
cities = cities';
%cityNum = 100;
maxGEN = 50000;
popSize = 1000; % 遗传算法种群大小
inputCrossoverProbabilty = 0.75;%0.75最优
crossoverProbabilty = inputCrossoverProbabilty; %交叉概率
inputProbabilty = 0.2;%0.1最好
maxProbabilty = 0.9;
mutationProbabilty = inputProbabilty; %变异概率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%存储最好的生成结果为最大值
gbest = Inf;
% 计算上述生成的城市距离
distances = calculateDistance(cities, ctype);
% 生成种群,每个个体代表一个路径 popSize*cityNum的矩阵
pop = zeros(popSize, cityNum);
%for i=1:popSize
% pop(i,:) = randperm(cityNum);
%end
pop = initParent(distances, cityNum,popSize);
offspring = zeros(popSize,cityNum);
%保存每代的最小路径便于画图
minPathes = zeros(maxGEN,1);
% GA算法
% 计算有多少次没更新最好权值了
count = 0;
lastgbest = 0;
countGen = 1;
flag = 0;
for gen=1:maxGEN
% sumDistance(n*1):总长度
[sumDistance] = newFitness(distances, pop);
[sortDistance, sortIndex] = sort(sumDistance);
% 保留上一代的最好结果
offspring(1,:) = pop(sortIndex(1),:);
minPath = sortDistance(1);
minPathes(gen,1) = minPath;
fprintf('代数:%d 最短路径:%.2fKM \n', gen,minPath);
for k=2:popSize
% 选择父代进行交叉 4*1
parent1Path = selectParent(sortIndex, pop, popSize);
parent2Path = selectParent(sortIndex, pop, popSize);
subPath = crossover(parent1Path, parent2Path, crossoverProbabilty);%交叉
subPath1 = mutate(subPath, mutationProbabilty);%变异
offspring(k,:) = subPath1(:);
end
% 更新
pop = offspring;
% 画出当前状态下的最短路径
if minPath < gbest
gbest = minPath;
countGen = gen;
flag = 1;
end
% 超过一定次数没有更新,就跳出
if gen - countGen > 1000
break;
end
%超过500次没更新就画图
if gen - countGen > 500 && flag == 1
paint(cities, pop, gbest, sumDistance, gen);
flag = 0;
end
%超过200次没更新就调整变异概率
if gen - countGen > 200
mutationProbabilty = maxProbabilty;
end
% if mutationProbabilty < 1
% mutationProbabilty = mutationProbabilty + 0.05;
% end
% if crossoverProbabilty < 0.8
% crossoverProbabilty = crossoverProbabilty + 0.05;
% end
% else
% %更新了就复原
% mutationProbabilty = inputProbabilty;
% crossoverProbabilty = inputCrossoverProbabilty;
% end
end
figure
plot(minPathes, 'MarkerFaceColor', 'red','LineWidth',1);
title('收敛曲线图(每一代的最短路径)');
set(gca,'ytick',500:100:5000);
ylabel('路径长度');
xlabel('迭代次数');
grid on
tEnd = toc(tStart);
fprintf('时间:%d 分 %f 秒.\n', floor(tEnd/60), rem(tEnd,60));
initparent——初始化
function pop = initParent(distances, cityNum,popSize)
pop = zeros(popSize, cityNum);
[row, col] = size(distances);
% 1/4*popSize 和 cityNum之间选最小的作为最优初始化的个数
% 为了保证选择前面50%的时候多样性还在
if(popSize / 4 > cityNum)
minLength = cityNum;
else
minLength = popSize / 4;
end
% 随机生成一个随机数数组作为开头
randomList = randperm(cityNum);
for k = 1:minLength
cityBest = zeros(1, cityNum);
flagList = zeros(1, cityNum);
%轮到第几行被遍历了
rowIndex = k;
%第k行的数字已经被使用了,不可以再使用
flagList(randomList(k)) = 1;
%第一个数字是randomList(k)
cityBest(1) = randomList(k);
%一共循环cityNum - 1
for i = 2:row
thisRow = distances(rowIndex, :);
best = Inf;
bestIndex = 1;
for j = 1:col
if thisRow(j) ~= 0 && thisRow(j) < best && flagList(j) == 0
best = thisRow(j);
bestIndex = j;
end
end
flagList(bestIndex) = 1;
rowIndex = bestIndex;
cityBest(i) = bestIndex;
end
pop(k, :) = cityBest;
end
%如果更大,证明还有一些种群要随机生成
for i=minLength + 1:popSize
pop(i,:) = randperm(cityNum);
end
end
crossver——重组
function [returnPath] = crossover(parent1Path, parent2Path, prob)
% 交叉
random = rand();
if prob >= random
[l, length] = size(parent1Path);
% 交叉后会生成两个子代
childPath = zeros(1,length);
flagPath = zeros(1, length);
% 交换的幅度是不超过一半
startIndex = randi(length);
%middleIndex = randi(length);
%middleIndex1 = randi(length);
endIndex = randi(length);
%list = [startIndex, endIndex, middleIndex, middleIndex1];
%list = sort(list);
%two = sort([startIndex, endIndex]);
count = 1;
for i = startIndex:endIndex
childPath(count) = parent1Path(i);
%flag上面为1,证明被使用了
flagPath(parent1Path(i)) = 1;
count = count + 1;
end
%for i = list(3):list(4)
% childPath(count) = parent1Path(i);
% %flag上面为1,证明被使用了
% flagPath(parent1Path(i)) = 1;
% count = count + 1;
%end
%赋值第二个父代的不同部分
for i = 1:length
if(flagPath(parent2Path(i)) == 1)
continue;
else
childPath(count) = parent2Path(i);
count = count + 1;
end
end
returnPath = childPath;
else
returnPath = parent1Path;
end
end
mutate——变异
function [ mutatedPath ] = mutate( path, prob)
%对指定的路径利用指定的概率进行更新
random = rand();
length1 = length(path);
%thisDistance = getDistance(path, distances);
% 概率->允许变异
if random <= prob
%for i = 1:10
index1 = randi(length1);
index2 = randi(length1);
%交换
temp = path(index1);
path(index1) = path(index2);
path(index2)=temp;
%end
end
mutatedPath = path;
end
paint——绘图
function [ output_args ] = paint( cities, pop, minPath, totalDistances,gen)
gNumber=gen;
[~, length] = size(cities);
xDots = cities(1,:);
yDots = cities(2,:);
%figure(1);
title('GA TSP');
plot(xDots,yDots, 'p', 'MarkerSize', 14, 'MarkerFaceColor', 'blue');
xlabel('经度');
ylabel('纬度');
axis equal
hold on
[minPathX,~] = find(totalDistances==minPath,1, 'first');
bestPopPath = pop(minPathX, :);
bestX = zeros(1,length);
bestY = zeros(1,length);
for j=1:length
bestX(1,j) = cities(1,bestPopPath(1,j));
bestY(1,j) = cities(2,bestPopPath(1,j));
end
bestX(1, length+1) = cities(1, bestPopPath(1, 1));
bestY(1, length+1) = cities(2, bestPopPath(1, 1));
title('GA TSP');
plot(bestX(1,:),bestY(1,:), 'red', 'LineWidth', 1.25);
legend('城市', '路径');
axis equal
grid on
%text(5,0,sprintf('迭代次数: %d 总路径长度: %.2f',gNumber, minPath),'FontSize',10);
drawnow
hold off
end
calculateDistance——距离分类与计算
function [ distances ] = calculateDistance( city, ctype )
%计算距离
if(strcmp(ctype, "ATT"))
[~, col] = size(city);
distances = zeros(col);
for i=1:col
for j=1:col
rij = sqrt( ((city(1,i)-city(1,j))^2 + (city(2,i)-city(2,j))^2) / 10);
tij = round(rij);
if tijgetDistance——距离获取
function distance = getDistance(path, distances)
col = length(path);
distance = distances(path(col),path(1));
for j=1:col-1
distance = distance + distances(path(j),path(j+1));
end
end
目前已知的最优解
- a280 : 2579
- ali535 : 202339
- att48 : 10628
- att532 : 27686
- bayg29 : 1610
- bays29 : 2020
- berlin52 : 7542
- bier127 : 118282
- brazil58 : 25395
- brd14051 : 469385
- brg180 : 1950
- burma14 : 3323
- ch130 : 6110
- ch150 : 6528
- d198 : 15780
- d493 : 35002
- d657 : 48912
- d1291 : 50801
- d1655 : 62128
- d2103 : 80450
- d15112 : 1573084
- d18512 : 645238
- dantzig42 : 699
- dsj1000 : 18659688 (EUC_2D)
- dsj1000 : 18660188 (CEIL_2D)
- eil51 : 426
- eil76 : 538
- eil101 : 629
- fl417 : 11861
- fl1400 : 20127
- fl1577 : 22249
- fl3795 : 28772
- fnl4461 : 182566
- fri26 : 937
- gil262 : 2378
- gr17 : 2085
- gr21 : 2707
- gr24 : 1272
- gr48 : 5046
- gr96 : 55209
- gr120 : 6942
- gr137 : 69853
- gr202 : 40160
- gr229 : 134602
- gr431 : 171414
- gr666 : 294358
- hk48 : 11461
- kroA100 : 21282
- kroB100 : 22141
- kroC100 : 20749
- kroD100 : 21294
- kroE100 : 22068
- kroA150 : 26524
- kroB150 : 26130
- kroA200 : 29368
- kroB200 : 29437
- lin105 : 14379
- lin318 : 42029
- linhp318 : 41345
- nrw1379 : 56638
- p654 : 34643
- pa561 : 2763
- pcb442 : 50778
- pcb1173 : 56892
- pcb3038 : 137694
- pla7397 : 23260728
- pla33810 : 66048945
- pla85900 : 142382641
- pr76 : 108159
- pr107 : 44303
- pr124 : 59030
- pr136 : 96772
- pr144 : 58537
- pr152 : 73682
- pr226 : 80369
- pr264 : 49135
- pr299 : 48191
- pr439 : 107217
- pr1002 : 259045
- pr2392 : 378032
- rat99 : 1211
- rat195 : 2323
- rat575 : 6773
- rat783 : 8806
- rd100 : 7910
- rd400 : 15281
- rl1304 : 252948
- rl1323 : 270199
- rl1889 : 316536
- rl5915 : 565530
- rl5934 : 556045
- rl11849 : 923288
- si175 : 21407
- si535 : 48450
- si1032 : 92650
- st70 : 675
- swiss42 : 1273
- ts225 : 126643
- tsp225 : 3916
- u159 : 42080
- u574 : 36905
- u724 : 41910
- u1060 : 224094
- u1432 : 152970
- u1817 : 57201
- u2152 : 64253
- u2319 : 234256
- ulysses16 : 6859
- ulysses22 : 7013
- usa13509 : 19982859
- vm1084 : 239297
- vm1748 : 336556
操作过的数据集情况
| 实验数据集 | 实验效果 | 最优解 | 百分比 |
|---|---|---|---|
| att48 | 10684 | 10628 | 99.5% |
| ch130 | 6212 | 6110 | 98.35% |
| a280 | 2725 | 2579 | 94.6% |
| att532 | 31143 | 27686 | 88.25% |
| dsj1000 | 21803908 | 18660188 | 85.5% |
| rl11849 | 1107708 | 923288 | 83.4% |
| usa13509 | 24826834 | 19982859 | 80.5% |
如果对你有帮助,欢迎转发收藏哦~
转发注明出处,感谢
最终代码打包地:https://download.csdn.net/download/a1303835514/14978704