机器人建模----运动学模型及代码实现
机器人建模----机械臂运动学模型及代码实现
- 经典DH参数法建模
-
- 建立DH坐标系
- 建立正运动学
- 建立雅克比矩阵
- 逆运动学
- UR逆运动学解析解
- 螺旋理论POE法建模
-
- 建立螺旋坐标系
- 建立正运动学
- 建立雅克比矩阵
- 代码实现
-
- 正运动学
- 雅克比矩阵
- UR逆运动学解析解
- 完整可用代码
机械臂的运动学模型,正运动学指已知机械臂关节位置、速度、加速度求机械臂末端工具位置、速度、加速度,反之称为逆运动学,其中正运动学相对容易,逆运动学求解比较困难。本文以6自由度机械臂UR为例做介绍,因7自由度机械臂与我毕业论文有重叠,故不再此处介绍,避免查重问题。下文将介绍两种机械臂建模方法,螺旋理论建模和DH参数法建模,并暂时提供DH参数建模的对应Python代码,若后续有精力,将提供基于螺旋理论的C++代码,如果只是想简单实用机械臂的正逆运动学,请参考KDL库实现机械臂运动学的方法PyKDL—正运动学和逆运动学。
经典DH参数法建模
建立DH坐标系
DH参数建模方法是最常用的串联机器人建模方法,采用 四个参数描述相邻连杆之间的运动学关系,当四个确定时,相邻连杆的位姿关系唯一确定。 DH参数法分为经典DH参数法和修正DH参数法,本文采用经典DH参数法。机械臂有n自由度,则需要建立n+1个坐标系,坐标系有多做建法,但坐标系建立后,其DH参数唯一确定。
UR5机械臂,对UR5建立DH坐标系如所示图 1,获得UR5的DH参数表如表1


建立正运动学
当机械臂的DH参数列表已知时,可以获得关节空间的关节角到末端操作空间的唯一对应关系。任意相邻连杆,其位姿关系可用齐次矩阵表示:

建立雅克比矩阵
雅克比矩阵可以看做速度级的正运动学传递矩阵,求逆可以获得速度级的逆运动学

逆运动学
UR逆运动学解析解
螺旋理论POE法建模
建立螺旋坐标系
旋量法建立机器人模型,只需要建立基坐标系和工具坐标系,其他关节用转动角度和运动螺旋表示,相对于DH法,更简洁。
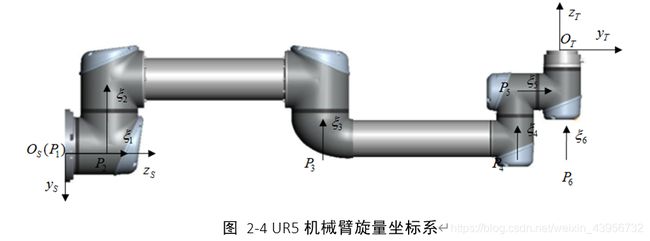

建立正运动学
建立雅克比矩阵
代码实现
正运动学
#=================相邻关节齐次变换矩阵=================#
def trans(theta,alpha,a,d):
'''
本函数用于求取n自由度机械臂正运动学
输入参数为DH参数,角度单位为rad,长度单位为mm
参数分别为theta,alpha,a,d,为0维常数值
返回齐次传递函数矩阵
'''
T = np.array([[math.cos(theta), -math.sin(theta)*math.cos(alpha), math.sin(theta)*math.sin(alpha), a*math.cos(theta)],
[math.sin(theta), math.cos(theta)*math.cos(alpha), -math.cos(theta)*math.sin(alpha), a*math.sin(theta)],
[0, math.sin(alpha), math.cos(alpha), d ],
[0, 0, 0, 1 ]])
return T
#输入某时刻对应的DH,返回齐次矩阵
def fkine(theta,alpha,a,d):
'''
本函数用于求取n自由度机械臂正运动学
输入参数为DH参数,角度单位为rad,长度单位为mm
参数分别为theta,alpha,a,d,为1维常数值
返回齐次传递函数矩阵
'''
#关节自由度
n = len(theta)
#建立4×4的齐次传递矩阵,定义为numpy类型
An = np.eye(4)
for i in range(n):
T = trans(theta[i],alpha[i],a[i],d[i])
An = np.dot(An,T) #末端到惯性坐标系传递矩阵
return An
雅克比矩阵
#构造法求雅克比矩阵,时间0.3ms
def jacobian(DH_0,qr):
'''
本函数用于求取机械臂的雅克比矩阵
input:DH_0参数,长度单位mm,角度单位red
qr,相对初始位置的转角
output:J,该位置点的雅克比矩阵
'''
n = len(qr)
theta = DH_0[:,0] + qr
alpha = DH_0[:,1]
a = DH_0[:,2]
d = DH_0[:,3]
#求取末端位置
An = fkine(theta,alpha,a,d) #正运动学函数
p_n = An[0:3,3]
J = np.zeros([6,n])
J[3:6,n-1] = An[0:3,2]
#求取其余转轴方向及位置点
Ai = np.eye(4)
for i in range(n-1):
z_i = Ai[0:3,2]
p_i = Ai[0:3,3]
p_in = p_n - p_i
J[0:3,i] = np.cross(z_i,p_in)
J[3:6,i] = z_i
Ai = np.dot(Ai, trans(theta[i], alpha[i], a[i], d[i]))
return J
#迭代雅可比,运行时间更快0.1ms
def jeco_0(DH_0, qr):
'''
本函数基于雅克比迭代求解n自由度机械臂逆运动学方程
input:DH_0 = [q_init,alpha,a,d];
q_ready是上一时刻的位置,单位:弧度;
T0e为DH坐标系确定的DH{0}坐标系与DH{6}之间的关系(目标矩阵);
efs求解误差阀值,默认值10^(-10)
i_limit迭代最大次数,默认值1000
output:qq为相对与DH_q0的转动角度,单位:弧度;已处理到[-pi, pi] 之间
'''
#建立初时刻迭代初值
q = DH_0[:,0] + qr
alpha = DH_0[:,1]
a = DH_0[:,2]
d = DH_0[:,3]
#计数及标签
n = len(q)
#计算雅克比矩阵
U = np.eye(4)
Jn = np.zeros([6,n])
T = np.zeros([4,4,n])
for i in range(n):
i = n - i - 1
T[:,:,i] = trans(q[i],alpha[i],a[i],d[i])
U = np.dot(T[:,:,i],U)
dd = np.array([-U[0,0]*U[1,3] + U[1,0]*U[0,3],
-U[0,1]*U[1,3] + U[1,1]*U[0,3],
-U[0,2]*U[1,3] + U[1,2]*U[0,3]])
Jn[0:3,i] = dd
Jn[3:6,i] = U[2,0:3]
An = fkine(q,alpha,a,d) #正运动学函数
R = An[0:3,0:3]
J_R = np.zeros([6,6])
J_R[0:3,0:3] = R
J_R[3:6,3:6] = R
J0 = np.dot(J_R,Jn)
return J0
UR逆运动学解析解
#=================UR构型解析解,DH坐标系需要满足要求=================#
#建立解ms+nc=d的求解函数
def mnsd(m,n,d):
'''
:param m:
:param n:
:param d:
:return:
'''
a = m**2 + n**2 -d**2
if(a<0):
print "不满足求解条件!"
return [0,0]
qq1 = np.arctan2(d/np.sqrt(m**2 + n**2), np.sqrt(1 - d**2/(m**2 + n**2))) \
- np.arctan2(n,m)
qq2 = np.arctan2(d / np.sqrt(m ** 2 + n ** 2), -np.sqrt(1 - d ** 2 / (m ** 2 + n ** 2))) \
- np.arctan2(n, m)
return [qq1,qq2]
#求解T1_inv*Te*T6_inv
def ttt(qq1,qq5,qq6,d1,d5,d6,Te):
'''
:param qq1:
:param qq5:
:param qq6:
:param d1:
:param d5:
:param d6:
:param Te:
:return:
'''
#求解T0_1的逆
T0_1_inv = np.array([[np.cos(qq1), np.sin(qq1), 0, 0],
[ 0, 0, 1, -d1],
[np.sin(qq1), -np.cos(qq1 ), 0, 0],
[ 0 , 0, 0, 1]])
T5_6_inv = np.array([[np.cos(qq6), np.sin(qq6), 0, 0],
[-np.sin(qq6), np.cos(qq6), 0, 0],
[ 0, 0, 1, -d6],
[ 0, 0, 0, 1]])
T4_5_inv = np.array([[np.cos(qq5), np.sin(qq5), 0, 0],
[ 0, 0, -1, d5],
[-np.sin(qq5), np.cos(qq5), 0, 0],
[ 0, 0, 0, 1]])
A = np.dot(np.dot(np.dot(T0_1_inv,Te),T5_6_inv),T4_5_inv)
return A
#求解关节角234
def theta234(A,a2,a3):
'''
:param A:
:param a2:
:param a3:
:param d5:
:return:
'''
#求关节角3
h = (np.power(A[0,3], 2) + np.power(A[1,3], 2) - np.power(a2, 2) - np.power(a3, 2)) / (2 * a2*a3)
qq3_1 = math.acos(h)
qq3_2 = -math.acos(h)
#求关节角2
s2_1 = ((a3 * math.cos(qq3_1) + a2) * A[1, 3] - a3 * math.sin(qq3_1) * A[0, 3]) / \
(a2 ** 2 + a3 ** 2 + 2 * a2 * a3 * math.cos(qq3_1))
c2_1 = (A[0, 3] + a3 * math.sin(qq3_1) * s2_1) / (a3 * math.cos(qq3_1) + a2)
s2_2 = ((a3 * math.cos(qq3_2) + a2) * A[1, 3] - a3 * math.sin(qq3_2) * A[0, 3]) / \
(a2 ** 2 + a3 ** 2 + 2 * a2 * a3 * math.cos(qq3_2))
c2_2 = (A[0, 3] + a3 * math.sin(qq3_2) * s2_2) / (a3 * math.cos(qq3_2) + a2)
qq2_1 = math.atan2(s2_1, c2_1)
qq2_2= math.atan2(s2_2, c2_2)
#关节角4
qq_234 = math.atan2(A[1, 0], A[0, 0])
qq4_1 = qq_234 - qq2_1 - qq3_1
qq4_2 = qq_234 - qq2_2 - qq3_2
return [[qq2_1, qq3_1, qq4_1], [qq2_2, qq3_2, qq4_2]]
#采用看解析发求逆
def ur_ikine(DH_0,Te):
'''
:param DH: 按theta\alpha\a\d排列
:param Te: n,o,a,p排列
:return:
'''
#获取DH参数
d1 = DH_0[0, 3]
a2 = DH_0[1, 2]
a3 = DH_0[2, 2]
d4 = DH_0[3, 3]
d5 = DH_0[4, 3]
d6 = DH_0[5, 3]
#******************求解关节1******************#
#中间参数
m1 = Te[0,3] - d6*Te[0,2]
n1 = d6*Te[1,2] - Te[1,3]
#求取关节角,第二个数值代表关节角1对应两组解的编号
[qq1_1,qq1_2] = mnsd(m1, n1, d4)
# ******************求解关节5******************#
# 中间参数
m5_1 = np.sin(qq1_1) * Te[0, 2] - np.cos(qq1_1) * Te[1, 2]
m5_2 = np.sin(qq1_2) * Te[0, 2] - np.cos(qq1_2) * Te[1, 2]
#求取关节角,第三个数值代表关节角5对应两组解的编号
qq5_1_1 = np.arctan2(np.sqrt(1 - m5_1 ** 2), m5_1)
qq5_1_2 = np.arctan2(-np.sqrt(1 - m5_1 ** 2), m5_1)
qq5_2_1 = np.arctan2(np.sqrt(1 - m5_2 ** 2), m5_2)
qq5_2_2 = np.arctan2(-np.sqrt(1 - m5_2 ** 2), m5_2)
# ******************求解关节6******************#
# 中间参数
m6_1 = -np.sin(qq1_1) * Te[0, 1] + np.cos(qq1_1) * Te[1, 1]
n6_1 = np.sin(qq1_1) * Te[0, 0] - np.cos(qq1_1) * Te[1, 0]
m6_2 = -np.sin(qq1_2) * Te[0, 1] + np.cos(qq1_2) * Te[1, 1]
n6_2 = np.sin(qq1_2) * Te[0, 0] - np.cos(qq1_2) * Te[1, 0]
# 求取关节角
qq6_1_1 = np.arctan2(np.sin(qq5_1_1), 0) - np.arctan2(n6_1, m6_1)
qq6_1_2 = np.arctan2(np.sin(qq5_1_2), 0) - np.arctan2(n6_1, m6_1)
qq6_2_1 = np.arctan2(np.sin(qq5_2_1), 0) - np.arctan2(n6_2, m6_2)
qq6_2_2 = np.arctan2(np.sin(qq5_2_2), 0) - np.arctan2(n6_2, m6_2)
# ******************求解关节2,3,4******************#
# 中间参数
A_1_1 = ttt(qq1_1,qq5_1_1, qq6_1_1, d1, d5, d6, Te)
A_1_2 = ttt(qq1_1,qq5_1_2, qq6_1_2, d1, d5, d6, Te)
A_2_1 = ttt(qq1_2,qq5_2_1, qq6_2_1, d1, d5, d6, Te)
A_2_2 = ttt(qq1_2,qq5_2_2, qq6_2_2, d1, d5, d6, Te)
# 求取关节角,第四个数值代表关节角2对应两组解的编号
[qq234_1_1_1, qq234_1_1_2] = theta234(A_1_1, a2, a3)
[qq234_1_2_1, qq234_1_2_2] = theta234(A_1_2, a2, a3)
[qq234_2_1_1, qq234_2_1_2] = theta234(A_2_1, a2, a3)
[qq234_2_2_1, qq234_2_2_2] = theta234(A_2_2, a2, a3)
# ******************组建8组解******************#
qq = np.array([[qq1_1, qq234_1_1_1[0], qq234_1_1_1[1], qq234_1_1_1[2], qq5_1_1, qq6_1_1],
[qq1_1, qq234_1_1_2[0], qq234_1_1_2[1], qq234_1_1_2[2], qq5_1_1, qq6_1_1],
[qq1_1, qq234_1_2_1[0], qq234_1_2_1[1], qq234_1_2_1[2], qq5_1_2, qq6_1_2],
[qq1_1, qq234_1_2_2[0], qq234_1_2_2[1], qq234_1_2_2[2], qq5_1_2, qq6_1_2],
[qq1_2, qq234_2_1_1[0], qq234_2_1_1[1], qq234_2_1_1[2], qq5_2_1, qq6_2_1],
[qq1_2, qq234_2_1_2[0], qq234_2_1_2[1], qq234_2_1_2[2], qq5_2_1, qq6_2_1],
[qq1_2, qq234_2_2_1[0], qq234_2_2_1[1], qq234_2_2_1[2], qq5_2_2, qq6_2_2],
[qq1_2, qq234_2_2_2[0], qq234_2_2_2[1], qq234_2_2_2[2], qq5_2_2, qq6_2_2]])
#print "qq:\n",np.around(qq*180/pi)
#将求解范围转换到[-pi,pi]
Q = np.zeros([8,6])
for i in range(8):
qq[i, :] = qq[i,:] - DH_0[:, 0]
Q[i,:] = bf.qq_choose(qq[i,:])
#print "Q:\n", np.around(Q * 180 / pi)
return Q
#求解唯一解的ur解析解,时间为0.5ms
def ur_ikine_choice(DH_0,Te,qq_k):
'''
:param DH: DH参数
:param Te: 末端齐次位姿
:param qq_k: 上一时刻关节角
:return:
'''
#求取8组解
Q = ur_ikine(DH_0, Te)
#调用选择函数求取最佳关节角
qq = bf.qq_eight_choice(Q, qq_k)
return qq
完整可用代码
#!/usr/bin/env python
#-*-coding:utf-8-*-
#本文档用于求7自由度SRS型机械臂运动学相关函数
#程序员:陈永**
#版权:哈尔滨工业大学(深圳)
#日期:初稿:2019.9.20
import numpy as np
import numpy.linalg as nla
import math
from math import pi
#导入自定义函数
import BaseFunction as bf
#UR5机械臂
#=================相邻关节齐次变换矩阵=================#
def trans(theta,alpha,a,d):
'''
本函数用于求取n自由度机械臂正运动学
输入参数为DH参数,角度单位为rad,长度单位为mm
参数分别为theta,alpha,a,d,为0维常数值
返回齐次传递函数矩阵
'''
T = np.array([[math.cos(theta), -math.sin(theta)*math.cos(alpha), math.sin(theta)*math.sin(alpha), a*math.cos(theta)],
[math.sin(theta), math.cos(theta)*math.cos(alpha), -math.cos(theta)*math.sin(alpha), a*math.sin(theta)],
[0, math.sin(alpha), math.cos(alpha), d ],
[0, 0, 0, 1 ]])
return T
#================建立n自由度机械臂正运动学==============#
#输入某时刻对应的DH,返回齐次矩阵
def fkine(theta,alpha,a,d):
'''
本函数用于求取n自由度机械臂正运动学
输入参数为DH参数,角度单位为rad,长度单位为mm
参数分别为theta,alpha,a,d,为1维常数值
返回齐次传递函数矩阵
'''
#关节自由度
n = len(theta)
#建立4×4的齐次传递矩阵,定义为numpy类型
An = np.eye(4)
for i in range(n):
T = trans(theta[i],alpha[i],a[i],d[i])
An = np.dot(An,T) #末端到惯性坐标系传递矩阵
return An
#输入初始时刻DH_0和相对转角,输出六维末端位姿
def fkine_euler(DH_0,qr):
'''
本函数用于求取n自由度机械臂正运动学
输入参数为DH参数,角度单位为rad,长度单位为mm
参数分别为theta,alpha,a,d,为1维常数值
返回齐次传递函数矩阵
'''
#DH参数
theta = DH_0[:, 0] + qr
alpha = DH_0[:, 1]
a = DH_0[:, 2]
d = DH_0[:, 3]
#关节自由度
n = len(theta)
xe = np.zeros(6)
#建立4×4的齐次传递矩阵,定义为numpy类型
An = np.eye(4)
for i in range(n):
T = trans(theta[i],alpha[i],a[i],d[i])
An = np.dot(An,T) #末端到惯性坐标系传递矩阵
xe[0:3] = An[0:3,3]
xe[3:6] = bf.rot2euler_zyx(An[0:3,0:3])
return xe
#=====================求雅克比矩阵====================#
#构造法求雅克比矩阵,时间0.3ms
def jacobian(DH_0,qr):
'''
本函数用于求取机械臂的雅克比矩阵
input:DH_0参数,长度单位mm,角度单位red
qr,相对初始位置的转角
output:J,该位置点的雅克比矩阵
'''
n = len(qr)
theta = DH_0[:,0] + qr
alpha = DH_0[:,1]
a = DH_0[:,2]
d = DH_0[:,3]
#求取末端位置
An = fkine(theta,alpha,a,d)
p_n = An[0:3,3]
J = np.zeros([6,n])
J[3:6,n-1] = An[0:3,2]
#求取其余转轴方向及位置点
Ai = np.eye(4)
for i in range(n-1):
z_i = Ai[0:3,2]
p_i = Ai[0:3,3]
p_in = p_n - p_i
J[0:3,i] = np.cross(z_i,p_in)
J[3:6,i] = z_i
Ai = np.dot(Ai, trans(theta[i], alpha[i], a[i], d[i]))
return J
#迭代雅可比,运行时间更快0.1ms
def jeco_0(DH_0, qr):
'''
本函数基于雅克比迭代求解n自由度机械臂逆运动学方程
input:DH_0 = [q_init,alpha,a,d];
q_ready是上一时刻的位置,单位:弧度;
T0e为DH坐标系确定的DH{0}坐标系与DH{6}之间的关系(目标矩阵);
efs求解误差阀值,默认值10^(-10)
i_limit迭代最大次数,默认值1000
output:qq为相对与DH_q0的转动角度,单位:弧度;已处理到[-pi, pi] 之间
'''
#建立初时刻迭代初值
q = DH_0[:,0] + qr
alpha = DH_0[:,1]
a = DH_0[:,2]
d = DH_0[:,3]
#计数及标签
n = len(q)
#计算雅克比矩阵
U = np.eye(4)
Jn = np.zeros([6,n])
T = np.zeros([4,4,n])
for i in range(n):
i = n - i - 1
T[:,:,i] = trans(q[i],alpha[i],a[i],d[i])
U = np.dot(T[:,:,i],U)
dd = np.array([-U[0,0]*U[1,3] + U[1,0]*U[0,3],
-U[0,1]*U[1,3] + U[1,1]*U[0,3],
-U[0,2]*U[1,3] + U[1,2]*U[0,3]])
Jn[0:3,i] = dd
Jn[3:6,i] = U[2,0:3]
An = fkine(q,alpha,a,d)
R = An[0:3,0:3]
J_R = np.zeros([6,6])
J_R[0:3,0:3] = R
J_R[3:6,3:6] = R
J0 = np.dot(J_R,Jn)
return J0
#=================UR构型解析解,DH坐标系需要满足要求=================#
#建立解ms+nc=d的求解函数
def mnsd(m,n,d):
'''
:param m:
:param n:
:param d:
:return:
'''
a = m**2 + n**2 -d**2
if(a<0):
print "不满足求解条件!"
return [0,0]
qq1 = np.arctan2(d/np.sqrt(m**2 + n**2), np.sqrt(1 - d**2/(m**2 + n**2))) \
- np.arctan2(n,m)
qq2 = np.arctan2(d / np.sqrt(m ** 2 + n ** 2), -np.sqrt(1 - d ** 2 / (m ** 2 + n ** 2))) \
- np.arctan2(n, m)
return [qq1,qq2]
#求解T1_inv*Te*T6_inv
def ttt(qq1,qq5,qq6,d1,d5,d6,Te):
'''
:param qq1:
:param qq5:
:param qq6:
:param d1:
:param d5:
:param d6:
:param Te:
:return:
'''
#求解T0_1的逆
T0_1_inv = np.array([[np.cos(qq1), np.sin(qq1), 0, 0],
[ 0, 0, 1, -d1],
[np.sin(qq1), -np.cos(qq1 ), 0, 0],
[ 0 , 0, 0, 1]])
T5_6_inv = np.array([[np.cos(qq6), np.sin(qq6), 0, 0],
[-np.sin(qq6), np.cos(qq6), 0, 0],
[ 0, 0, 1, -d6],
[ 0, 0, 0, 1]])
T4_5_inv = np.array([[np.cos(qq5), np.sin(qq5), 0, 0],
[ 0, 0, -1, d5],
[-np.sin(qq5), np.cos(qq5), 0, 0],
[ 0, 0, 0, 1]])
A = np.dot(np.dot(np.dot(T0_1_inv,Te),T5_6_inv),T4_5_inv)
return A
#求解关节角234
def theta234(A,a2,a3):
'''
:param A:
:param a2:
:param a3:
:param d5:
:return:
'''
#求关节角3
h = (np.power(A[0,3], 2) + np.power(A[1,3], 2) - np.power(a2, 2) - np.power(a3, 2)) / (2 * a2*a3)
qq3_1 = math.acos(h)
qq3_2 = -math.acos(h)
#求关节角2
s2_1 = ((a3 * math.cos(qq3_1) + a2) * A[1, 3] - a3 * math.sin(qq3_1) * A[0, 3]) / \
(a2 ** 2 + a3 ** 2 + 2 * a2 * a3 * math.cos(qq3_1))
c2_1 = (A[0, 3] + a3 * math.sin(qq3_1) * s2_1) / (a3 * math.cos(qq3_1) + a2)
s2_2 = ((a3 * math.cos(qq3_2) + a2) * A[1, 3] - a3 * math.sin(qq3_2) * A[0, 3]) / \
(a2 ** 2 + a3 ** 2 + 2 * a2 * a3 * math.cos(qq3_2))
c2_2 = (A[0, 3] + a3 * math.sin(qq3_2) * s2_2) / (a3 * math.cos(qq3_2) + a2)
qq2_1 = math.atan2(s2_1, c2_1)
qq2_2= math.atan2(s2_2, c2_2)
#关节角4
qq_234 = math.atan2(A[1, 0], A[0, 0])
qq4_1 = qq_234 - qq2_1 - qq3_1
qq4_2 = qq_234 - qq2_2 - qq3_2
return [[qq2_1, qq3_1, qq4_1], [qq2_2, qq3_2, qq4_2]]
#采用看解析发求逆
def ur_ikine(DH_0,Te):
'''
:param DH: 按theta\alpha\a\d排列
:param Te: n,o,a,p排列
:return:
'''
#获取DH参数
d1 = DH_0[0, 3]
a2 = DH_0[1, 2]
a3 = DH_0[2, 2]
d4 = DH_0[3, 3]
d5 = DH_0[4, 3]
d6 = DH_0[5, 3]
#******************求解关节1******************#
#中间参数
m1 = Te[0,3] - d6*Te[0,2]
n1 = d6*Te[1,2] - Te[1,3]
#求取关节角,第二个数值代表关节角1对应两组解的编号
[qq1_1,qq1_2] = mnsd(m1, n1, d4)
# ******************求解关节5******************#
# 中间参数
m5_1 = np.sin(qq1_1) * Te[0, 2] - np.cos(qq1_1) * Te[1, 2]
m5_2 = np.sin(qq1_2) * Te[0, 2] - np.cos(qq1_2) * Te[1, 2]
#求取关节角,第三个数值代表关节角5对应两组解的编号
qq5_1_1 = np.arctan2(np.sqrt(1 - m5_1 ** 2), m5_1)
qq5_1_2 = np.arctan2(-np.sqrt(1 - m5_1 ** 2), m5_1)
qq5_2_1 = np.arctan2(np.sqrt(1 - m5_2 ** 2), m5_2)
qq5_2_2 = np.arctan2(-np.sqrt(1 - m5_2 ** 2), m5_2)
# ******************求解关节6******************#
# 中间参数
m6_1 = -np.sin(qq1_1) * Te[0, 1] + np.cos(qq1_1) * Te[1, 1]
n6_1 = np.sin(qq1_1) * Te[0, 0] - np.cos(qq1_1) * Te[1, 0]
m6_2 = -np.sin(qq1_2) * Te[0, 1] + np.cos(qq1_2) * Te[1, 1]
n6_2 = np.sin(qq1_2) * Te[0, 0] - np.cos(qq1_2) * Te[1, 0]
# 求取关节角
qq6_1_1 = np.arctan2(np.sin(qq5_1_1), 0) - np.arctan2(n6_1, m6_1)
qq6_1_2 = np.arctan2(np.sin(qq5_1_2), 0) - np.arctan2(n6_1, m6_1)
qq6_2_1 = np.arctan2(np.sin(qq5_2_1), 0) - np.arctan2(n6_2, m6_2)
qq6_2_2 = np.arctan2(np.sin(qq5_2_2), 0) - np.arctan2(n6_2, m6_2)
# ******************求解关节2,3,4******************#
# 中间参数
A_1_1 = ttt(qq1_1,qq5_1_1, qq6_1_1, d1, d5, d6, Te)
A_1_2 = ttt(qq1_1,qq5_1_2, qq6_1_2, d1, d5, d6, Te)
A_2_1 = ttt(qq1_2,qq5_2_1, qq6_2_1, d1, d5, d6, Te)
A_2_2 = ttt(qq1_2,qq5_2_2, qq6_2_2, d1, d5, d6, Te)
# 求取关节角,第四个数值代表关节角2对应两组解的编号
[qq234_1_1_1, qq234_1_1_2] = theta234(A_1_1, a2, a3)
[qq234_1_2_1, qq234_1_2_2] = theta234(A_1_2, a2, a3)
[qq234_2_1_1, qq234_2_1_2] = theta234(A_2_1, a2, a3)
[qq234_2_2_1, qq234_2_2_2] = theta234(A_2_2, a2, a3)
# ******************组建8组解******************#
qq = np.array([[qq1_1, qq234_1_1_1[0], qq234_1_1_1[1], qq234_1_1_1[2], qq5_1_1, qq6_1_1],
[qq1_1, qq234_1_1_2[0], qq234_1_1_2[1], qq234_1_1_2[2], qq5_1_1, qq6_1_1],
[qq1_1, qq234_1_2_1[0], qq234_1_2_1[1], qq234_1_2_1[2], qq5_1_2, qq6_1_2],
[qq1_1, qq234_1_2_2[0], qq234_1_2_2[1], qq234_1_2_2[2], qq5_1_2, qq6_1_2],
[qq1_2, qq234_2_1_1[0], qq234_2_1_1[1], qq234_2_1_1[2], qq5_2_1, qq6_2_1],
[qq1_2, qq234_2_1_2[0], qq234_2_1_2[1], qq234_2_1_2[2], qq5_2_1, qq6_2_1],
[qq1_2, qq234_2_2_1[0], qq234_2_2_1[1], qq234_2_2_1[2], qq5_2_2, qq6_2_2],
[qq1_2, qq234_2_2_2[0], qq234_2_2_2[1], qq234_2_2_2[2], qq5_2_2, qq6_2_2]])
#print "qq:\n",np.around(qq*180/pi)
#将求解范围转换到[-pi,pi]
Q = np.zeros([8,6])
for i in range(8):
qq[i, :] = qq[i,:] - DH_0[:, 0]
Q[i,:] = bf.qq_choose(qq[i,:])
#print "Q:\n", np.around(Q * 180 / pi)
return Q
#求解唯一解的ur解析解,时间为0.5ms
def ur_ikine_choice(DH_0,Te,qq_k):
'''
:param DH: DH参数
:param Te: 末端齐次位姿
:param qq_k: 上一时刻关节角
:return:
'''
#求取8组解
Q = ur_ikine(DH_0, Te)
#调用选择函数求取最佳关节角
qq = bf.qq_eight_choice(Q, qq_k)
return qq
调用的函数:BaseFunction.py
#!/usr/bin/env python
#-*-coding:utf-8-*-
#本文档用于规划中的末端轨迹求取,默认等时间取样
#程序员:陈永*
#版权:哈尔滨工业大学(深圳)
#日期:初稿:2019.11.26
import numpy as np
import math
from math import pi
解析解8选一算法
def qq_eight_choice(Q,qq_k):
'''
:param Q: 8组关节角,行排列
:param qq_k: 上一时刻关节角
:return:
'''
#定义当前关节角与上一时刻关节角的距离
delta_l = np.zeros(8)
#求取每组关节角与上一时刻关节角的距离
for i in range(8):
qq = Q[i, :]
delta_qq = qq - qq_k
delta_l[i] = nla.norm(delta_qq)
l_min_k = np.argmin(delta_l)
qq_choice =Q[l_min_k,:]
return qq_choice
#将关节角计算到正负pi
def qq_choose(qq):
'''
本函数用于选着关节角范围
input:qq为计算出的关节角
output:q关节角范围[-pi,pi]
'''
n = len(qq)
q = np.copy(qq)
for i in range(n):
while (q[i] > pi):
q[i] = q[i] - 2*pi
while (q[i] < - pi):
q[i] = q[i] + 2*pi
return q



