Python数据分析之特征处理笔记六——特征预处理（案例分析）

摘要：阅读了前面文章的小伙伴们有没有对特征预处理有了一定的了解呢？接下来这篇文章将通过一个分析实践项目进一步了解特征预处理的过程。

目录

1. 特征预处理

1.1 获取数据，数据清洗

1.2 确定标注

 1.3 特征变换

1.3.1 Z-score标准化与最大最小标准化

 1.3.2 标签法和独热法

 1.4 特征降维

2. 模型建立

---

数据来源：本文的数据及代码来源于B站up主，Python数据分析-数据挖掘教程_哔哩哔哩_bilibili

 需要本文数据或者有疑问的伙伴也可私信我，我们一起交流。

项目思路：

• 获取数据，确定标注
• 数据清洗，主要就是处理空值及异常值
• 特征选择，若数据特征不多建议不用特征选择
• 特征变换，常用标准化、归一化、数值化方法
• 特征降维，使用较为高效的主成分分析法

需要注意的是如果我们先确定标注在进行数据清洗的话会导致标注的维度与特征的维度会出现不一致的情况，所以我们可以找到标注，先让电脑进行数据清洗统一工作，然后再让电脑提取标注，保证标注与特征的维度一样。

1. 特征预处理

1.1 获取数据，数据清洗

import pandas as pd 
df=pd.read_csv('D:/数据分析/HR.csv')
print(df)

 提供数据的up主为了让大家方便学习，就制造了这样一个数据集，并将异常值和空值放在数据集的最后面，在此感谢up主。观察数据集，满意度水平（satisfaction_level）有空值出现，最近评价（last_evalution）和工资（salary）有异常值出现，接下来就需要处理这些数据。

#1.清洗数据 
df=df.dropna(subset=['satisfaction_level','last_evaluation'])
df=df[df['satisfaction_level']<=1][df['last_evaluation']<=1][df['salary']!='nme']
print(df)

 这样就得到了经过简单处理的数据，在数据较多的情况下，我们还可以利用前面文章说过的分位数来得到分析数据，也可以通过特殊值填充等方法来处理。

1.2 确定标注

将是否离职（left）视为标注，并将其从数据集中提取出来

#2.得到标注
label=df['left']
df=df.drop('left',axis=1)
# 先清洗数据再取标注，可以使最后数据和标注行数一样，如果先取标注再清洗的话，最后结果的行数就不一样

#3.特征选择：在此暂不用特征选择，因为获取的数据较少

 1.3 特征变换

观察经过清洗的数据集，发现除了工资（salary）和部门（department）是非数值型数据外，其他的数据均为数值型数据，那么特征变换就需要分为两部分来进行。首先进行数值型数据的特征变换，采用Z-score标准化和最大最小标准化两种方法。

思路是：为每个特征设定一个参数值，参数值可以指定该特征是进行Z-score标准化还是最大最小标准化处理。

1.3.1 Z-score标准化与最大最小标准化

我们设定的参数如下：

以sl为例，如果参数是False的话，那么特征satisfaction_level就用最大最小标准化，如果是True的话就用z-score标准化。其他特征也是如此。

sl:satisfaction_level--False:MinMaxScaler;True:StandardScaler
le:last_evalution--False:MinMaxScaler;True:StandardScaler
npr:number_project--False:MinMaxScaler;True:StandardScaler
amh:average_monthly_hours--False:MinMaxScaler;True:StandardScaler
tsc:time_spend_company--False:MinMaxScaler;True:StandardScaler
wa:work_accident--False:MinMaxScaler;True:StandardScaler
pl5:promotion_last_5years--False:MinMaxScaler;True:StandardScaler

回忆前面所学的内容：

最大最小标准化又称为离差标准化，使结果映射到[0,1]之间，比较适用在数值比较集中的情况。

Z-score标准化要求原始数据的分布可以近似为正态分布，否则归一化的效果会变得很糟糕。

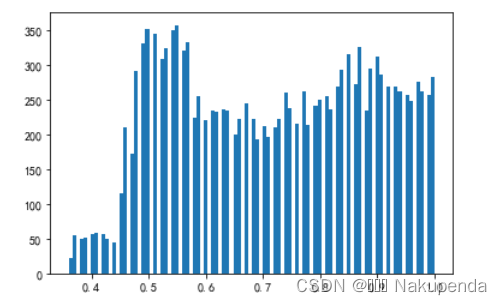
我们直接用直方图来看一下不同特征的数据情况，首先工作事故（work_accident）和近5年升职情况（promotion_last_5years）只有0和1两个值，可以进行最大最小标准化，逐个运行plt函数。

import matplotlib.pyplot as plt
plt.hist(df['satisfaction_level'],bins=100)
#plt.hist(df['last_evaluation'],bins=100)
#plt.hist(df['number_project'],bins=100)
#plt.hist(df['average_monthly_hours'],bins=100)
#plt.hist(df['time_spend_company'],bins=100)
#plt.hist(df['Work_accident'],bins=2)
#plt.hist(df['promotion_last_5years'],bins=2)

 

 

 

from sklearn.preprocessing import MinMaxScaler,StandardScaler
def Z_minmax(sl=False,le=False,npr=True,amh=False,tsc=False,wa=False,pl5=False):
    scaler_lst=[sl,le,npr,amh,tsc,wa,pl5]
    column_lst=['satisfaction_level','last_evaluation','number_project','average_monthly_hours','time_spend_company','Work_accident','promotion_last_5years']
    for i in range(len(scaler_lst)):
        if scaler_lst[i]:
            df[column_lst[i]]=StandardScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(-1,1)
        else:
            df[column_lst[i]]=MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(-1,1)
    return df,label
Z_minmax()

 1.3.2 标签法和独热法

与上面过程一样，我们设定的参数如下：

False时表示采用标签法，True时表示采用独热法，根据经验，我们对salary用标签法，对department用独热法。

dp:department--False:LabelEncoding;True:OneHotEncoding
slr:salary--False:LabelEncoding;True:OneHotEncoding

from sklearn.preprocessing import LabelEncoder,OneHotEncoder
def label_onehot(slr=True,dp=False):
    df1,lable=Z_minmax()
    scaler_lst=[slr,dp]
    column_lst=['salary','department']
    for i in range(len(scaler_lst)):
        if scaler_lst[i]:
            if column_lst[i]=="salary":
                df1[column_lst[i]]=[map_salary(s) for s in df1['salary'].values]
                #salary为定序数据，可以通过标签法赋值，但会根据首字母排序赋值，通过下面的map_salary函数给它赋值
            else:
                df1[column_lst[i]]=LabelEncoder().fit_transform(df1[column_lst[i]])
            df1[column_lst[i]]=MinMaxScaler().fit_transform(df1[column_lst[i]].values.reshape(-1,1)).reshape(-1,1)
            #数值化定类数据和定序数据以后，可通过归一法规范数据
        else:
            df1=pd.get_dummies(df1,columns=[column_lst[i]])
            #也可选择用OneHot处理，但用OneHot比较费力，需要把所有的类别提取来进行标签化后再进行独热。可用比较方便的get_dummies方法处理
    return df1,lable
d=dict([('low',0),('medium',1),('high',2)])
def map_salary(s):
    return d.get(s,0)
    #给上面函数中的salary赋值，没有找到时默认为0，即低收入人群
label_onehot()

 

 1.4 特征降维

前面提到：PCA方法比较简单，只需要计算方差以衡量信息量，不会受外部因素的影响。同时主成分之间相互正交，可消除原始数据集之间相互影响的因素。但PCA方法对于主成分的解释具有模糊性，且有会删除一些方差虽然小但比较重要的数据，可能会造成模型的过拟合。

若我们想要直接得到降维后的数据，用几个主成分表示我们得到的大部分信息，直接使用主成分（PCA）法就可以，代码如下：

from sklearn.decomposition import PCA
def PCA_method(lower_d=True,ld_n=3):
    df2,label2=label_onehot()
    if lower_d:
        return PCA(n_components=ld_n).fit_transform(df2.values)
    # return LinearDiscriminantAnalysis(n_components=ld_n)
    # 注意，n_components的值不能大于类的个数，因选择的标注只有0和1两类，不管n_components填多少，降维以后都是1维，则
    # 不考虑用LDA进行降维,用PCA降维,PCA降维可以不使用标注
PCA_method()

 好啦，以上就是一个简单的特征处理过程，接下来我们可以用数据来建立一个监督学习的模型。

2. 模型建立

下面我们建立一个KNN模型，该算法的思想是：每个数据集都有标注，如果一个点的k个最近的邻居，邻居中的一种标注的数量大于另一种标注的，那么该点倾向于与标注更多的邻居是一致的。

def get_model():
    features,label2=label_onehot()
    from sklearn.model_selection import train_test_split
    f_v=features.values
    l_v=label.values
    X_tt,X_validation,Y_tt,Y_validation=train_test_split(f_v,l_v,test_size=0.2)
    X_train,X_test,Y_train,Y_test=train_test_split(X_tt,Y_tt,test_size=0.25)
    print(len(X_train),len(X_validation),len(X_test))
    #利用N折交叉验证法进行模型验证
    from sklearn.neighbors import NearestNeighbors,KNeighborsClassifier
    #NearestNeighbors可直接得到一个点附近最近的几个点
    
    knn_clf=KNeighborsClassifier(n_neighbors=3)
    #n_neighbors=5时是否是一个有效的值呢，可以改变它的值进行运算，观察最后的三个值是否升高，得出等于3时三个值较大
    knn_clf_n5=KNeighborsClassifier(n_neighbors=5)
    #为了更有说服力，建立第二个模型判断哪个值更有效
    
    knn_clf.fit(X_train,Y_train)
    knn_clf_n5.fit(X_train,Y_train)
    Y_pred=knn_clf.predict(X_validation)
    Y_pred_n5=knn_clf_n5.predict(X_validation)
    #得到X验证集在K近邻法下的标注预测数据，接下来进行衡量
    
    
    from sklearn.metrics import accuracy_score,recall_score,f1_score
    #用以上三个指标进行预测值和实际值之间的衡量
    
    #验证集验证
    print('验证集：')
    print('ACC:',accuracy_score(Y_validation,Y_pred))
    print("REC:",recall_score(Y_validation,Y_pred)) #召回率
    print("F_score:",f1_score(Y_validation,Y_pred)) #F值
    
#     print('ACC:',accuracy_score(Y_validation,Y_pred_n5))
#     print("REC:",recall_score(Y_validation,Y_pred_n5)) #召回率
#     print("F_score:",f1_score(Y_validation,Y_pred_n5)) #F值
#     通过比较，显示3更有效
   Y_pred_add=knn_clf.predict(X_train)
    #进一步对训练集进行预测，相应的Y_validatio改为Y_train,Y_pred改为Y_pred_add
    #训练集验证
    print('训练集：')
    print('ACC:',accuracy_score(Y_train,Y_pred_add))
    print("REC:",recall_score(Y_train,Y_pred_add)) #召回率
    print("F_score:",f1_score(Y_train,Y_pred_add)) #F值
    
    Y_pred=knn_clf.predict(X_test)
    #测试集验证
    print('测试集')
    print('ACC:',accuracy_score(Y_test,Y_pred))
    print("REC:",recall_score(Y_test,Y_pred)) #召回率
    print("F_score:",f1_score(Y_test,Y_pred)) #F值
    #验证完毕后可修改hr_preprocessing函数里的参数值训练模型，得到更加令人满意的结果
    
    #训练出一个模型不容易，需要对其进行存储
    from sklearn.externals import joblib
    joblib.dump(knn_clf,"knn_clf")
    #存储模型
    knn_clf=joblib.load('knn_clf')
    #使用模型
    Y_pred=knn_clf.predict(X_test)
    print('测试集2')
    print('ACC:',accuracy_score(Y_test,Y_pred))
    print("REC:",recall_score(Y_test,Y_pred)) #召回率
    print("F_score:",f1_score(Y_test,Y_pred)) #F值
get_model()

 观察最后得出的结果，可以看到有一点过拟合的情况，过拟合主要是有两个原因造成的：数据太少+模型太复杂。所以，我们可以通过使用合适复杂度的模型来防止过拟合问题，让其足够拟合真正的规则，同时又不至于拟合太多抽样误差。 要解决过拟合的问题有几种方法：

• 增加数据量，我们可以进行特征衍生增加适量的特征
• 简化模型，减少复杂度
• 还有贝叶斯法、多种模型结合等方法

在以后的文章中会尽量提到，今天就到此为止吧。