初学GAN（WGAN-gp)生成直线的小实验，以及一个可能很有用的小想法——加校正的WGAN-gp

一直以来对各种利用GAN来生成各种有趣的图像的应用很感兴趣，也想学习一下。前两天终于动手实践了一下，终于学会了GAN基本的方法。然后我又东改改西改改，又发现了两个很有趣的小方法，感觉挺实用的。我这个人看论文比较少，也许别人已经提出来过，但是我没有看到过。反正不管有没有人提出过，我都写下来吧。我这个人很懒，隔几年才写个博客，不过我写下来的，都是我觉得比较有趣的想法，这次这个我觉得还是挺有意思的，值得花点时间记下来。

GAN网络的基本知识我就不多说了，资料太多了，我也说不好，等会直接上代码。

先说说这两个想法:

一个是一次前向和反向把判别器D和生成器G同时都训练了，可以节省大于1/5的时间，以及少写几行代码^_^。

另一个则是由于生成的效果总是不让我很满意，然后我想出了一个办法，新增了一个我称之为“校正"(Correct)网络，然后用这个校正网络去校正一下生成器的输出，再用校正后的输出作为期望输出来计算一个校正损失作为损失的一部分。加入这个校正输出，以及其它的一些方法后，效果明显。具体方法后面再详说。

我用了最原始的GAN和据说很好的WGAN-gp两种方法来实现。我选的例子很简单，教生成器生成9个数的等差数列，画出来就是一条9个点的直线。之所以选这个例子，一是作为我的第一个GAN代码，以掌握方法为主，不想搞太复杂，二是一条直线，很容易观察生成质量的好坏，而如果是个很复杂的图形的话，一来需要的时间长，代码复杂，二来质量评估不是很直观。而直线的质量好不好，一眼就看出来了，很细微的弯曲都是很明显的。事实上，也正是由于直线的弯曲太显眼了，所以让我对WGAN-gp最后输出的结果还是不太满意（虽然比原始GAN好多了），然后才想了各种各样的方法，最后通过加上校正器C，才最终改善了质量，生成了笔直的直线。

先看看效果。我每个batch用400条直线。图例中的数字是这条直线被辨别器D打的分，越高越好。原始GAN是加了sigmoid的，分值是0到1，WGAN-gp分值是没有限制的，但由于梯度惩罚项的存在，数值也不会太大。

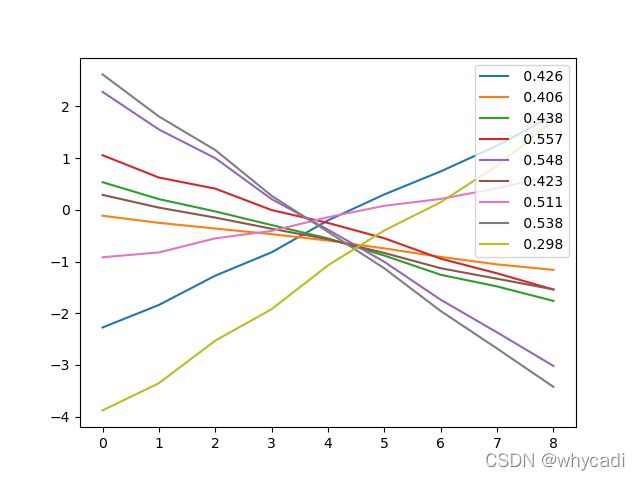
这是原始GAN网络训练40000次的效果，质量嘛……就不说了。

这是WGAN-gp训练10000次的效果，可以看出要好得多，但还是有些弯曲

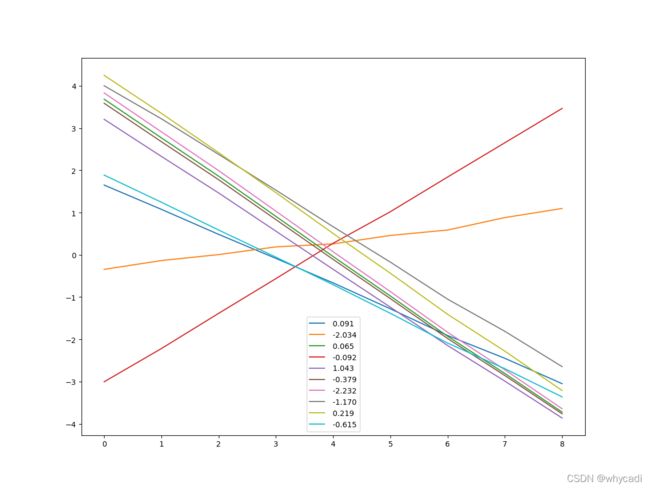
 这是WGAN-gp训练10000次，但采用了同时训练D和G的效果，可以看出效果与分别训练的差不多，但时间上可以节省大约1/4。

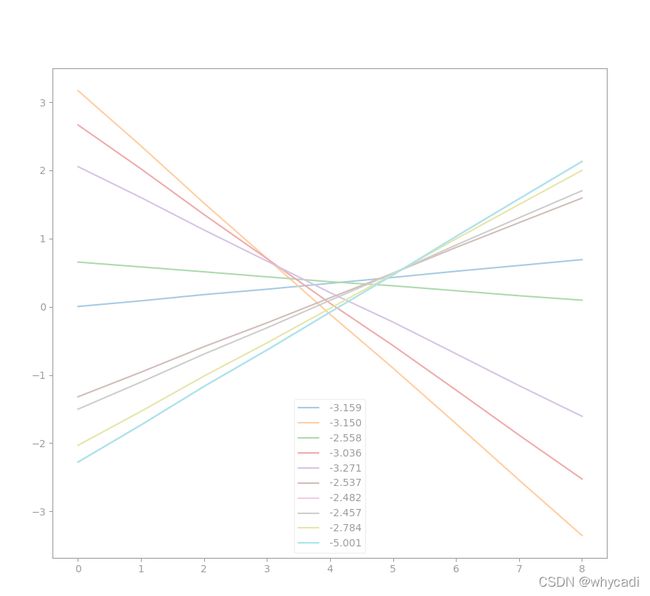
 好了，这是加了校正器C，训练5000次的效果。

 可以看出质量好太多了，训练次数少一半，肉眼就已经看不出明显的弯曲了。虽然由于要多训练一个校正器，总时间上与不加校正的差不多

 这是我觉得上面打分出来的数值的绝对值太大了，由于打分输出的均值就是loss，太大了感觉不太好，所以我在训练判别器时又加了个打分的二次均方惩罚项，这样输出的打分值的绝对值就小一些了。

 

首先说下同时训练判别器D和生成器G的方法。我照着网上的教程和代码写代码的时候，发现在训练判别器D时，先要用生成网络产生一些负样本，然后在计算判别器的loss时，要把这个负样本输入到判别器，然后backward一下，教程视频上老师这个时候还专门说明了这个时候要把这个负样本detach一下，避免反向计算梯度时计算生成器的梯度。然而呢，在后面训练生成器的时候，又要把这个过程做一遍，只是这个时候需要把梯度计算传递到生成器上，并且此时生成器需要的loss与判别器是反的。大致的过程是这个样子的：

1 用真实数据dataTrue给判别器D，得到输出outTrue

2 用随机数据给生成器，生成假数据dataFake , 并且把dataFake.detach()一下，再把dataFack给判别器D，得到outFake

3 计算D的lossD = -E[ log(outTrue] + E[ log (1-outFake)]

4 反向传递 lossD , 然后用优化器更新 判别器D

5 接下来要训练生成器G了，还是先用随机数据给生成器，生成假数据dataFake，这时不能detach了，然后把dataFack给判别器D，得到outFake

6 G的损失 lossG就是 -E[ log(1-outFake)]

7 反向传递lossG，然后用优化器更新生成器

这里我们发现，在训练D和G的时候，都要生成一个dataFake，然后输入给D产生一个outFake，然后loss中都有一个E[ log(1-outFake)]，只不过一个是负的，一个是正的，并且在训练D的时候，不需要把梯度计算到生成器G中，但是呢，如果不detach一下，实际上也是会计算下去的，这个计算时间就浪费了，所以视频上才强调要detach一下。

可是我却发现是不是可以反其道而行之，干脆一次把训练生成器G的梯度也算了，反正只差一个负号，把lossD反向完了以后，把存在G网络参数里的梯度取个反就行了。实现代码也就几行

        #直接把生成器的梯度取反进行训练，可节省一次正向推演
        for name,para in gNet.named_parameters():
            if '.weight' in name or '.bias' in name:
                para.grad*=-1
        optimG.step()

抱着试试看的想法试了一下，发现生成器G还真的能更新，效果和单独训练差不多，而时间上节省了大约1/5，简直是白赚。特别是还能少写几行代码。

接下来先上原始GAN的代码。里面为了在线显示效果，加了个画图线程，每1000个batch从生成的直线中抽前10条出来显示。

import numpy as np
import torch
import torch.nn as nn
import os
import matplotlib
import matplotlib.pyplot as plt
import threading as thread
import time

'''测试GAN对抗生成网络
生成一个中项±1之间 ，项差±1之间的 n个数的等差数列 ，即构成一条直线 '''

savePathD='GAN_Dnet.pkl'
savePathG='GAN_Gnet.pkl'
pNum=9  #9个点
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

#判断网络
class DNet(nn.Module):
    def __init__(self):
        super(DNet,self).__init__()
        self.fc1=nn.Linear(pNum,64)
        self.fc2=nn.Linear(64,64)
        self.fout=nn.Linear(64,1)
    def forward(self,input):
        out=self.fc1(input.view(-1,pNum))
        out=torch.tanh(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fout(out)

        return torch.sigmoid(out)

#生成网络
class GNet(nn.Module):
    def __init__(self):
        super(GNet,self).__init__()
        self.fc1=nn.Linear(1,16)
        self.fc2=nn.Linear(16,64)
        self.fc3=nn.Linear(64,32)
        self.fout=nn.Linear(32,pNum)
    def forward(self,input):
        out=self.fc1(input.view(-1,1))
        out=torch.celu(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fc3(out)
        out=torch.celu(out)
        out=self.fout(out)
        return out

#生成数据函数
def CreateData(num,pointnum):
    mu=np.random.random([num,1])*2-1
    delta=np.random.random([num,1])*2-1
    diffs=[i-(pointnum//2) for i in range(pointnum)]
    data=mu+diffs*delta
    return torch.tensor(data,dtype=torch.float)

#显示线程
record=[]       #生成的部分供显示数据
score=[]
refresh=False
finish=False
def displayThread(lock):
    global record,score,refresh
    fig,ax=plt.subplots()
    x=[i for i in range(pNum)]
    while not finish:
        if refresh:
            lock.acquire()
            recs=record[:]
            sco=score[:]
            refresh=False
            lock.release()

            for idx in range(len(record)):
                plt.plot(x,recs[idx],label=' %5.3f'%sco[idx])
            plt.legend()
            plt.pause(2)
            ax.cla()
        else:
            time.sleep(2)
dlock=thread.RLock()
dthread=thread.Thread(target=displayThread,args=(dlock,))
dthread.start()


dNet=DNet().to(device)
gNet=GNet().to(device)

if os.path.exists(savePathD):
    dNet.load_state_dict(torch.load(savePathD))
if os.path.exists(savePathG):
    gNet.load_state_dict(torch.load(savePathG))

optimD=torch.optim.Adam(dNet.parameters(),lr=5e-4,betas=(0.5,0.9))
optimG=torch.optim.Adam(gNet.parameters(),lr=5e-4,betas=(0.5,0.9))

epoch=10000
batch=400
'''for name, para in gNet.named_parameters():
    if '.weight' in name or '.bias' in name:
        print(name)'''
start=time.time()
for ep in range(epoch):
    #训练判别器
    for _ in range(2):
        optimD.zero_grad()
        optimG.zero_grad()
        #生成真数据
        dataT=CreateData(batch,pNum).detach().to(device)
        pR=dNet(dataT)
        lossR = -pR.log().mean()
        #使用生成网络生成假数据
        #如果判断器和生成器分别训练，这里加上no_grad可节省内存和时间，如果要用到后面的同时训练方法此必须保留梯度
        #with torch.no_grad():
        gInput=(torch.rand([batch,1])*2-1).to(device)
        dataF=gNet(gInput)#.detach()
        pF = dNet(dataF)
        lossF=(1-pF).log().mean()
        lossD=lossR-lossF
        lossD.backward()
        optimD.step()
        #直接把生成器的梯度取反进行训练，可节省一次正向推演
        for name,para in gNet.named_parameters():
            if '.weight' in name or '.bias' in name:
                para.grad*=-1
        optimG.step()
    ''' 
    #训练生成器
    for _ in range(2):
        optimD.zero_grad()
        optimG.zero_grad()
        gInput=(torch.rand([batch,1])*2-1).to(device)
        dataF=gNet(gInput)
        pGF=dNet(dataF)
        lossG=(1-pGF).log().mean()
        lossG.backward()
        optimG.step()'''
    #打印看看结果
    if (ep+1)%200==0:
        now=time.time()
        print(ep+1,round(now-start,4),'Loss R=',pR.mean().item(),' ,loss F=',pF.mean().item())
        start=now
        dlock.acquire()
        record=dataF[:10].to('cpu').tolist()
        score=pF[:10].to('cpu').view(-1).tolist()
        refresh=True
        dlock.release()
        #print('      G Point=',pGF.mean().item(),' bast point is ',pF.max().item())
    if (ep+1)%1000==0:
        torch.save(dNet.state_dict(),savePathD)
        torch.save(gNet.state_dict(),savePathG)
input("press enter to exit")
finish=True
dthread.join()

一共就150行左右。其中开始单独训练生成器那段代码后来用了同时训练的技巧后就用''' '''长字符串符给注释掉了。

接下来就是WGAN-gp了。WGAN-gp相比于原始GAN，改动主要是这么几点：

1 判别器D的最后输出去掉了sigmoid

2 训练判别器的优化器，一定不能带动量，也就是常用的Adam不能用了，实际中试了试别的，发现还就只有推荐的RMSprop能用。

3 加入了一个梯度惩罚项。主要实现是这么一段代码

#梯度惩罚计算
def grad_penalty(D,xr,xf):
    rate = torch.rand([len(xr), 1]).to(device)
    mid=rate*xr+(1-rate)*(xf.detach())
    mid.requires_grad_()
    pred=D(mid)
    grads=torch.autograd.grad(outputs=pred,inputs=mid,grad_outputs=torch.ones_like(pred),
                              create_graph=True,retain_graph=True,only_inputs=True)[0]
    gp=torch.pow(grads.norm(2,dim=1)-1,2).mean()
    return gp

以及在算判别器ossD时加上这一项

        lossgp=grad_penalty(dNet,dataT,dataF)
        lossD=lossR+lossF+0.2*lossgp

这段代码我自己是写不出来的，从网上抄的。当然抄了以后大概明白是什么意思了。这个代码先是以一定的概率比例混合了真数据和假数据，形成一个混合输入mid，然后把这个mid给判别器得到输出pred，然后将pred对输入求导，反向传输到输入端，得到梯度grads,再强制要求这个grads里的值都应该向±1靠拢。这就是WGAN-gp论文里的那个gp项。只是光看论文我是不知道该怎么实现的。

这里用到了pytorch的自动求导机制里的一些特别参数，主要是retain_graph这个参数。pytorch要正确的求导，其实内部是需要保存整个计数图的结构和参数的，这是很占空间的，往往显存不够用就是因为中间数据需要保存，占用了大量的空间。那么pytorch默认你backward了以后，这些数据就不再需要了，于是就把这些数据都删掉了，此时如果你再求一次导，这样就会报错，因为求导所需的数据已经没了。但如果你真的需要再求一次导呢？比如这里你算完了梯度惩罚项，还需要利用计算图再求这个惩罚项对梯度的影响，那么就必须告诉pytorch先不要删这些数据,要留着下次还有用。这样在下次lossD的backward时才不会报错。

整个代码如下：

import numpy as np
import torch
import torch.nn as nn
import os
import matplotlib
import matplotlib.pyplot as plt
import threading as thread
import time

'''测试WGAN-gp对抗生成网络
效果比原始GAN要好很多
并且使用同时训练G,D的方法，节省了约20%的时间，效果似乎还略好
生成一个中项±1之间 ，项差±1之间的 n个数的等差数列 ，即构成一条直线 '''

savePathD='WGANgp_Dnet.pkl'
savePathG='WGANgp_Gnet.pkl'
pNum=9  #9个点
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

#判断网络
class DNet(nn.Module):
    def __init__(self):
        super(DNet,self).__init__()
        self.fc1=nn.Linear(pNum,64)
        self.fc2=nn.Linear(64,64)
        self.fout=nn.Linear(64,1)
    def forward(self,input):
        out=self.fc1(input.view(-1,pNum))
        out=torch.tanh(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fout(out)
        return out  #wgan 不进行sigmoid

#生成网络
class GNet(nn.Module):
    def __init__(self):
        super(GNet,self).__init__()
        self.fc1=nn.Linear(1,16)
        self.fc2=nn.Linear(16,64)
        self.fc3=nn.Linear(64,32)
        self.fout=nn.Linear(32,pNum)
    def forward(self,input):
        out=self.fc1(input.view(-1,1))
        out=torch.celu(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fc3(out)
        out=torch.celu(out)
        out=self.fout(out)
        return out

#生成数据函数
def CreateData(num,pointnum):
    mu=np.random.random([num,1])*2-1
    delta=np.random.random([num,1])*2-1
    diffs=[i-(pointnum//2) for i in range(pointnum)]
    data=mu+diffs*delta
    return torch.tensor(data,dtype=torch.float)

#显示线程
record=[]       #生成的部分供显示数据
score=[]
refresh=False
finish=False
def displayThread(lock):
    global record,score,refresh
    fig,ax=plt.subplots()
    x=[i for i in range(pNum)]
    while not finish:
        if refresh:
            lock.acquire()
            recs=record[:]
            sco=score[:]
            refresh=False
            lock.release()

            for idx in range(len(record)):
                plt.plot(x,recs[idx],label=' %5.3f'%sco[idx])
            plt.legend()
            plt.pause(2)
            ax.cla()
        else:
            time.sleep(2)
dlock=thread.RLock()
dthread=thread.Thread(target=displayThread,args=(dlock,))
dthread.start()


dNet=DNet().to(device)
gNet=GNet().to(device)

if os.path.exists(savePathD):
    dNet.load_state_dict(torch.load(savePathD))
if os.path.exists(savePathG):
    gNet.load_state_dict(torch.load(savePathG))

optimD=torch.optim.RMSprop(dNet.parameters(),weight_decay=0.01)
optimG=torch.optim.Adam(gNet.parameters(),weight_decay=0.01,lr=5e-4,betas=(0.5,0.9))

#梯度惩罚计算
def grad_penalty(D,xr,xf):
    rate = torch.rand([len(xr), 1]).to(device)
    mid=rate*xr+(1-rate)*(xf.detach())
    mid.requires_grad_()
    pred=D(mid)
    grads=torch.autograd.grad(outputs=pred,inputs=mid,grad_outputs=torch.ones_like(pred),
                              create_graph=True,retain_graph=True,only_inputs=True)[0]
    gp=torch.pow(grads.norm(2,dim=1)-1,2).mean()
    return gp



epoch=5000
batch=400
'''for name, para in gNet.named_parameters():
    if '.weight' in name or '.bias' in name:
        print(name)'''
start=time.time()
for ep in range(epoch):
    #训练判别器
    for _ in range(2):
        optimD.zero_grad()
        optimG.zero_grad()
        #生成真数据
        dataT=CreateData(batch,pNum).detach().to(device)
        pR=dNet(dataT)
        lossR = -pR.mean()
        #使用生成网络生成假数据
        #如果判断器和生成器分别训练，这里加上no_grad可节省内存和时间，如果要用到后面的同时训练方法此必须保留梯度
        #with torch.no_grad():
        gInput=(torch.rand([batch,1])*2-1).to(device)
        dataF=gNet(gInput)#.detach()
        pF = dNet(dataF)
        lossF=pF.mean()
        #输出值过大惩罚
        #lossV=torch.pow(pF+1, 2).mean()+torch.pow(pR-1,2).mean()
        lossgp=grad_penalty(dNet,dataT,dataF)
        lossD=lossR+lossF+0.2*lossgp#+0.01*lossV  #一旦加上输出过大惩罚，就不能合并G和D训练了
        lossD.backward()
        optimD.step()
        #直接把生成器的梯度取反进行训练，可节省一次正向推演
        for name,para in gNet.named_parameters():
            if '.weight' in name or '.bias' in name:
                para.grad*=-1
        optimG.step()
    ''' 
    #训练生成器
    for _ in range(2):
        optimD.zero_grad()
        optimG.zero_grad()
        gInput=(torch.rand([batch,1])*2-1).to(device)
        dataF=gNet(gInput)
        pGF=dNet(dataF)
        lossG=-pGF.mean()
        lossG.backward()
        optimG.step()'''
    #打印看看结果
    if (ep+1)%200==0:
        now=time.time()
        print(ep+1,round(now-start,4),'Loss R=',pR.mean().item(),' ,loss F=',pF.mean().item())
        start=now
        dlock.acquire()
        record=dataF[:10].to('cpu').tolist()
        score=pF[:10].to('cpu').view(-1).tolist()
        refresh=True
        dlock.release()
        #print('      G Point=',pGF.mean().item(),' bast point is ',pF.max().item())
    if (ep+1)%1000==0:
        torch.save(dNet.state_dict(),savePathD)
        torch.save(gNet.state_dict(),savePathG)
input("press enter to exit")
finish=True
dthread.join()

WGAN-gp果然名不虚传，效果比原始GAN要好很多，如果生成的不是直线而是个什么图像之类的话，对于一个没有什么美术鉴赏细胞的人，说不定我就心满意足的结束这第一次的GAN学习了。然而我选材不善，偏偏选了个最容易看出细微差距的东西，那就是直线。直线这个东西，真是哪怕只有一点点弯曲都是那么明显，让我这个中度强迫症患者无法释怀。

在经过了一大堆各种参数调整未果以后，我最终觉得还是得从哲学感觉上想想了。

这个GAN网络，就好像一个学画画的学生，和一个很不友善的老师，学生画了一幅画，拿给老师去看，老师只会说“这画的什么垃圾！”，“不要让我再看到这种东西！”，“你就不是画画的料”，“别人画画是要钱，你画画是要命啊！”……，总之，得到的永远就是各种不好，最多也就是“不好”和“很不好”以及“非常不好”的区别，但是哪不好了，该怎么改，老师就是不说。这个悲惨的学生只能永远在负向反馈中寻找前进的方向。显然这种完全没有正向引导的学习是痛苦的，如果现实中摊上这么个老师，恐怕最后只能流血五步了。更过分的是，即使学生终于摸索出一条正确的道路，接近了好的境界，这时这个老师反而不能给出很好的评价了，因为这个老师已经分不清好坏了，给出的评价的参考价值大大降低。这也可能就是为什么最后的直线总是有一点点弯，因为这个时候很难从评价中得到有效的指导。

如果此是你有一个师兄，他能够每次给你一些改进意见，在你的画上修改几笔，使之变得更好一些，那么对你的学习效率的提高无疑是有巨大帮助的，即使这个师兄每次只能给你很少的一些改进，甚至改进意见不那么靠谱也没关系。

那么怎么样让这个师兄能够从你的画上得到一个比较靠谱的改进意见呢？我想到了几种假设，其中对于画直线这个应用比较简单的是这个方法：再创建一个校正网络C（orrectNet），取真实数据即很好的直线，叠加一部分生成数据作为噪声，然后让这个校正网络C学习如果从叠加了噪声的数据中尽可能的恢复无噪声数据，即让这个校正网络起到一个滤波器的作用，或者说，能够最大保留真实数据的分布，尽可能从中去除生成数据中与真实数据分布差异较大的部分的数据。然后，我们用这个校正网络来对生成数据进行校正，使之能够更接近真实数据，最后以生成网络的原始数据与校正过的数据的误差作为校正loss，作为lossG的一部分。

考虑到前期校正网络不那么可靠，而后期判别网络的评价质量下降，我让这两部分loss的比例随着训练的进行而改变，前期判别网络损失比例大，后期校正网络损失比例大，但判别网络损失比例不能太小，否则可能出现模式塌陷的现象。

校正器的训练放在生成器训练之前。由于生成器的loss叠加了校正器的误差，再也不太好与判别器的误差反向传输合并了（其实还是可以的，有点麻烦，而且节省的时间比例也不大了），所以这里生成器的训练就不与判别器合并了。整个代码如下

import numpy as np
import torch
import torch.nn as nn
import os
import matplotlib
import matplotlib.pyplot as plt
import threading as thread
import time

'''测试WGAN对抗生成网络
生成一个中项±1之间 ，项差±1之间的 n个数的等差数列 ，即构成一条直线 
尝试不使用gp惩罚，只截断loss计算时判断器的输出,效果比gp差远了
加入校正网络,效果明显改善
加入对判别器输出的幅值惩罚，似乎也有一定改善
生成器训练中。对于判断器传回的loss，比重逐渐减小，因为判断器输出的质量是不断降低的'''

savePathD='WGANc_Dnet.pkl'
savePathG='WGANc_Gnet.pkl'
pNum=9  #9个点
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

#判断网络
class DNet(nn.Module):
    def __init__(self):
        super(DNet,self).__init__()
        self.fc1=nn.Linear(pNum,64)
        self.fc2=nn.Linear(64,64)
        self.fout=nn.Linear(64,1)
    def forward(self,input):
        out=self.fc1(input.view(-1,pNum))
        out=torch.tanh(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fout(out)

        return out  #wgan 不进行sigmoid

#生成网络
class GNet(nn.Module):
    def __init__(self):
        super(GNet,self).__init__()
        self.fc1=nn.Linear(1,16)
        self.fc2=nn.Linear(16,64)
        self.fc3=nn.Linear(64,32)
        self.fout=nn.Linear(32,pNum)
    def forward(self,input):
        out=self.fc1(input.view(-1,1))
        out=torch.celu(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fc3(out)
        out=torch.celu(out)
        out=self.fout(out)
        return out

#校正网络
class CNet(nn.Module):
    def __init__(self):
        super(CNet,self).__init__()
        self.fc1=nn.Linear(pNum,64)
        self.fc2=nn.Linear(64,128)
        self.fc3=nn.Linear(128,64)
        self.fout=nn.Linear(64,pNum)
    def forward(self,input):
        out=self.fc1(input.view(-1,pNum))
        out=torch.celu(out)
        out=self.fc2(out)
        out=torch.celu(out)
        out=self.fc3(out)
        out=torch.celu(out)
        out=self.fout(out)
        return out
cNet=CNet().to(device)
optimC=torch.optim.Adam(cNet.parameters())
lossCfun=torch.nn.MSELoss()
#校正损失函数
def correct_loss(C,xr,xf):
    rate = (0.1*torch.rand([len(xr), 1])).to(device)
    mid=(1-rate)*xr+rate*(xf.detach())
    #训练一次校正网络
    out1=C(mid)
    lossC=lossCfun(xr,out1)
    optimC.zero_grad()
    lossC.backward()
    optimC.step()

    out2=C(xf)
    lossC=lossCfun(out2,xf)
    return lossC




#生成数据函数
def CreateData(num,pointnum):
    mu=np.random.random([num,1])*2-1
    delta=np.random.random([num,1])*2-1
    diffs=[i-(pointnum//2) for i in range(pointnum)]
    data=mu+diffs*delta
    return torch.tensor(data,dtype=torch.float)

#显示线程
record=[]       #生成的部分供显示数据
score=[]
refresh=False
finish=False
def displayThread(lock):
    global record,score,refresh
    fig,ax=plt.subplots()
    x=[i for i in range(pNum)]
    while not finish:
        if refresh:
            lock.acquire()
            recs=record[:]
            sco=score[:]
            refresh=False
            lock.release()

            for idx in range(len(record)):
                plt.plot(x,recs[idx],label=' %5.3f'%sco[idx])
            plt.legend()
            plt.pause(2)
            ax.cla()
        else:
            time.sleep(2)
dlock=thread.RLock()
dthread=thread.Thread(target=displayThread,args=(dlock,))
dthread.start()


dNet=DNet().to(device)
gNet=GNet().to(device)

if os.path.exists(savePathD):
    dNet.load_state_dict(torch.load(savePathD))
if os.path.exists(savePathG):
    gNet.load_state_dict(torch.load(savePathG))

optimD=torch.optim.RMSprop(dNet.parameters(),weight_decay=0.01)
optimG=torch.optim.Adam(gNet.parameters(),weight_decay=0.01,lr=5e-4,betas=(0.5,0.9))


#梯度惩罚计算
def grad_penalty(D,xr,xf):
    rate = torch.rand([len(xr), 1]).to(device)
    #rate=rate.expand_as(xr)
    #nrate=1-rate
    #print(rate.shape,nrate.shape,xr.shape,xf.shape)
    mid=rate*xr+(1-rate)*(xf.detach())
    mid.requires_grad_()
    pred=D(mid)
    grads=torch.autograd.grad(outputs=pred,inputs=mid,grad_outputs=torch.ones_like(pred),
                              create_graph=True,retain_graph=True,only_inputs=True)[0]
    gp=torch.pow(grads.norm(2,dim=1)-1,2).mean()
    return gp


epoch=5000
batch=400
'''for name, para in gNet.named_parameters():
    if '.weight' in name or '.bias' in name:
        print(name)'''
start=time.time()
for ep in range(epoch):
    #训练判别器
    for _ in range(2):
        optimD.zero_grad()
        optimG.zero_grad()
        #生成真数据
        dataT=CreateData(batch,pNum).detach().to(device)
        pR=dNet(dataT)
        #lossR= -torch.clamp_max(pR,1.).mean()
        lossR = -pR.mean()
        #使用生成网络生成假数据
        #如果判断器和生成器分别训练，这里加上no_grad可节省内存和时间，如果要用到后面的同时训练方法此必须保留梯度
        #如果要加入校正网络，则还是分别训练比较好
        with torch.no_grad():
            gInput=(torch.rand([batch,1])*2-1).to(device)
            dataF=gNet(gInput)#.detach()
        pF = dNet(dataF)
        #lossF=torch.clamp_min(pF,-1.).mean()
        lossF=pF.mean()
        #梯度惩罚
        lossgp=grad_penalty(dNet,dataT,dataF)
        #输出值过大惩罚
        lossV=torch.pow(pF+1, 2).mean()+torch.pow(pR-1,2).mean()

        lossD=lossR+lossF+0.2*lossgp+0.02*lossV
        lossD.backward()
        optimD.step()

        #训练校正器
        rate = (0.1 * torch.rand([len(dataT), 1])).to(device)
        mid = (1 - rate) * dataT + rate * (dataF-dataF.mean(-1).view(-1,1)).detach()
        # 训练一次校正网络
        out1 = cNet(mid)
        lossC = lossCfun(dataT, out1)
        optimC.zero_grad()
        lossC.backward()
        optimC.step()
        '''
        #直接把生成器的梯度取反进行训练，可节省一次正向推演
        for name,para in gNet.named_parameters():
            if '.weight' in name or '.bias' in name:
                para.grad*=-1
        optimG.step()
    ''' 
    #训练生成器
    for _ in range(1):
        optimD.zero_grad()
        optimG.zero_grad()
        gInput=(torch.rand([batch,1])*2-1).to(device)
        #生成假数据并通过判断网络
        dataF=gNet(gInput)
        pGF=dNet(dataF)
        #将假数据通过校正网络得到校正数据和校正误差
        dataC=cNet(dataF.detach())
        lossC=lossCfun(dataC,dataF)
        #总误为
        lossG=(max(0.1,0.99**(ep//10)))* -pGF.mean()+0.2*lossC
        lossG.backward()
        optimG.step()
    #打印看看结果
    if (ep+1)%200==0:
        now=time.time()
        print(ep+1,round(now-start,4),'Loss R=',pR.mean().item(),' ,loss F=',pF.mean().item())
        start=now
        dlock.acquire()
        record=dataF[:10].to('cpu').tolist()
        score=pF[:10].to('cpu').view(-1).tolist()
        refresh=True
        dlock.release()
        #print('      G Point=',pGF.mean().item(),' bast point is ',pF.max().item())
    if (ep+1)%1000==0:
        torch.save(dNet.state_dict(),savePathD)
        torch.save(gNet.state_dict(),savePathG)
input("press enter to exit")
finish=True
dthread.join()

加入校正器后的效果是明显的，只用了一半的训练次数就得到了笔直的直线，几乎没有肉眼可觉的曲折。

事后再深入的想一下，值得庆幸的是，直线这个应用中，真实数据（好的直线）和生成数据，它们的空间是有很大重合的。通过直接比例混合的方法就可以得到比较好的混合样本，在这个样本上训练的校正器作用到生成数据上能够得到改进的效果的可能性是比较大的。而如果更高维和复杂的空间，这种简单混合的方法是否能得到这么好的效果呢？或者真实样本的质量就不太好，本身就混杂了很多噪声的情况下，又会怎么样呢？

从这几个方面，我想了一些可以产生比较好的校正器训练样本的方法。除了混合以外，似乎还可以利用判别器的输出信息来作为样本质量的依据。我们基于以下的假设：

1 可以认为WGAN中判别器D的输出是一个样本质量的评估

2 同一个噪声通过代际相隔不远的生成器G生成的样本，它们之间的差异是不大的

基于这样两个假设，我们可以保留上代或几代的输入噪声以及对应的生成样本数据，然后在每一代训练中，从这些历史输入中挑选一些，生成新的样本，然后把两代生成的样本输入到判别器中，得到它们的评分，然后以这两个样本中得分低的作为校正器的输入，得分高的作为校正器的期望输出。通过这种样本，以及通过对真实样本叠加噪声的样本这两种样本来训练校正器，从而得到一个能够比较好的对生成器输出进行改进的校正器。

实际上，我们甚至可以直接把这两代样本的差作为生成器的输出的训练的一部分loss，如果上代的评分比这代高，那么就引导本代输出向上代靠拢（比如MSELoss)，反之，则更加远离(MSELoss取个反）。

另外，也可以从校正器上动些手脚。校正器实际上可以拆开为一个自编码器和一个解码器。我们可以对真实样本的编码进行聚类，然后对生成样本的编码进行改变，使之向就近的真实样本编码聚类中心靠拢一部分，然后解码之，再通过判别网络进行评判，如果评分提高，则将这个输出作为一个更好的输出并引导生成网络去学习。

还有其它的一些想法，先写这么多吧。以后有机会慢慢试试效果。本次第一次的GAN网络实现算是取得了不错的效果。不过我这个人兴趣广泛但是转移太快，工作上又没机会专一深入研究某一课题，怕以后没有机会再深入了。