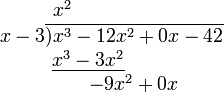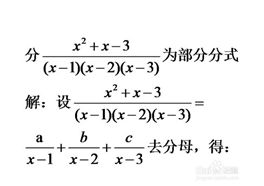-
多项式长除法
简介
多项式长除法 是代数中的一种算法,用一个同次或低次的多项式去除另一个多项式。是常见算数技巧长除法的一个推广版本。它可以很容易地手算,因为它将一个相对复杂的除法问题分解成更小的一些问题。
示例
计算
-
把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐,写成以下这种形式:
-
然后商和余数可以这样计算:
将分子的第一项除以分母的最高次项(即次数最高的项,此处为x)。结果写在横线之上(x3 ÷ x = x2).
-
将分母乘以刚得到结果(最终商的第一项),乘积写在分子前两项之下(同类项对齐) (x2 · (x − 3) = x3 − 3x2).
-
从分子的相应项中减去刚得到的乘积(消去相等项,把不相等的项结合起来),结果写在下面。((x3 − 12x2) − (x3 − 3x2) = −12x2 + 3x2 = −9x2)然后,将分子的下一项"拿下来"。
-
把减得的差当作新的被除式,重复前三步(直到余式为零或余式的次数低于除式的次数时为止.被除式=除式×商式+余式 )
-
重复第四步。这次没什么可以"拿下来"了。
-
横线之上的多项式即为商,而剩下的 (−123) 就是余数。
除法变换
使用多项式长除法可以将一个多项式写成 除数-商 的形式(经常很有用)。 考虑多项式 P(x), D(x) ((D)的次数 < (P)的次数)。 然后,对某个商多项式 Q(x) 和余数多项式R(x) ((R)的系数 < (D)的系数),
这种变换叫做除法变换,是从算数等式 .[1] 得到的。
原文地址:http://zh.wikipedia.org/wiki/%E5%A4%9A%E9%A1%B9%E5%BC%8F%E9%95%BF%E9%99%A4%E6%B3%95
- 部分分式展开法
当分母为一个高次幂的单项式时。
我们可以先设定幂数由低到高的次序的系数,如图中所示。
将分式去掉分母后之后,根据两个多项式是相等的多项式的原理,列出系数a、b、c的方程组。
解方程组,得出系数a、b、c的值,代入之前列出的带有系数的多项式即可。
那么当分母是多个一次幂的单项式时,我们可以把每个单项式作为一个分母列出,然后分子设定为选定的系数。
去掉分母后,用假设法先根据分母中单项式来假设x的值(就是分别能使单项式等于零的值)来求解系数a、b、c的值。
将求得的系数代入即可得出最后结果。
还可使用综合除法,步骤如下
部分节选自网络