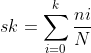常用图像增强算法实现——直方图均衡

1.前言

对于原始对比度较低的图像，我们可以提高对比度来增强图像的辨识度，改善图像的视觉效果，转换为更适合人或者机器处理的形式，去除无用的信息，提高使用价值。典型的比如CT图像增强，去雾去雨，静脉增强等算法。

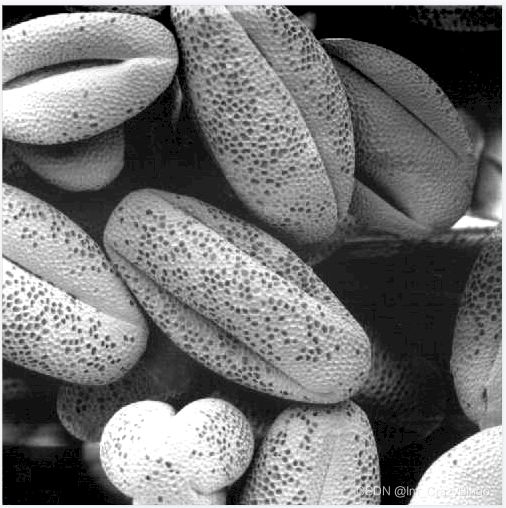
从人眼视觉特性来考虑，一幅图像的灰度直方图如果是均匀分布的，那么该图像看上去效果比较好（理论上）；当然如果需要进一步进行图像分类或者机器学习，图像的预处理增强，也有助于目标的识别与检索。如下图所示，为《数字图像处理Matlab版》（冈萨雷斯）一书中，关于图像增强（直方图均衡的例子），直观可见，左图对比度低，图像朦胧看着很不自然，右图就很适合人眼的视觉特性，对比度、辨识度甚至舒适度都有很大的提升。

  那么，本章，我们就主要讲讲几种基本的图像增强算法的Matlab & FPGA实现。常用的图像增强算法，广义的讲不仅包括对比度、直方图等，降噪滤波、锐度饱和度等也属于ISP领域的图像增强。但本章主要讲针对直方图均衡，和各种对比度算法的图像增强，其他内容将在后续章节中，再进一步展开介绍。

2.直方图均衡原理

直方图均衡也称直方图拉伸，是一种简单有效的图像增强技术，通过改变图像的直方图分布，来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰（如上图左），曝光不足将使图像灰度级集中在低亮度范围内。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。

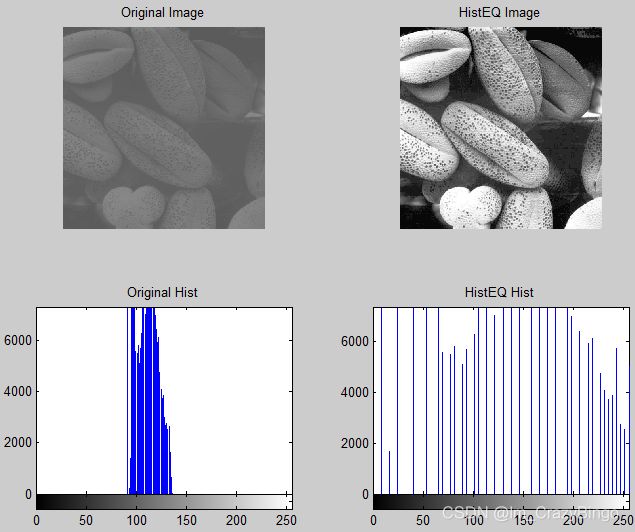
换言之，直方图均衡化的基本原理是：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。以上述图片为例，均衡化之前的直方图，及均衡化后的直方图，如下所示：

 

% -----------------------------------------------------------------------
% 								 \\\|///
% 							   \\  - -  //
% 								(  @ @  )
% +---------------------------oOOo-(_)-oOOo-----------------------------+
% CONFIDENTIAL IN CONFIDENCE
% This confidential and proprietary software may be only used as authorized
% by a licensing agreement from CrazyBingo (Thereturnofbingo).
% In the event of publication, the following notice is applicable:
% Copyright (C) 2013-20xx CrazyBingo Corporation
% The entire notice above must be reproduced on all authorized copies.
% Author				:		CrazyBingo
% Technology blogs 	    : 		www.crazyfpga.com
% Email Address 		: 		[email protected]
% Filename			    :		Image_HistEQ1.m
% Date				    :		2021-08-25
% Description			:		Histgram EQ for gray image
% Modification History	:
% Date			By			Version			Change Description
% =========================================================================
% 21/08/25		CrazyBingo	1.0				Original
% -------------------------------------------------------------------------
% |                                    Oooo							  |
% +-----------------------------oooO--(   )-------------------------------+
%                              (   )   ) /
%                               \ (   (_/
%                                \_)
% -----------------------------------------------------------------------


clear all;  %清除Matlab缓存数据
close all;
clc;

% -------------------------------------------------------------------------
% Read PC image to Matlab
IMG1 = imread('../images/test1.tif');    % 读取jpg图像
h = size(IMG1,1);         % 读取图像高度
w = size(IMG1,2);         % 读取图像宽度

% -------------------------------------------------------------------------
% IMG2 = rgb2gray(IMG1);    % 转灰度图像 
subplot(221), imshow(IMG1); title('Original Image');
subplot(223), imhist(IMG1); title('Original Hist');

IMG2 = zeros(h,w); 
IMG2 = histeq(IMG1);      % Matlab自带直方图均衡
subplot(222), imshow(IMG2); title('HistEQ Image');
subplot(224), imhist(IMG2); title('HistEQ Hist');

图像的灰度值是一个线性函数，但像素的分布（灰度直方图）是一个一维的离散函数，重点是直方图如何分布。 如上图中直方图分布可见，左图像素值基本上都聚集在100-130之间，而在直方图均衡化之后，像素值则均匀的分布在0-255之间。实际在直方图均衡化后的图，也有更高的对比度，自然更高的清晰度与辨识度。

图像f(x,y)灰度直方图的一维离散函数，可表示如下(L-1一般为255)：

h(k) = n(k)        k=0,1,...,L-1

其中n(k)为图像f(x,y)中灰度级为k的像素个数，对应直方图坐标中对于x轴的y列。图像的视觉效果与直方图有直接的对应关系，改变直方图的分布，对图像的结果也有很大的影响。我们进一步计算灰度级数出现的频率Pr(k)，如下(其中N为图像的像素数量)：

Pr(k) = n(k)/N

接着，计算原始图像灰度累计分布频率，即：

最后，采用累计分布频率，通过对结果扩大到L-1倍，得到最终均衡化后的图像，计算如下：

sk=sk*(L-1)

3.直方图均衡Matlab实现

如上整理流程，基本思路就是计算归一化后灰度级数频率的累计值，再将结果拉伸到0-255，因此直方图均衡，也叫做直方图拉伸。笔者并没有用复杂的公式去推导，简单地说直方图均衡的原理就是将直方图拉伸到0-255，因此根据累计的频率扩大255倍就可以得到理论的结果。接下来笔者将采用Matlab源代码方式实现直方图均衡，代码如下：

% -----------------------------------------------------------------------
% 								 \\\|///
% 							   \\  - -  //
% 								(  @ @  )
% +---------------------------oOOo-(_)-oOOo-----------------------------+
% CONFIDENTIAL IN CONFIDENCE
% This confidential and proprietary software may be only used as authorized
% by a licensing agreement from CrazyBingo (Thereturnofbingo).
% In the event of publication, the following notice is applicable:
% Copyright (C) 2013-20xx CrazyBingo Corporation
% The entire notice above must be reproduced on all authorized copies.
% Author				:		CrazyBingo
% Technology blogs 	    : 		www.crazyfpga.com
% Email Address 		: 		[email protected]
% Filename			    :		Image_HistEQ2.m
% Date				    :		2021-08-25
% Description			:		Histgram EQ for gray image
% Modification History	:
% Date			By			Version			Change Description
% =========================================================================
% 21/08/25		CrazyBingo	1.0				Original
% -------------------------------------------------------------------------
% |                                    Oooo							  |
% +-----------------------------oooO--(   )-------------------------------+
%                              (   )   ) /
%                               \ (   (_/
%                                \_)
% -----------------------------------------------------------------------


clear all;  
close all;
clc;

% -------------------------------------------------------------------------
% Read PC image to Matlab
IMG1 = imread('../images/test1.tif');    % 读取jpg图像
h = size(IMG1,1);         % 读取图像高度
w = size(IMG1,2);         % 读取图像宽度

% ----------------------------------------------
% Step1: 进行像素灰度级数统计
NumPixel = zeros(1,256);    %统计0-255灰度级数
for i = 1:h      
    for j = 1: w      
        NumPixel(IMG1(i,j) + 1) = NumPixel(IMG1(i,j) + 1) + 1;
    end      
end      

% Step2: 进行像素灰度级数累积统计    
CumPixel = zeros(1,256);      
for i = 1:256      
    if i == 1      
        CumPixel(i) = NumPixel(i);      
    else      
        CumPixel(i) = CumPixel(i-1) + NumPixel(i);      
    end      
end      
    
% Step3: 对灰度值进行映射（均衡化） = 归一化 + 扩大到255
IMG2 = zeros(h,w); 
for i = 1:h      
    for j = 1: w      
        IMG2(i,j) = CumPixel(IMG1(i,j)+1)/(h*w)*255;    
%        IMG2(i,j) = bitshift(CumPixel(IMG1(i,j)+1),-10);    
    end      
end      
IMG2 = uint8(IMG2);


% -------------------------------------------------------------------------
% IMG2 = rgb2gray(IMG1);    % 转灰度图像 
% figure;
subplot(231), imshow(IMG1);  title('Original Image');
subplot(234), imhist(IMG1); title('Original Hist');

% ----------------------------------------------
% Step1: 进行像素灰度级数统计
NumPixel2 = zeros(1,256);    %统计0-255灰度级数
for i = 1:h      
    for j = 1: w      
        NumPixel2(IMG2(i,j) + 1) = NumPixel2(IMG2(i,j) + 1) + 1;
    end      
end      

% Step2: 进行像素灰度级数累积统计    
CumPixel2 = zeros(1,256);      
for i = 1:256      
    if i == 1      
        CumPixel2(i) = NumPixel2(i);      
    else      
        CumPixel2(i) = CumPixel2(i-1) + NumPixel2(i);      
    end      
end   
subplot(232), imshow(IMG2); title('Manual HistEQ Image');
subplot(235), imhist(IMG2); title('Manual HistEQ Hist');

% ----------------------------------------------
% Matlab自带函数计算
IMG3 = zeros(h,w); 
IMG3 = histeq(IMG1);      % Matlab自带直方图均衡
subplot(233), imshow(IMG3); title('Matlab HistEQ Image');
subplot(236), imhist(IMG3); title('Matlab HistEQ Hist');


% ----------------------------------------------
figure;
subplot(121),bar(CumPixel); title('原图灰度级数累积');
subplot(122),bar(CumPixel2);title('拉伸后灰度级数累积');

上述代码采用了源码设计直方图均衡方式，同时和Matlab库进行对比查验结果。

其中直方图均衡时候，同时考虑了到了适合FPGA进行定点加速运算，主要可分为如下几步：

1）计算当前灰度图像0-255级数的像素数量

2）计算从0-255级数像素数量的累积值，即从0-h*w像素总量分布

3）将上述累计值除h*w后归一化，再扩大到像素取值范围255，以当前测试500*500的图像为例，可以合并计算/(h*w)*255=/980，那么进一步硬件思维分析，有以下几种思路：

        A）针对固定视频流，长款固定，如对精度要求不高，可直接除1024，即向右移动10bit，不过这样会损失较多的精度，可能导致异常。

        B）为了提高进度，除以980可以用一个除法器，根据余数结果判断是否大于490，再考虑是否进位，这在FPGA中的除法器有一定的面积代价，需要一堆组合逻辑及乘法器，但不得已而为之，为本篇中的最佳选择。

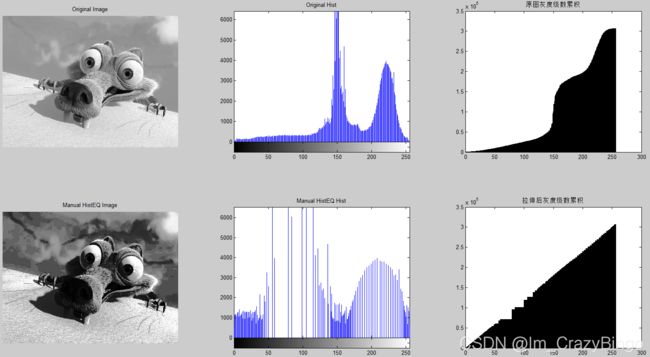
 如上图所示，为原图，及源码/matlab图像库分别进行图像均衡化的结果。其中结果对比图差不多，深究直方图还是略有差异，主要是我们采用了定点化的方式引起的误差，在可容忍的范围内。

最后，查看直方图均衡化之前，及均衡化之后的灰度级数累积图，如下所示，我们可见原图中灰度集中分布，再均衡化后，灰度级数在0-255内递增，因此达到了灰度拉伸的效果，增强了图像的对比度和辨识度，达到了我们本篇的需求。

---

4.直方图均衡FPGA实现

未完待续，敬请期待……

---

直方图均衡的缺点：

如果一幅图像整体偏暗或者偏亮，那么直方图均衡化的方法很适用。比如在静脉识别中，经850nm红外曝光，摄像头采集到的图像，通常为了防止过曝丢失信息，图像会偏暗一点，那么经过直方图均衡后可以简单快速的达到图像增强的效果，给后续算法增加了辨识度，如下图所示：

但直方图均衡化是一种全局处理方式，它对处理的数据不加选择，可能会增加背景干扰信息的对比度并且降低有用信号的对比度，进而引起图像的异常。因此主要有如下缺点：

1）变换后图像灰度级数减少，部分细节丢失

2）对于直方图有高峰时，拉伸后将出现对比度不自然的过分增强现象。

举例，如下图像中，对比度拉伸后图像对比度增强，虽然灰度级数拉伸后线性增加了，但却引起了局部过暗或者过曝，导致图像异常，丢失了很多细节，反而得不偿失。

 因此，针对局部的直方图均衡化方法，才能解决图像全局处理引起异常的问题。进一步的深入留给读者去研究，本片到此为止。

---

由于直方图均衡是在灰度域去实现的，主要针对亮度的拉伸，而RGB图像有三个通道的数据，可以分别对三个通道进行直方图拉伸，但这可能会引起图像色彩失真。因此，可以先转成YCbCr格式，对Y进行直方图均衡后，再转回RGB格式。

---

《Matlab数字图像处理-冈萨雷斯》图库下载地址：

 http://www.imageprocessingplace.com/DIP-3E/dip3e_book_images_downloads.htm

---

参考文献：

https://blog.csdn.net/charlene_bo/article/details/70263344?utm_source=blogxgwz3

https://blog.csdn.net/qq_15971883/article/details/88699218

---

I am CrazyBingo！

本文为《基于Matlab与FPGA的图像加速处理教程》中的章节，在正式出版前，我将率先在公众号/博客中给大家分享出来，请大胆指正！！！