读书笔记---《集体智慧编程》第3章：发现群组

1.关于聚类的理解

聚类实际上就是分类，对一些样本（样品）进行归类分组。本章第一个例子是对99篇博客进行聚类，也就是说每一篇博客便是一个样本。要分类就要有分类的标准（指标）。比如把人按地区、身高、体重分类，那地区、身高、体重就是指标。抽象地说，对样本 X ，设有p个指标，即 X=(X1,X2,⋯,Xp)T .在博客聚类的这个例子中，选取的分类指标是一些单词（这里暂时不管为什么要选这些单词），即为china,kids,music,yahoo,want等，总共706个，即有706个指标（变量）。统计出每篇博客中这些单词出现的次数，即为该篇博客的指标值（样本值）。

2.对博客进行聚类

对99篇博客中指定单词的统计结果存放到了blogdata.txt文件（随书文件中附带的有，也可以按照书中方法获取）中，用记事本打开看的话会比较乱，用Notepad++打开之后，截图如下：

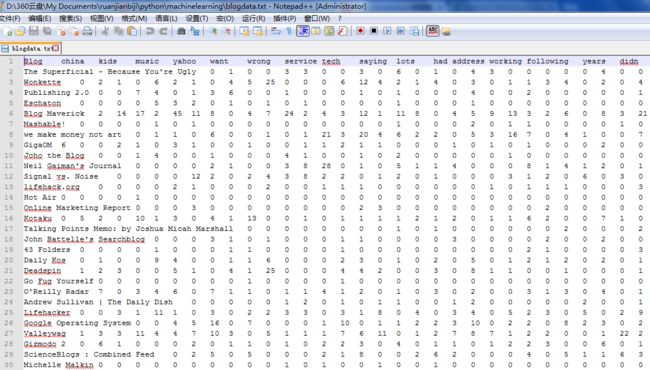
刚好这类似于R语言中数据框的结构，本来我想用R或者SAS来完成本章的任务，毕竟有现成的函数，不过在直接导入blogdata.txt这个文件时，均出现了问题，这个以后再解决。

在《数据分析方法》中，我们学了快速聚类法与谱系聚类法。下面来看本书中的算法。

2.1 分级聚类法

分级聚类法（Hierarchical Clustering）实际上就是谱系聚类法，具体原理和步骤可以参见《数据分析方法》一书。谱系聚类的关键是依据样品间的距离来定义类与类之间的距离。本章的分级聚类法实际上在计算类间距离时，采用的是重心距离，即用两类的重心之间的距离作为两类间的距离。

2.1.1读取数据

为了方便数据的处理，我们定义一个读取数据的函数，代码如下（使用版本为Python 3.3）

def readfile(filename):
    lines=[line for line in open(filename)]

    #第一行是列标题，也就是被统计的单词是哪些
    colnames=lines[0].strip().split('\t')[1:]#之所以从1开始，是因为第0列是用来放置博客名了
    rownames=[]
    data=[]
    for line in lines[1:]:
        p=line.strip().split('\t')
        #每行的第0列都是行名
        rownames.append(p[0])
        #剩余部分就是该行对应的数据
        data.append([float(x) for x in p[1:]])#data是一个列表，这个列表里每一个元素都是一个列表，每一列表的元素就是对应了colnames[]里面的单词
    return rownames,colnames,data

这里代码中的第一行

lines=[line for line in open(filename)]

中用了open函数，而原书代码是用了file函数，但我运行时出了问题，原书代码均是用Python 2.x编写的，因此会略有不同。此外，该函数采用元组返回值实现了返回多个函数值的办法。

此外，本书中经常使用reload函数，在Python 3.x中，应该这样使用

from imp import reload
reload(MyModule)

或者写为

import imp
imp.reload(MyModule)

因为在Python 3.x中，把reload内置函数移到了imp标准库模块中。它仍然像以前一样重载文件，但是必须导入它才能使用。

2.1.2计算紧密度（相似度）

这里要计算两篇博客（样本）的距离，可以通过计算两个样本 X(i) 和 X(j) 的Pearson相关系数 rij ，再令距离度量为

dij=1−|rij|

这样的话，两篇博客越相似（相关系数越大），其距离越小。

假设有两个变量 X 和Y，则总体的相关系数为

ρX,Y=Cov(X,Y)DX−−−√DY−−−√=E(XY)−E(X)E(Y)E(X2)−(EX)2−−−−−−−−−−−−−√E(Y2)−(EY)2−−−−−−−−−−−−−√

设样本观测数据为

(X1Y1X2Y2⋯⋯XnYn)

则样本相关系数为

r=SXYSXX−−−−√SYY−−−−√=∑i=1n(Xi−X¯)(Yi−Y¯)∑i=1n(Xi−X¯)2−−−−−−−−−−−√∑i=1n(Yi−Y¯)2−−−−−−−−−−√

进行适当化简可得

r=∑i=1nXiYi−∑i=1nXi∑i=1nYin∑i=1nX2i−(∑i=1nXi)2n−−−−−−−−−−−−−−⎷∑i=1nY2i−(∑i=1nYi)2n−−−−−−−−−−−−−⎷

计算代码如下：

from math import sqrt
def pearson(v1,v2):
    #先求和
    sum1=sum(v1)
    sum2=sum(v2)

    #求平方和
    sum1Sq=sum([pow(v,2) for v in v1])
    sum2Sq=sum([pow(v,2) for v in v2])

    #求乘积之和
    pSum=sum([v1[i]*v2[i] for i in range(len(v1))])

    #计算pearson相关系数
    num=pSum-(sum1*sum2/len(v1))
    den=sqrt((sum1Sq-pow(sum1,2)/len(v1))*(sum2Sq-pow(sum2,2)/len(v1)))
    if den==0:return 0

    return 1.0-num/den

2.1.3聚类过程

这里采用面向对象的思维进行编程，将每一篇博客看成是一个对象，为此定义一个类，代码如下：

class bicluster:
    def __init__(self,vec,left=None,right=None,distance=0.0,id=None):
        self.left=left
        self.right=right
        self.vec=vec #就是词频列表
        self.id=id
        self.distance=distance

下面开始聚类的计算。在《数据分析方法》中，我们是先计算出了距离矩阵，然后利用递推的方法逐步计算。这里，我们也编写一个hcluster函数直接进行计算，该函数为一个列表数组（就是在读取数据时返回的data）和一个距离函数（Python的函数式编程确实也很不错），最后返回一个bicluster的对象，只有一个，但是这个对象是根节点，如果扩展其左右孩子，最后会得一个粗略的树状图。代码如下：

def hcluster(rows,distance=pearson):
    distances={} #每计算一对节点的距离值就会保存在这个里面,这样避免了重复计算
    currentclustid=-1

    #最开始的聚类就是数据集中的一行一行,每一行都是一个元素
    #clust是一个列表,列表里面是一个又一个bicluster的对象
    clust=[bicluster(rows[i],id=i) for i in range(len(rows))]

    while len(clust)>1:
        lowestpair=(0,1)#先假设lowestpair是0和1号
        closest=distance(clust[0].vec,clust[1].vec)#同样将0和1的pearson相关度计算出来放着
        #遍历每一对节点,找到pearson相关系数最小的
        for i in range(len(clust)):
            for j in range(i+1,len(clust)):
                #用distances来缓存距离的计算值
                if(clust[i].id,clust[j].id) not in distances:
                    distances[(clust[i].id,clust[j].id)]=distance(clust[i].vec,clust[j].vec)
                d=distances[(clust[i].id,clust[j].id)]
                if d#找到这一次循环的最小一对后,产生新的枝节点.先计算出这个新的枝节点的词频（重心）
        mergevec=[(clust[lowestpair[0]].vec[i]+clust[lowestpair[1]].vec[i])/2.0 for i in range(len(clust[0].vec))]

        #建立新的聚类
        newcluster=bicluster(mergevec,left=clust[lowestpair[0]],right=clust[lowestpair[1]],distance=closest,id=currentclustid)

        #不在初始集合中的聚类,其id设置为负数
        currentclustid-=1
        del clust[lowestpair[1]]
        del clust[lowestpair[0]]
        clust.append(newcluster)

    #当只有一个元素之后,就返回,这个节点相当于根节点
    return clust[0]

2.1.4粗略的树状图

这里只是利用了缩进而已，先编写函数：

def printclust(clust,labels=None,n=0):
    #利用缩进来建立层级布局
    for i in range(n):print(' ',end=" ")
    if clust.id<0:
        #负数代表这是一个分支
        print('-')
    else:
        #正数代表这是一个叶节点
        if labels==None: print(clust.id)
        else:print(labels[clust.id])
    if clust.left!=None:printclust(clust.left,labels=labels,n=n+1)
    if clust.right!=None:printclust(clust.right,labels=labels,n=n+1)

然后在执行如下代码即可画出粗略的树状图，这里就不展示了。

blognames,words,data=readfile('blogdata.txt')
clust=hcluster(data)
printclust(clust,labels=blognames)

要注意的是与原书代码不同的地方在于print函数，Python 3.x与Python 2.x关于print的主要区别如下：

2.X: print "The answer is", 2*2 
3.X: print("The answer is", 2*2) 
2.X: print x,             # 使用逗号结尾禁止换行 
3.X: print(x, end=" ")    # 使用空格代替换行 
2.X: print                # 输出新行 
3.X: print()              # 输出新行 
2.X: print >>sys.stderr, "fatal error" 
3.X: print("fatal error", file=sys.stderr) 
2.X: print (x, y)         # 输出repr((x, y)) 
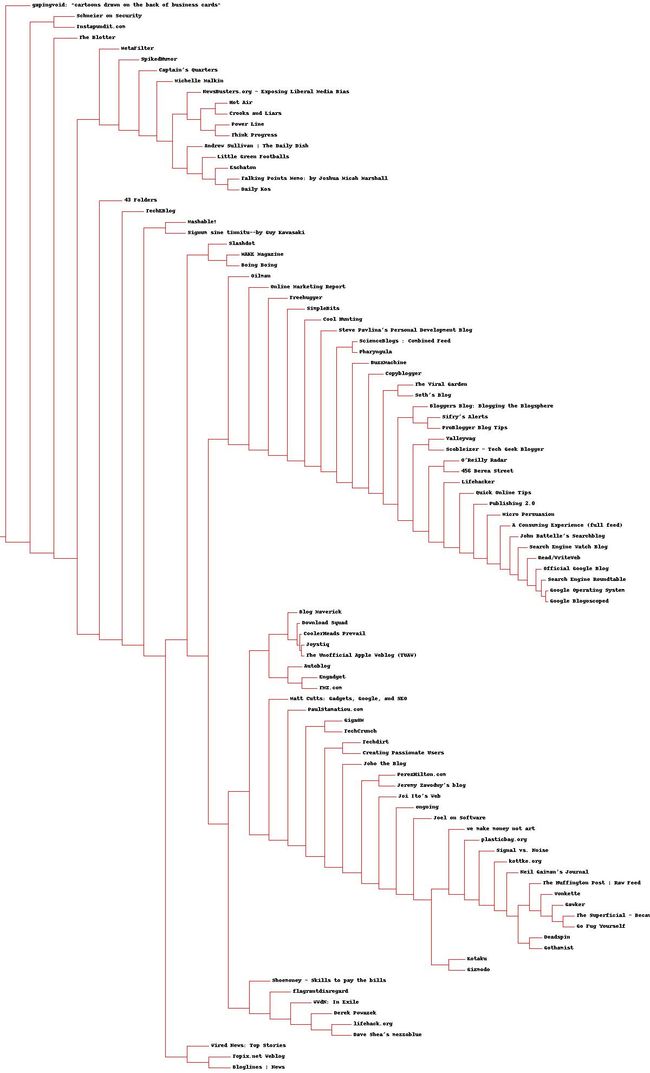
3.X: print((x, y))        # 不同于print(x, y)! 

2.1.5精细的树状图

实际上就是我们学过的谱系图。为了用Python画出这个图，需要用到Python的图像处理模块PIL（Python Image Library），其并不支持Python3，但网上有人把它重新编译生成Python3下可安装的exe了，比如我下载的就是PIL-1.1.7.win32-py3.3.exe，直接搜索PIL py3.3就出来了，然后安装即可。

画图的过程还是很复杂的，具体可见这篇博客
画树状图

总体代码如下：

from PIL import Image,ImageDraw

def getheight(clust):
    #这是一个叶节点吗？若是,则高度为1
    if clust.left==None and clust.right ==None:return 1
    #否则,高度为每个分支的高度之和
    return getheight(clust.left)+getheight(clust.right)


def getdepth(clust):
    #一个叶节点的距离是0.0,这是因为叶节点之后就没有了,将其放在最左边也没事
    if clust.left==None and clust.right ==None:return 0

    #而一个枝节点的距离等于左右两侧分支中距离较大的那一个
    #加上自身距离：所谓自身距离,与就是某节点与两一节点合并时候的相似度
    return max(getdepth(clust.left),getdepth(clust.right))+clust.distance

def drawdendrogram(clust,labels,jpeg='clusters.jpg'):
    #高度和宽度
    h=getheight(clust)*20
    w=1200
    depth=getdepth(clust)

    #我们固定了宽度,所以需要对每一个节点的横向摆放做一个缩放,而不像高度一样,每一个叶节点都分配20
    scaling=float(w-150)/depth

    #新建一张白色的背景图片
    img=Image.new('RGB',(w,h),(255,255,255))
    draw=ImageDraw.Draw(img)

    draw.line((0,h/2,10,h/2),fill=(255,0,0)) #仅仅是画了一个起点

    #画第一个节点
    drawnode(draw,clust,10,(h/2),scaling,labels)
    img.save(jpeg,'JPEG')

def drawnode(draw,clust,x,y,scaling,labels):
    if clust.id<0:
        h1=getheight(clust.left)*20 #两个分支的高度
        h2=getheight(clust.right)*20

        top=y-(h1+h2)/2 #如果是第一次画点的话,top居然是最高点,也就是等于0,是上面边界.针对某一个节点,其高度就是左节点的高度加右节点的高度
        bottom=y+(h1+h2)/2 #这个确实也是下边界。

        #线的长度
        ll=clust.distance*scaling

        #聚类到其子节点的垂直线
        draw.line((x,top+h1/2,x,bottom-h2/2),fill=(255,0,0))

        #连接左侧节点的水平线
        draw.line((x,top+h1/2,x+ll,top+h1/2),fill=(255,0,0))

        #连接右侧节点的水平线
        draw.line((x,bottom-h2/2,x+ll,bottom-h2/2),fill=(255,0,0))

        #调用函数绘制左右节点
        drawnode(draw,clust.left,x+ll,top+h1/2,scaling,labels)
        drawnode(draw,clust.right,x+ll,bottom-h2/2,scaling,labels)
    else:
        #如果这是一个叶节点,则绘制节点的标签.其实现在突然觉得这种思路非常好,绘制的是标签,本题中绘制的博客名字
        draw.text((x+5,y-7),labels[clust.id],(0,0,0))

blognames,words,data=readfile('blogdata.txt')
clust=hcluster(data)
drawdendrogram(clust,blognames,jpeg='分级聚类图.jpg')

画出来的图如下：

2.2 列聚类

这里也就是将整个blogdata.txt中的数据集进行了转置，使列（也就是单词）变成了行，其中的每一行都对应一组数字，这组数字指明了某个单词在每篇博客中出现的次数。转置后在调用上面的函数即可。

至于这种方式聚类出来的结果有何意义，需要结合具体情况分析。

2.3 K− 均值聚类

K− 均值聚类（K-Means Clustering）实际上就是我们学过的快速聚类法，原理和步骤可参见《数据分析方法》，只不过本章中的 K− 均值聚类中最初的$k$个聚点是随机生成的。

未完待续