机器学习算法基础 Day4

概率基础

概率定义为一件事情发生的可能性

联合概率和条件概率

问题

1、女神喜欢的概率？

4/7

2、职业是程序员并且体型匀称的概率？

P(程序员， 匀称) = 3/7 * 4/7 = 12/49

3、在女神喜欢的条件下，职业是程序员的概率？

P(程序员|喜欢) = 2/4

4、在女神喜欢的条件下，职业是产品，体重是超重的概率？

P(产品， 超重|喜欢) = P（产品|喜欢）P（超重|喜欢）= 1/2 * 1/4 = 1/8

朴素贝叶斯公式

 

问题：从上面的例子我们得到娱乐概率为0，这是不合理的，如果词频列表里面有很多出现次数都为0，很可能计算结果都为零 

sklearn朴素贝叶斯实现API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

• 朴素贝叶斯分类
• alpha：拉普拉斯平滑系数

朴素贝叶斯分类

alpha：拉普拉斯平滑系数

案例

sklearn20类新闻分类

20个新闻组数据集包含20个主题的18000个新闻组帖子

流程

加载20类新闻数据，并进行分割

生成文章特征词

朴素贝叶斯estimator流程进行预估

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report

def naviebayes():
    """
    朴素贝叶斯进行文本分类
    :return: None
    """
    news = fetch_20newsgroups(subset='all')

    # 进行数据分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)

    # 对数据集进行特征抽取
    tf = TfidfVectorizer()

    # 以训练集当中的词的列表进行每篇文章重要性统计['a','b','c','d']
    x_train = tf.fit_transform(x_train)

    print(tf.get_feature_names())

    x_test = tf.transform(x_test)

    # 进行朴素贝叶斯算法的预测
    mlt = MultinomialNB(alpha=1.0)

    #print(x_train.toarray())

    #输入训练集特征值和目标值
    mlt.fit(x_train, y_train)

    y_predict = mlt.predict(x_test)

    print("预测的文章类别为：", y_predict)

    # 得出准确率
    print("准确率为：", mlt.score(x_test, y_test))

    print("每个类别的精确率和召回率：", classification_report(y_test, y_predict, target_names=news.target_names))

    return None

if __name__ == "__main__":
    naviebayes()

 

结果：

预测的文章类别为： [ 5  9 11 ...  5 17  7]
准确率为： 0.8461375212224108
每个类别的精确率和召回率：                          

precision    recall  f1-score   support

             alt.atheism       0.87      0.71      0.78       201
           comp.graphics       0.86      0.78      0.82       235
 comp.os.ms-windows.misc       0.88      0.81      0.84       253
comp.sys.ibm.pc.hardware       0.72      0.86      0.78       238
   comp.sys.mac.hardware       0.92      0.88      0.90       234
          comp.windows.x       0.94      0.83      0.88       258
            misc.forsale       0.94      0.69      0.79       248
               rec.autos       0.92      0.92      0.92       251
         rec.motorcycles       0.94      0.95      0.95       246
      rec.sport.baseball       0.95      0.95      0.95       255
        rec.sport.hockey       0.95      0.97      0.96       274
               sci.crypt       0.73      0.97      0.84       236
         sci.electronics       0.87      0.81      0.84       228
                 sci.med       0.95      0.92      0.93       237
               sci.space       0.87      0.95      0.91       242
  soc.religion.christian       0.55      0.98      0.71       253
      talk.politics.guns       0.77      0.97      0.86       229
   talk.politics.mideast       0.86      0.96      0.91       222
      talk.politics.misc       0.97      0.58      0.73       201
      talk.religion.misc       1.00      0.16      0.28       171

                accuracy                           0.85      4712
               macro avg       0.87      0.83      0.83      4712
            weighted avg       0.87      0.85      0.84      4712

朴素贝叶斯分类优缺点

分类模型的评估

estimator.score()
一般最常见使用的是准确率，即预测结果正确的百分比

混淆矩阵

在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

其他分类标准，F1-score，反映了模型的稳健性

分类模型评估API

sklearn.metrics.classification_report

classification_report

sklearn.metrics.classification_report(y_true, y_pred, target_names=None)

y_true：真实目标值

y_pred：估计器预测目标值

target_names：目标类别名称

return：每个类别精确率与召回率

模型的选择与调优
交叉验证：为了让被评估的模型更加准确可信
网格搜索

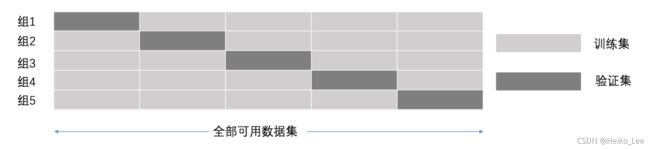
交叉验证过程
交叉验证：将拿到的数据，分为训练和验证集。以下图为例：将数据分成5份，其中一份作为验证集。然后经过5次(组)的测试，每次都更换不同的验证集。即得到5组模型的结果，取平均值作为最终结果。又称5折交叉验证

超参数搜索-网格搜索

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

超参数搜索-网格搜索API：

sklearn.model_selection.GridSearchCV

• 对估计器的指定参数值进行详尽搜索

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)

estimator：估计器对象

param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}

cv：指定几折交叉验证

fit：输入训练数据

score：准确率

结果分析：
best_score_:在交叉验证中测试的最好结果

best_estimator_：最好的参数模型

cv_results_:每次交叉验证后的测试集准确率结果和训练集准确率结果

# 构造一些参数的值进行搜索
    param = {"n_neighbors": [3, 5, 10]}

    # 进行网格搜索
    gc = GridSearchCV(knn, param_grid=param, cv=2)

    gc.fit(x_train, y_train)

    # 预测准确率
    print("在测试集上准确率：", gc.score(x_test, y_test))

    print("在交叉验证当中最好的结果：", gc.best_score_)

    print("选择最好的模型是：", gc.best_estimator_)

    print("每个超参数每次交叉验证的结果：", gc.cv_results_)

结果：

在测试集上准确率： 0.4773049645390071
在交叉验证当中最好的结果： 0.4459331651954603
选择最好的模型是： KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=10, p=2,
                     weights='uniform')
每个超参数每次交叉验证的结果： {'mean_fit_time': array([0.02700055, 0.02850068, 0.02848065]), 'std_fit_time': array([0.00101984, 0.00249922, 0.00150144]), 'mean_score_time': array([0.68606126, 0.75706172, 0.79506814]), 'std_score_time': array([0.02999103, 0.02998281, 0.00400817]), 'param_n_neighbors': masked_array(data=[3, 5, 10],
             mask=[False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}], 'split0_test_score': array([0.42197352, 0.43537201, 0.44293821]), 'split1_test_score': array([0.42260404, 0.43978562, 0.44892812]), 'mean_test_score': array([0.42228878, 0.43757881, 0.44593317]), 'std_test_score': array([0.00031526, 0.00220681, 0.00299496]), 'rank_test_score': array([3, 2, 1])}