后缀自动机（SAM）

最近想学字符串，断断续续好一段时间也总算是把后缀自动机给啃下来了。这里按自己的思路，系统的梳理一下这个功能强大的工具。

后缀自动机的模型

这里先把我们的目的给讲清楚。先建立一个自动机，也就是一个图，通过这个图的点边信息我们可以把整个字符串的所有功能全部储存下来。
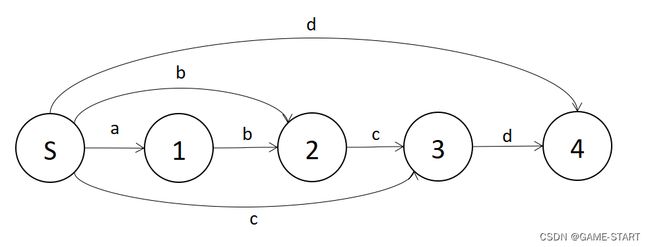
首先让我们看一下一个字符串abcd的后缀自动机建立出来的样子

在这里s为起始点，总共有1，2，3，4四个状态，你会发现从s点开始随意跑，再随意以1，2，3，4的某个状态为终点，收集路径上所有的点权信息，你可以得到abcd的任意连续字串。

你会发现这样的操作和有个模型非常像，没错，就是字典树。
不过我们建立的自动机要求更高。

后缀自动机要求我们的节点和边数要尽可能的少，这样可以最大程度上把我们的时间复杂度和空间复杂度降下去。而通过那些算法巨佬的研究，则是成功把该复杂度讲到O(n)级别的，节点状态量最多大概2n左右，orz。

后缀自动机的重要性质

endpos

在这里我们需要先引入一个对于后缀自动机来说的重要概念，可以说这个算法都是建立在这个概念上，也就是endpos函数。

这个函数的返回值是对应字符串在原字符串出现的所有位置的末尾值。
字符串abcabcd，起始位子从1开始。

对于这个字符串，endpos(‘a’)={1,4}，因为a字符出现在1，4两个位置。endpos(“ab”)={2，5}，因为ab字符串出现在1-2，4-5两个位置，但只返回末尾位置，所以是2，5。

然后如果我们把他所有的字串的endpos函数全给写出来，会发现有一些字符串的返回值相同，那么我们就把这些字符串归为一组。

一个字符串不同字串的数目最多为n^2的数量，但是按照我们上述方式分组之后，我们的组数最多也就是2n左右。这里先不证明，可以感性理解一下。

如果你记性不错的话，应该注意到了我上面说了我们后缀自动机的状态量最多2n左右，这里的组数刚好也是2n左右。没错，我们上述的每一个状态节点，就是我们后面endpos的一个分组形式。

那么接下来就是解释为什么要这样分组了，当然我只能给你倒向解释这样分组带来的性质，没有办法通过这些性质来推导出这样的分组方式。
(主要网上也没大佬讲一讲啊 QAQ)

还是字符串abcabcd，我们会发现c，bc，abc的endpos值是一样的，所以他们仨在一组里面，按照字符长度进行排序，会有两个性质显而易见，但不易证 。

一个是每个元素的长度唯一且连续。无论你怎么找样例，你都不可能找到一组endpos集合里面有两个相同长度的元素，或者存在元素长度不是连续的集合(长度连续的意思是，元素的长度依次为i，i+1,i+2…i+n)。

另外一个性质是，按元素长度从小到大排序好后，前一个元素是后一个元素的后缀，或者换句话说，该集合内的所有元素可以视为最短的元素每次增加一个新的字符而构成，所有元素都是最长元素的后缀。这样的话我们只要保存三个信息就可以得到该集合的所有信息，最短元素长度，最长元素长度，以及最长元素本身信息。其实在后续搭建sam的时候，每个节点只用储存最长元素长度即可，这个后面再说。

以上两个性质都有严密的论证，也不长，如果想要看一下可以搜一下，这里就不赘述了。

接下来另外一个性质则是集合与集合之间的关系，这个性质也是线性搭建sam的重要性质。不同的集合存在包含关系。

举个栗子。

字符串dcbacb，endpos(b)={3,6},endpos(cb)={3,6},endpos(acb)={6}。
首先这仨都存在后缀关系，但由于我们的分组原则，b，cb分到一组，acb分到另一组。这里你会发现，如果两个字符串存在后缀关系，较长的字符串的endpos返回值一定是较短的那个的子集。这个应该很好理解，字符串越长，限制越多，他的endpos就会越少，而且一定是在原先的基础上变少而不会变多。因为字符串能出现的位置，他的后缀一定会出现，且数目只会大于等于，不可能会少。

由该性质我们推得一个推论，一连串存在后缀关系的长度连续的字符串，他们分组后的信息具有包含传递的信息。比如对于某一段字符串1到r，他们可以分为1 ~ r，2 ~ r，…，r ~ r，共r-l+1组，对于任意前后两个挨着的字符串，他们要么从属于同一个分组内，要么是两个相邻的分组。

这里的说法可能会有一点抽象，那就接着看下去，在后面建图的时候会利用起来。

后缀自动机的构建

讲了这么久，终于开始搭了。

我们先介绍一下我们的节点里面需要存什么值

struct node{
	int len,fa;
	int ch[26];
}

嗯，莫得啦。就这三个东西。

len代表该节点状态内最长的字符串的长度，换句话说，按照我们上述分组之后，这个集合中最长字符串的长度。

fa则是这个集合的上一个状态是谁。

你看，我们上面不是刚讲过一连串的字符串，1 ~ r，2 ~ r，…，r ~ r。我们给他们分组，这里括号内的为一组，可以写成下面这样
(1 ~ r，2 ~ r，3 ~ r)，（4 ~ r，5 ~ r）…（r-1 ~ r，r ~ r）

每个集合里面的最长字符串就是该集合里的第一个，并且前一组的fa就是后一组。

然后ch则是代表这个集合一条指出去的边，ch[0]则是代表指出去一个边权为a的边，以此类推，之后出现了别的额外边权再加就好。

然后这里我们开始搭建，从一个起点s开始。这里采取的搭建方式是倍增法，在原图的基础上一个个加入新点，再修改原图得到。

假设我们已经搭建好了abc的后缀自动机，如下图

接下来我们怎么搭建abcd呢。

首先我们要知道，在原先的后缀自动机里面，他最多最多只能表示出abc这个字符串，abcd这个字符串他是不可能表示出来的，我们压根就没建出这个状态。所以我们必须要加入一个新的状态，也就是4号点，这个点就代表abcd所在的集合。

当我们加入一个新的字符d之后，他会在原先的基础上带入d，cd，bcd，abcd四个字符串状态。接下来我们就是要修改原图，把上述新的状态加入图中。

sam现在的状态是4，上一个状态是3。引入了d字符，我们会先检查3.ch[3]是否有连接出去，这个是肯定没有的，因为状态3中有adc，如果有d连接出去，那么他走过去就是abcd的这个状态，说明abcd这个状态已经存在了。但是因为这个状态我们是刚引进的，原图中不可能会有，所以我们就让3.ch[3]=4。也就是3加了个d状态之后是4。

这里我们先观察原图，3的状态里面包含了c,bc,abc。这里连接了d之后他可以推导出状态cd，bcd，abcd三个状态。还差个d状态我们没有表达出来，那么我们就找3状态的fa节点是谁。我们上面不是说过了吗l ~ r 和 l+1 ~ r如果不在同一个集合里面，那么l ~ r 的父节点就是 l+1 ~ r。这样我们就能每次找父节点，把上一个状态找到3状态包含了 1-3，2-3，3-3，那么他的上一个fa节点也就是4-3这个不存在状态的节点，是个空集，也就是s起点。那么s起点加一个d连接到4状态，就表达了空集加上d，也就是d这个状态。就此abcd的sam搭建好了。
(可喜可贺可喜可贺！)

搭建完如上图。

那么那么那么，细心的你一定发现了华点。没错，我们之前讨论的都是不存在这个新的边搭建出去的情况。那如果这个边已经存在了呢？那该怎么办。

那么我们首先要做到的就是先别急，先冷静分析一下，这个边连接出去的有无代表着什么意义。

那么比如上一个状态是n，我们这次假设加入一个a字符，新建了一个n+1的状态。我之前也说过了，那么n.ch[0]这个边是一定不存在的。因为一旦存在了，就代表原图已经存在了这个状态了，而最新状态一定是原来图中没有的，所以这个边一定要连。从这里就可以知道，当我们一直往回找fa节点的时候，一旦某一个点存在对应的边了，那就说明该种情况原本的自动机已经囊括了，不需要重新建边。

但是这样也出现了一个问题。如果你现在已经了解了后缀自动机的节点意义，你就会发现，如果原本自动机已经包含了加入了的字符串，那么对于这个自动机来说，这个节点内部的情况就会改变。

再举个栗子，字符串abcc。当我们完成了abc的自动机建立，节点3里面有c，bc，abc。因为他们的endpos都是3，可是当我加入c的时候，你会发现c的endpos从3变成了3，4。而bc和abc还是3，那么这里的c应该是要和原来的节点分来，变成c以及bc，abc两个节点。

那么还有一种可能，如果有字符串abcabc，你会发现从abcab到abcabc，abc，bc，c的endpos变了，可是这几个变完之后还是在同一个集合里面，说明这个节点需要变化，但是不需要切割。

这里我们结合代码和图，可能会好理解一点。

这里的代码大概是这样的：

int p=lst,np=lst=++tot;
nd[np].len=nd[p].len+1;
for(;p&&!nd[p].ch[x];p=nd[p].fa)nd[p].ch[x]=np;

p为上次末尾新建的点，np则是这次建的点。新建的np点的集合内最长字符串肯定是上次这个状态+1。
每次p都走p的fa节点，如果这个点没有对应的x边连出去，那么就连一个边到np节点。

if(!p)nd[np].fa=1;
//*1
else{
	if(nd[nd[p].ch[x]].len==nd[p].len+1)nd[np].fa=nd[p].ch[x];
	//*2
	else{
		int q=nd[p].ch[x],nq=++tot;
		nd[nq]=nd[q];
		nd[nq].len=nd[p].len+1;
		nd[q].fa=nd[np].fa=nq;
		for(;p&&nd[p].ch[x]==q;p=nd[p].fa)nd[p].ch[x]=nq;
	}
	//*3
}

如果我在路径上一直没找到有找到有x连出去的边，那就一直连，然后新节点的父节点直接变到s起始节点。这里是上述的情况*1。

为什么这里fa节点可以直接连到s而不是临近的上一个节点？这个步骤相当于并查集的归并操作。这个跳fa的操作可以理解为压缩地遍历一个串的所有后缀。在这里，p=p.fa即从长到短遍历旧串的所有后缀。

这里需要思考一下。

第二个情况，如果存在某个节点p，连出去的p是存在的，并且连出去的目标节点的最长长度刚好为p点的最长长度+1。为什么要注意这个呢？因为首先，节点p是新加入节点往回跳的后缀路径上的某个点，也就是节点p加上一个x刚好就是np节点的后缀，如果
nd[nd[p].ch[x]].len==nd[p].len+1
也就是这个目标节点内部的点都是刚刚好加一个x变成np的后缀。所以这里的情况已经存在，只要把np的fa改成这个点就行。

第三个情况，如果连出去的这个点的节点，设为q，最长长度是比p要长，那么对于q.len+1长度的点还是满足情况2的，比这个长度长的点是不满足的，那我们就新加一个点，分成不大于q.len+1的节点和大于这个长度的节点。同时分割开的两个节点之间还是存在连线关系，所以这里新拉出去的点应该变成原先节点的fa。

上述三种情况比较复杂，大概率看到这里的你是看不懂的吧。自己是懂了，但是对我个人而言用文字有点难以描写，所以你可以先看了我这篇文章了解了大概之后再去看这篇文章。

上面的一坨可以不用看，直接看下面三种情况的分类代码就好，讲得还是比较详细的。

这篇文章之后应该还是会慢慢修改。