ROC与AUC 的理解和python实现

评估一个二分类的分类器的性能指标有：准确率、查准率（precision）、查全率（recall）、F1值 以及 ROC 和 AUC 等。前面几个比较直观，而 ROC和AUC 相对抽象一点。

1. 混淆矩阵

首先一个用分类器预测完后，会得到一个二分类的混淆矩阵：

多分类的混淆矩阵这里暂不考虑，但是分析是类似的。

实际（多分类）	预测
	类1	类2	类3
类1	43	2	0
类2	5	45	1
类3	2	3	49

（1） 准确率
所有预测正确的样本占所有样本的比例，但这个指标在类别比例不平衡时不太恰当。

（2）查准率(Precision)
直观理解为： 在所有预测为正例中，真正正例的比例。（有点绕，多读几遍就好）
$$P=\frac{TP}{TP+FP}$$

（3） 查全率(Recall)
直观理解为： 在所有真实的正例中，预测为正例的比例。
$$R=\frac{TP}{TP+FN}$$

（4）F1-score
由于 Precision 和 Recall是一对不可调和的矛盾，很难同时提高二者，也很难综合评价。故提出 F1 来试图综合二者，F1是P和R的调和平均（harmonic mean）：
$$\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})\to F1=\frac{2PR}{P+R}$$

2. 什么是ROC曲线

先有一个概念：很多学习器能输出一个实值或者概率预测，然后设定一个阈值，高于阈值为正类，反之负类。分类的过程就是设定阈值，并用阈值对预测值做截断的过程，当这个阈值发生变动时，预测结果和混淆矩阵就会发生变化，最终导致一些评价指标的值的变化。

Wikipedia上对ROC曲线的定义：

In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied.

重点就在于这个“as its discrimination threashold is varied”。

在进一步了解ROC之前，首先定义两个指标：

• 真正例（True Positive Rate，TPR），表示所有正例中，预测为正例的比例：
  $$TPR=\frac{TP}{TP+FN}$$

• 假正例（False Positive Rate，FPR），表示所有负例中，预测为正例的比例：
  $$FPR=\frac{FP}{TN+FP}$$

以 FPR 为横坐标，TPR 为纵坐标，那么ROC曲线就是改变各种阈值后得到的所有坐标点 (FPR,TPR) 的连线，画出来如下。红线是随机乱猜情况下的ROC，曲线越靠左上角，分类器越佳。

真实情况下，由于数据是一个一个的，阈值被离散化，呈现的曲线便是锯齿状的，当然 数据越多，阈值分的越细，”曲线”越光滑。

3. AUC是什么

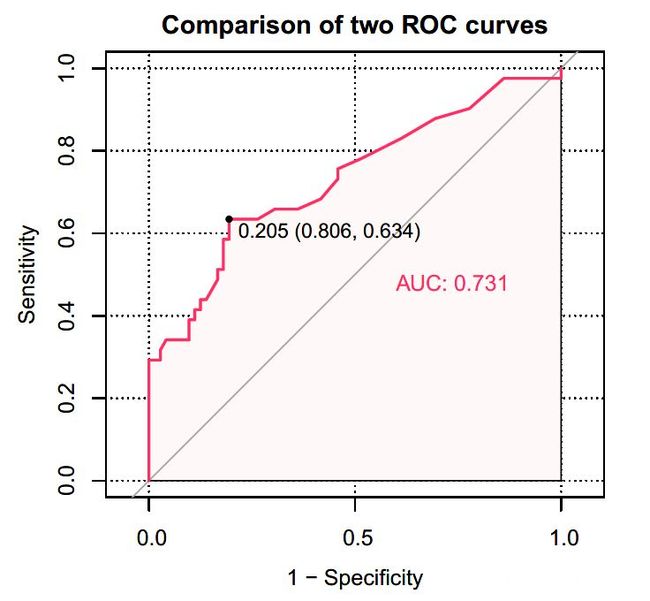
AUC（Area Under Curve）就是ROC曲线下的面积。
AUC的计算有两种方式，梯形法和ROC AUCH法，都是以逼近法求近似值。

（1）AUC的含义

根据(Fawcett, 2006)，AUC的值的含义是：

The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.

有点绕，解释一下：首先 AUC值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率，就是AUC值。当然，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。

用AUC判断分类器（预测模型）优劣的标准：

• AUC = 1 ，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。
• AUC值越大的分类器，正确率越高。
  

4. 为什么使用ROC曲线

既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：
当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。
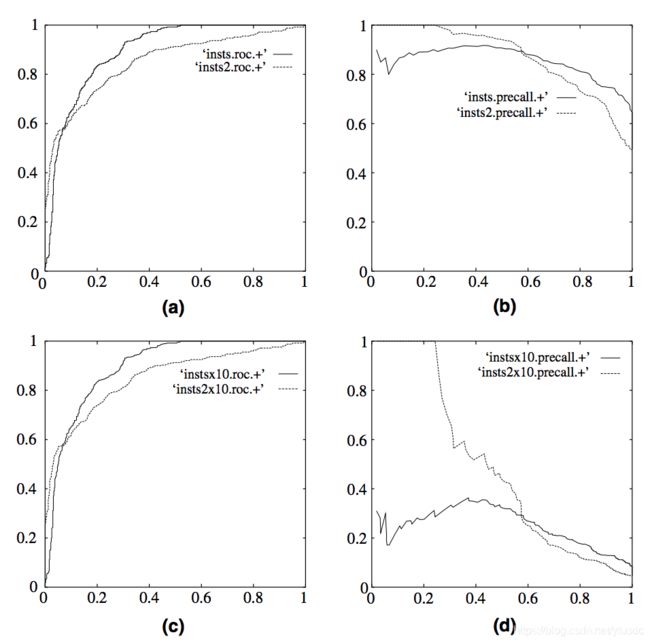
在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和 Precision-Recall 曲线的对比：

在上图中，(a)和©为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，©和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。

5. 用python的sklearn：绘制ROC曲线+求AUC

(1). 分别求ROC和AUC

• 求 ROC：sklearn.metrics.roc_curve()
• 求 AUC：sklearn.metrics.auc()

import numpy as np
from sklearn.metrics import roc_curve, auc

y = np.array([1, 1, 1, 1, 1,
              2, 2, 2, 2, 2])
y_proba = np.array([0.1, 0.4, 0.4, 0.3, 0.5,
                    0.4, 0.6, 0.7, 0.8, 0.5])   # probability of prediction as positive

fpr, tpr, thresholds = roc_curve(y, y_proba, pos_label=2)
auc = auc(fpr, tpr)

>>> fpr
array([0. , 0. , 0.2, 0.6, 1. ])
>>> tpr
array([0.2, 0.6, 0.8, 1. , 1. ])
>>> thresholds
array([0.8, 0.6, 0.5, 0.4, 0.1])
>>> auc
>>> 0.9

将 fpr 和 tpr 的值用matplotlib绘制即得 ROC 曲线。如下图：

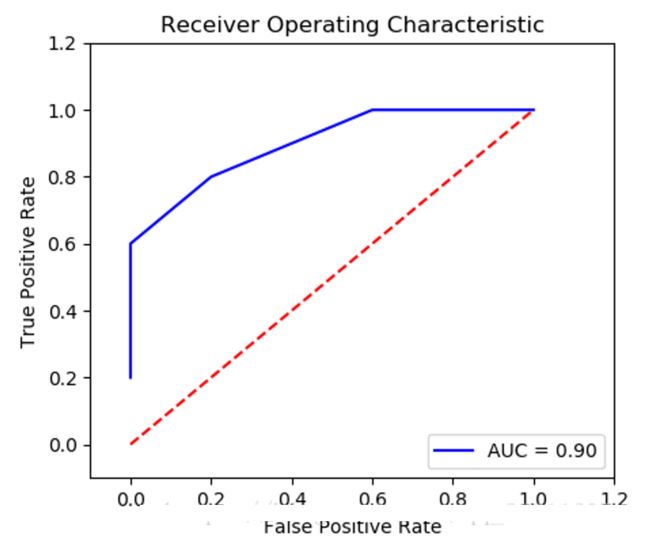
(2). 直接求AUC

也可以用 sklearn.metrics.roc_auc_score() 直接求得AUC

import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
roc_auc_score(y_true, y_scores)

# 0.75

6. 原文链接

原文链接：http://iloveeli.top:8090/archives/roc-yu-auc