一、词向量模型
因为计算机不能理解词语,所以我们需要用词向量表示一个词。
词向量有一个发展历程:从one-hot到word embedding。
1 one-hot
设词典的大小为n(词典中有n个词),假如某个词在词典中的位置为k,则设立一个n维向量,第k维置1,其余维全都置0。这个思想就是one-hot编码,中文叫独热编码(茫茫0海中有一个1,不就是孤独的热点吗)。
比如这里有三句话,即三个样本:
“我喜欢你”;
“你喜欢你的狗狗”;
“你是狗狗”。
假设已经分词完成,那么如果我们要从这三个样本中挖掘信息的话,根据词袋模型的思想:
首先就要将这些句子中出现过的词构建一个词典。这个词典依次包含[我,喜欢,你,的,是,狗狗]这六个词。根据one-hot编码,“我”就会被编码为[1,0,0,0,0,0],而“喜欢”就被编码为[0,1,0,0,0,0],以此类推。
那么如何继续推进,利用one-hot编码来生成特征向量呢?
一个样本的特征向量等于该样本中的每个单词的one-hot向量直接相加。这三个样本的特征向量便会表示为:
我喜欢你:[1,1,1,0,0,0]
你喜欢你的狗狗:[0,1,2,1,0,1]
你是狗狗:[0,0,1,0,1,1]
其中,第二个句子中“你”出现了两次,因此第三维的值为2。但是注意一下,在有的机器学习模型,比如贝努利分布的朴素贝叶斯模型中,仅考虑每个词出现与否,此时第二个句子的词袋模型就变成了[0,1,1,1,0,1]。
看,特征向量构建完成啦,剩下的就交给机器学习吧
(原文链接:https://blog.csdn.net/xixiaoyaoww/article/details/105459590)
优点:思路简单。
缺点:一般词库是一个很大的库。例如词库会达到30万,那就需要一个30万维度的向量表示一个词。这样计算量很大。同时整个矩阵会是一个稀疏矩阵。极大的浪费内存与计算力。
2 TF-IDF
第二种是使用词出现的频率,以及逆文档频率表示一个词。
TF=某个词在文章中出现的频率/文章的总次数
IDF=log{语料库的总文档数/出现该词的文档数}
T F − I D F = T F ∗ I D F TF-IDF=TF*IDF TF−IDF=TF∗IDF
对于一句话,就是把句子中的词的TF-IDF拼起来,形成一个向量。
优点:简单快速,结果比较符合实际
缺点:单纯考虑词频,忽略了词与词的位置信息以及词与词之间的相互关系。
3 bi-gram和n-gram
优点:考虑了词的顺序
缺点:词表膨胀,无法衡量向量之间的相似性
4 word embedding
用固定长度的向量表示一个词。
这个向量需要能够保证相似的词,距离近;在不同语言中,空间分布很相似;向量能够做加减运算: V k i n g − V q u e e n + V w o m e n = V m a n V_{king}-V{queen}+V_{women}=V_{man} Vking−Vqueen+Vwomen=Vman
流行的训练算法是Word2Vec。具体有两种形式:CBOW和skip-gram。它们很类似,这里介绍skip-gram。
- skip-gram
用中心词预测周围单词。
输入第t个词,用一层的神经网络,预测周围的词,也就是第t-2个,t-1个,t+1个,t+2个…。
对于模型:
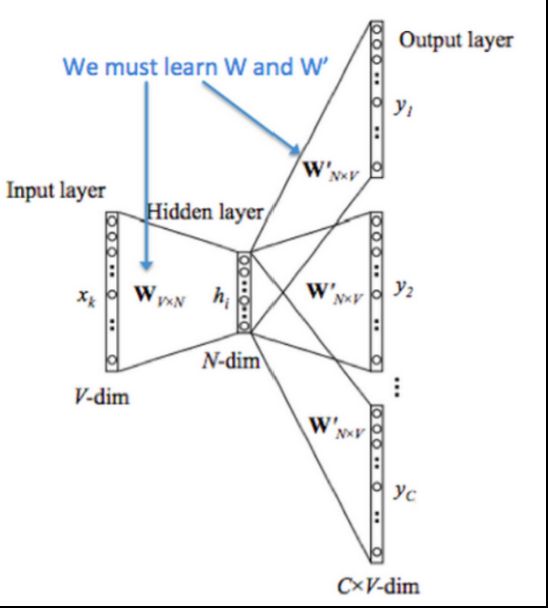
输入:一个单词的int表示。假设词表大小为N。
projection:将单词映射为一个词向量,维度是embedding_size.这里会产生一个形状为Nxembedding_size 的参数W。这个参数就是本次任务最重要的输出。作为词向量,提供给下游。
output:将这个词向量做线性变化后,得到在每个单词上的概率。希望在周围词上的概率最大。
目标函数:找到在给定 w t w_t wt的情况下 w t + j w_{t+j} wt+j出现的概率: p ( w t + j ∣ w t ) p(w_{t+j}|w_t) p(wt+j∣wt),再对这个概率取log。对所有窗口范围内的概率log和取最大值。t是从1到T的,再对这所有和,取和。
具体概率的计算方式是 u o u_o uo是输出的词向量, v c v_c vc是输入词向量。
p ( o ∣ c ) = e x p ( u o T v c ) ∑ w = 1 W e x p ( u w T v c ) p(o|c)=\dfrac{exp(u_o^Tv_c)}{\sum_{w=1}^W exp(u_w^Tv_c)} p(o∣c)=∑w=1Wexp(uwTvc)exp(uoTvc)
c:表示中心词
o:表示周为此
v c v_c vc表示输入词向量
u o u_o uo表示输出词向量
用两个词向量的点积表示o这个单词可能出现的概率: u o ∗ v c u_o*v_c uo∗vc
损失函数:上面的概率越大越好,作为损失函数,就是将该函数取反,求最小值。
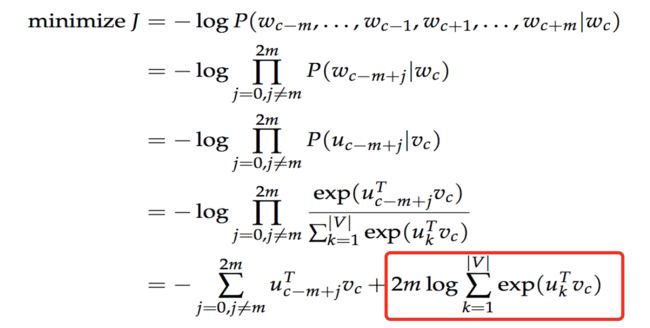
这里最大的问题是p(o|c)的分母是很大的。要计算 v c v_c vc与词库中每一个单词的词向量的和。如果词库有50万个单词,那就要计算50万次。计算量很大。看损失函数的最后一项,也是一样的。
可以采取的措施是负例采样。
我们的输入input embeding是一个50万x100维的矩阵。(假设我们用100维的向量表示一个词)。输出output embedding是一个50万x100维的矩阵。
我们把任务换一个角度。对于 w t w_t wt不要计算周围单词在整个词库上的概率。我们将词库的单词分为周围单词和非周围单词两类。这样就把一个50万分类问题变为2分类问题。如果单词 u k u_k uk是 w t w_t wt的周围单词,那就概率高一些。否则概率低一些。

用周为词向量点乘中心词向量,对结果做sigmoid,表示w是c的周围词的概率。对于需要连续计算m个周围词的概率的乘积,可以转为对概率求log和。因此出现了上面的公式。
我们希望目标函数越大越好。
对于负例我们从词库中采样一部分单词即可。采样后的概率做了一下变换才参与到计算中。
最后对我们有用的数据是输入的embedding,这是词的稠密向量。可以很好的表示词之间的相关性。
最后模型代码实现。
class EmbeddingModel(nn.Module):
def __init__(self, vocab_size, embed_size):
super(EmbeddingModel, self).__init__()
self.vocab_size = vocab_size
self.embed_size = embed_size
initrange = 0.5 / self.embed_size
self.out_embed = nn.Embedding(self.vocab_size, self.embed_size, sparse=False)
self.out_embed.weight.data.uniform_(-initrange, initrange)
self.in_embed = nn.Embedding(self.vocab_size, self.embed_size, sparse=False)
self.in_embed.weight.data.uniform_(-initrange, initrange)
def forward(self, input_labels, pos_labels, neg_labels):
# input_labels:[batch_size]
# pos_labels:[batch_size, c-1]
# neg_labels:[batch_size, (c-1)*K]
batch_size = input_labels.size(0)
input_embedding = self.in_embed(input_labels) # [batch_size,embedding_size]
pos_embedding = self.out_embed(pos_labels) # [batch_size,c*2-1,embedding_size]
neg_embedding = self.out_embed(neg_labels) # [batch_size,(c*2-1)*K,embedding_size]
input_embedding = input_embedding.unsqueeze(2) # [batch_size,embedding_size,1]
# bmm((b×n×m), (b x m x p)) = (b x n x p)
pos_dot = torch.bmm(pos_embedding, input_embedding) # [batch_size,c*2-1,1]
neg_dot = torch.bmm(neg_embedding, -input_embedding)
pos_dot = pos_dot.squeeze() # [batch_size,c*2-1]
neg_dot = neg_dot.squeeze() # [batch_size,(c*2-1)*K]
log_pos = F.logsigmoid(pos_dot).sum(1) # [batch_size]
log_neg = F.logsigmoid(neg_dot).sum(1) # [batch_size]
loss = log_pos + log_neg
# 因为希望概率越大越好,所以损失就是越小越好,所以加负号。
return -loss
def input_embeddings(self):
return self.in_embed.weight.data.cpu().numpy()