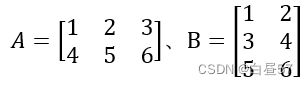国防科大:问题求解——函数运用
第1关:天数计算
任务描述
实现dayOfYear(y,m,d)函数,该函数的功能是计算y年m月d日是该年的第几天。
相关知识
天数其实就等于之前月份的总天数,再加上d。所以,可以将“计算某年某月包含的天数”定义为一个函数,再在dayOfYear函数中调用这个函数,问题就变得简单了。 而“计算某年某月包含的天数”这个问题的关键是计算 2 月的天数,因为除 2 月外,其它月份的天数都是固定的。所以在解决“计算某年某月包含的天数”问题之前,要先解决“计算 2 月天数”的问题,方法如下(详见“问题求解——分支”实训第 8 关)。
2 月有多少天与当年是否为闰年有关: ● 闰年的 2 月有 29 天; ● 非闰年的 2 月有 28 天。 闰年又分以下两种(即通常所说的:四年一闰,百年不闰,四百年再闰): ● 普通闰年:年份是 4 的倍数,且不是 100 的倍数; ● 世纪闰年:年份是 400 的倍数。
综上,解决本问题可以采用如下过程: 1)定义一个函数,计算某年 2 月包含的天数; 2)定义一个函数,计算某年某月包含的天数; 3)定义dayOfYear函数,计算某年某月某日是这年第几天。
编程要求
在 Begin-End 区间实现dayOfYear函数,具体要求见上。
测试说明
在每个测试集中,系统会给定年月日(分别用变量y、m、d表示),例如,测试集 1 的输入是:
20201024
程序的功能是计算y年m月d日是该年的第几天,例如,测试集 1 的运行结果为:
2020年10月24日是这年第298天
开始你的任务吧,祝你成功!
代码:
########## Begin ##########
M = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]
def dayOfYear(y, m, d):
if y%400==0 or (y%100!=0 and y%4==0):
M[1]+=1
sum=0
for i in range(m-1):
sum+=M[i]
return sum+d
########## End ##########
y = int(input()) #年
m = int(input()) #月
d = int(input()) #日
day = dayOfYear(y,m,d)
print('%d年%d月%d日是这年第%d天' % (y,m,d,day))第2关:打印圣诞树
任务描述
本关任务是用print函数打印一颗圣诞树,如下所示:
************************************************************************************************************************************************************************************************
说明如下: 1)每行都是 19 个字符,由*和空格组成,如第 3 行是:7 个空格、5 个*、7 个空格; 2)圣诞树的对称轴在 19 个字符的正中间,即第 10 个字符处,也就是说,在每一行中,第 10 个字符是*,而第 1~9 个字符与第 11~19 个字符顺序相反; 3)3 个三角形的总行数分别为 5、7、10,在每个三角形中,从上往下数第 i 行(i 从 0 开始)中*的数量为 2∗i+1; 4)最下面的矩形共 6 行,每行3个*。
相关知识
提示:可以将“打印圣诞树”的问题分解成“打印三角形”和“打印矩形”这两个小问题,而这两个小问题又可以进一步分解成“打印一行”这个基本问题。所以,先思考如何打印一行,在此基础上实现打印三角形和矩形的功能,最终打印出整个圣诞树。 其他知识参考“问题求解——for 循环”实训第 1 关。
编程要求
在 Begin-End 区间编写程序,打印圣诞树,具体要求见上。
测试说明
程序运行结果为:
************************************************************************************************************************************************************************************************
开始你的任务吧,祝你成功!
代码:
########## Begin ##########
def Output(x):
y=int((19-x)/2)
print(' '*y,'*'*x,' '*y,sep='')
l=[5,7,9]
for i in l:
for j in range(i):
Output(j*2+1)
for i in range(6):
Output(3)
########## End ##########第3关:矩阵乘法
任务描述
背景
设 A 是 m 行 p 列矩阵、B 是 p 行 n 列矩阵,则 A 与 B 可以相乘,将结果记为 C,C 是一个 m 行 n 列的矩阵。若 A、B、C 中第 i 行第 j 列元素分别记为 ai,j、bi,j、ci,j,则有:
也就是说,C 的第 i 行第 j 列元素是 A 中第 i 行与 B 中第 j 列对应元素的乘积之和。例如:
则:
例如,C 的第 1 行第 2 列元素 c1,2 的计算过程是:A 第 1 行是 [1,2,3],B 的第 2 列是 [2,4,6],则 c1,2=1×2+2×4+3×6=28。
任务
本关任务是实现multiply(A, B)函数,说明如下: 1)参数A和B是嵌套列表,分别对应前面的矩阵 A 和 B; 2)函数返回值也是嵌套列表,对应矩阵 A 和 B 相乘的结果。
相关知识
提示:可以将该问题分解成“定义零矩阵”、“求一个 ci,j”和“求所有 ci,j”这三个小问题,分别定义为三个函数。 其他知识参考“问题求解——嵌套列表”实训第 2 关。
编程要求
在 Begin-End 区间实现multiply函数,具体要求见上。
测试说明
在每个测试集中,系统会给定两个整数num1和num2,分别用于生成矩阵 A 和矩阵 B,例如,测试集 1 的输入是:
01
测试集的运行结果是先打印矩阵 A 和矩阵 B(利用num1和num2生成的矩阵),再打印 A×B 的结果,例如,测试集 1 的运行结果为:
A=1 2 34 5 6B=1 23 45 6C=AxB=22 2849 64
开始你的任务吧,祝你成功!
代码:
########## Begin ##########
def multiply(A, B) :
n, m, p = len(A), len(A[0]), len(B[0])
C = []
for i in range(n) :
sum = [0] * p
C.append(sum)
for i in range(n) :
for j in range(p) :
for k in range(m) :
C[i][j] += A[i][k] * B[k][j]
return C
########## End ##########
import myMatrix
num1 = int(input())
num2 = int(input())
A = myMatrix.getMatrix(num1)
print('A=')
myMatrix.printMatrix(A)
B = myMatrix.getMatrix(num2)
print('\nB=')
myMatrix.printMatrix(B)
C=multiply(A, B)
print('\nC=AxB=')
myMatrix.printMatrix(C)第5关:实现欧拉函数
任务描述
欧拉函数是数论中一个非常重要的函数。 在给出欧拉函数之前,先要了解互素的概念。所谓两个数互素,是指这两个数的最大公约数为 1,如 10 和 3 的最大公约数为 1,则 10 和 3 互素。 在此基础上定义欧拉函数 Φ(n):对于一个正整数 n,Φ(n) 的值是小于等于 n 且与 n 互素的正整数的个数。例如,与 10 互素的正整数有 1、3、7、9,共 4 个,所以 Φ(10)=4。此外,规定 Φ(1)=1。 本关任务就是实现函数Phi(n),其功能是计算正整数n对应的欧拉函数值。
相关知识
参考之前关卡。
编程要求
在 Begin-End 区间实现Phi函数,具体要求见上。
测试说明
在每个测试集中,系统会给定一个正整数 n(用变量n表示),例如,测试集 1 的输入是:
10
程序的功能是计算 n 对应的欧拉函数值,例如,测试集 1 的运行结果为:
Phi(10)=4
开始你的任务吧,祝你成功!
代码:
########## Begin ##########
def Gcd(x, y) :
if x % y == 0 :
return y
return Gcd(y, x % y)
def Phi(x) :
mdl = 0
for i in range(1, x) :
if Gcd(i, x) == 1 :
mdl += 1
return mdl
########## End ##########
n=int(input(''))
print('Phi(%d)=%d' % (n, Phi(n)))
第6关:推翻欧拉的猜想
任务描述
一直以来,人们非常希望能够找到一个关于素数的通项公式,利用公式可以生成所有素数。但遗憾的是,绝大部分公式都已经被证明是不正确的,欧拉素数公式就是其中一个。 欧拉素数公式形式为 f(n)=n2+n+41。例如,f(1)=43、f(2)=47、f(3)=53 等都是素数。在手工计算年代,人们难以计算很大的数,所以认为该公式生成的都是素数。而利用现代计算机等工具,则很容易证明该假设并不成立。 本关任务就是推翻“欧拉素数公式生成的都是素数”这一假设。
相关知识
参考之前关卡。
编程要求
在 Begin-End 区间编写程序,证明欧拉素数公式生成的并不都是素数,要求如下: 1)程序总共打印 m 行,每行对应一个 f(n),n 依次为 1 到 m; 2)前 m-1 行是假设成立的情况,例如,第 1 行打印(标红字样为打印内容,中间无空格):f(1)=43是素数 ; 3)最后一行是假设首次不成立的情况,例如,如果 f(1500) 是欧拉素数公式生成的首个非素数(实际上不是首个),则最后一行打印(标红字样为打印内容,中间无空格):f(1500)=2251541=83*27127不是素数 ,其中,83*27127中的83是2251541的最小约数(除 1 外)。
测试说明
程序运行结果为:
f(1)=43是素数f(2)=47是素数f(3)=53是素数f(4)=61是素数f(5)=71是素数f(6)=83是素数f(7)=97是素数f(8)=113是素数f(9)=131是素数f(10)=151是素数……
开始你的任务吧,祝你成功!
代码:
########## Begin ##########
def f(x) :
return x * x + x + 41
def is_prime(x) :
if x == 2 :
return True
for i in range(2, x) :
if x % i == 0 :
return False
return True
def mindiv(x) :
for i in range(2, x) :
if x % i == 0 :
return i, x / i
return 1, x
i = 1
while is_prime(f(i)) :
print('f(%d)=%d是素数' % (i, f(i)))
i = i + 1
x, y = mindiv(f(i))
print('f(%d)=%d=%d*%d不是素数' %(i, f(i), x, y))
########## End ##########