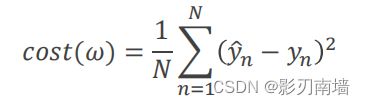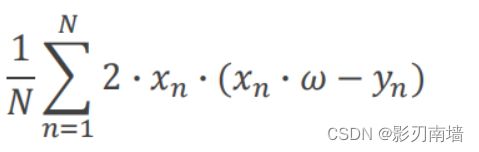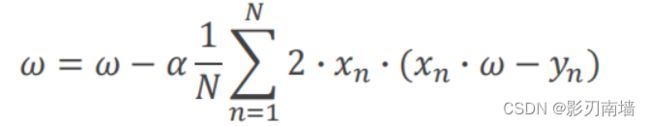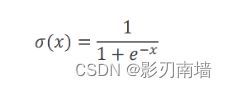深度学习基础入门笔记集合

学习视频bilibili链接： 河北工业大学人工智能与数据科学学院教师 刘洪普

第一讲 Overview 4/18

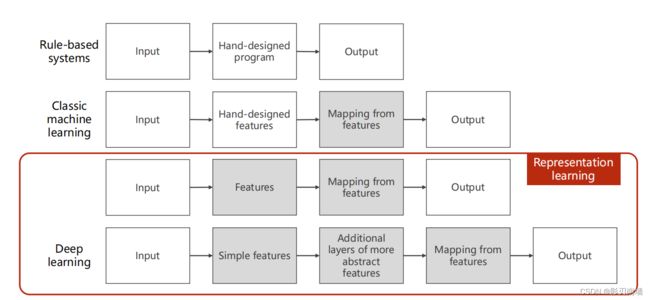
1.深度学习关系图 人工智能、机器学习【分类、聚类、回归、降维】、表示学习、深度学习

2.深度学习需要用到哪些知识储备/工具？ 线性代数+概率论+python

3.深度学习框架 PyTorch(学术界，facebook研发)vs TensorFlow(工业界，google研发)

4.pytorch优点：动态图更灵活、易于调试、代码简便

【深度学习：具体->抽象 提取特征、映射特征、CUDA、降维（维度灾难）】

5.挑战：人工设计特征的局限、SVM（支持向量机）难以处理大量数据、越来越多的非结构化数据

6.机器学习的算法和平常算法不一样，机器学习的算法来自于数据，从数据中提炼模型，训练，测试，形成算法。大部分机器学习算法是监督学习，就是知道结果，打了标签的。

7.寒武纪物种大爆发【因为进化出了眼睛】

哺乳动物的视觉神经是分层的，较低的层次处理简单信息，较高的层次处理高级信息，神经网络的生物学来源。

第二讲 线性模型【穷举】4/19

线性模型
$$y^{\prime }=wx+b$$
非线性模型，如二元一次函数
$$y=a{x}^2+bx+c$$
损失函数计算，损失函数用方差
$$loss=(y^{\prime }-y{)}^2=(x\ast w-y{)}^2$$
均方误差最小

1.线性模型是最简单的模型，通过估计参数，找到最优参数值，使得均方误差最小。

2.训练集、开发集（验证集，方法有随机验证、交叉验证）、测试集，开发集从训练集中分离出，用来验证预测效果，如果预测效果好的话，再将测试集和开发集一起训练，得出更接近真实值的模型参数。

3.python实现

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

#定义模型
def forward(x):
    return x * w

#损失函数
def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)

w_list = []#参数列表
mse_list = []#均方误差列表
#随机生成w 基于穷举法
for w in np.arange(0.0,4.1,0.1):
    print("w=",w)
    l_sum = 0#总损失值
    for x_val,y_val in zip(x_data,y_data):
        y_pred_val = forward(x_val)#预测值
        loss_val = loss(x_val,y_val)#损失
        l_sum +=loss_val#累加求和
        print('\t',x_val,y_val,y_pred_val,loss_val)
    print('MSE=',l_sum/3)
    w_list.append(w)
    mse_list.append(l_sum/3)

#绘制图形，找到最优参数
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

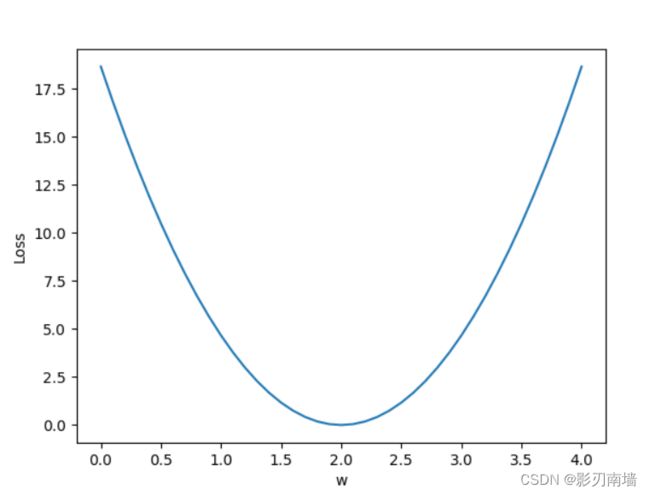
运行结果，可以知道当权重为2.0时损失函数取得最小值为0.0

代码感悟：

zip(list a ,list b)函数 #打包成元组列表

res = np.arange(0.0,4.1,0.1)
等价于
res = [i/10 for i in range(0,41,1)]#range(start,end,step)三个参数都必须为integer、

变量w定义赋值在后面，作用在全局（前面也可以），即作用于为全局，而函数却不可以，先定义再引用

第三讲 梯度下降算法【贪心】4/19

1.梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

2.梯度 = / ，求偏导

3.迭代公式，更新 = − / （其中为学习率，一般在0.01~0.1之间，为参数，也叫权重）

4.梯度下降就是沿着梯度下降（为负）的方向去更新的值，基于贪心思想【寻找当前最优】，一般都能找到局部最优解，但不一定是全局最优。必要条件，loss()是凸函数

损失函数：方差 () =

梯度 损失函数对权重求导 / =

迭代公式更新权重 a为学习率

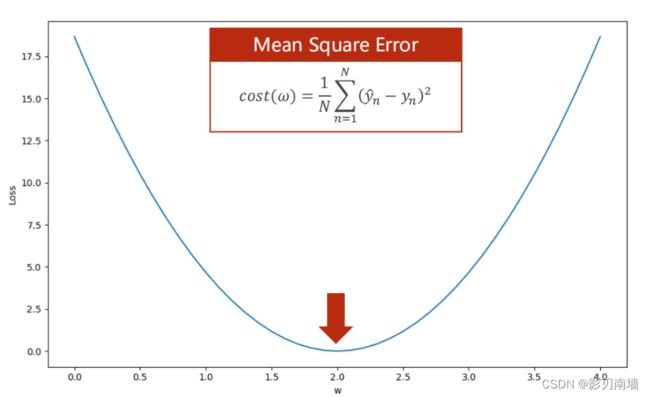
4-2寻找cost最小值，第一种是观察法，如下图可知权重为2.0时损失函数取得最小值0.0

5.第二种是寻找到导数（梯度）为0的点，极值点（局部最值），由于（初试导数值为正）我们是沿着导数减小的方向接近0【或者初始导数值为负，沿着导数增大的方向接近0】，所以该导数为0点是极小值点，也就是局部最小值点，即局部最优点。

​ 传统的梯度下降算法更新 是存在前后依赖关系的，所以时间复杂度会降低，因为总是在上一个 的基础上朝着最优点的方向前进，但是存在一种致命缺点，鞍点，这种点（平行，导数为0）会使得梯度下降失效，因为到了此点附近梯度为0，不会更新了，但该点又不是局部最优。

​ 改进的随机梯度下降算法，通过一个随机干扰，可以有效解决这个办法，提升算法的性能（鲁棒性）。但与此同时，随机梯度的mini-batch会使得时间复杂度上升。

5-2 随机梯度利用单个样本点对权重进行更新

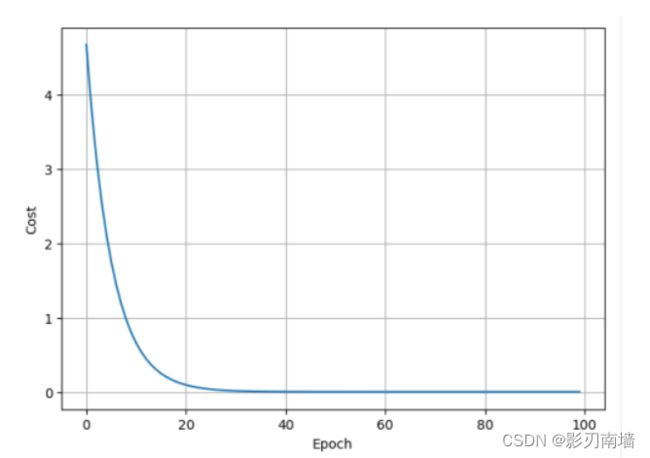
6.下图展示理想情况下，均方误差随迭代次数的变化，可以看到先是快速下降后平缓下降，直至收敛

改进的python代码实现

#coding=utf-8
import matplotlib.pyplot as plt

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,8.0]

w = 1.0#初始化权重为1.0

#线性模型，前馈
def forward(x):
    return x * w
#均方误差计算，前馈
def cost(xs,ys):
    cost = 0#误差
    for x,y in zip(xs,ys):
        y_pred = forward(x)#预测值
        cost += (y_pred - y) ** 2#累加方差求和
        return cost / len(xs)#求均方误差

#计算所有样本的平均梯度，后馈计算梯度，更新权重
def gradient(xs,ys):
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2 * x * (x * w - y)#梯度计算,导数，还要除以N 
    return grad / len(xs)#返回a* /

epoch_list = []
cost_val_list = []
print('Predict (before training)',4,forward(4))
for epoch in range(100):#迭代更新100轮
    cost_val = cost(x_data,y_data)#误差
    grad_val = gradient(x_data,y_data)#梯度
    w -= 0.01*grad_val#迭代更新权重，学习率为0.01
    print('Epoch:', epoch,'w=',w,'loss=',cost_val)
    epoch_list.append(epoch)
    cost_val_list.append(cost_val)

plt.plot(epoch_list,cost_val_list)
plt.xlabel('Epoch')
plt.ylabel('Cost')
plt.show()
print('Predict (after training)',4,forward(4))

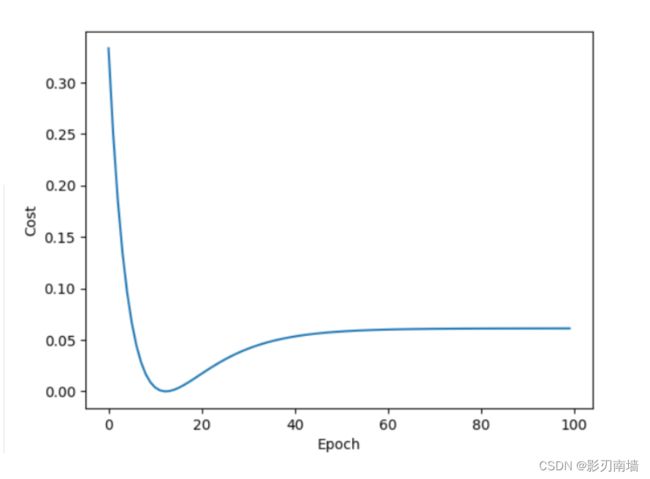
误差随迭代次数变化情况，可以看到，过拟合了，可能是因为数据量过小，训练次数【epoch=100】较多导致，针对这种情况，我们可以保存参数，并再每次训练完毕后及时更新是的损失函数最小的参数值，最后得到的是预测效果最好的参数。

【权重共更新了100次】

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
    return x * w
#单个样本点损失函数
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2
#单个样本点梯度计算
def gradient(x, y):
    return 2 * x * (x * w - y)

print('Predict (before training)', 4, forward(4))

loss_list = []
epoch_list = []
#每次更新权重都只用到单个样本
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        grad = gradient(x, y)
        w = w - 0.01 * grad
        print("\tgrad: ", x, y, grad)
        l = loss(x, y)
        loss_list.append(l)
        epoch_list.append(epoch)

    print("progress:", epoch, "w=", w, "loss=", l)
print('Predict (after training)', 4, forward(4))
plt.plot(epoch_list, loss_list)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()

此时batch_size=1，由于每次都只使用单个样本来更新权重，无法运用到GPU处理矩阵运算的并行优势了，因此时间复杂度大，时间上性能较差。

优化方案，batch_size的值适当取大一点，这样可以结合随机和非随机的优势，做到折中，使得训练效果比较好。【时间和性能上都比较好】

再来看看随机梯度下降算法的训练效果，loss逐渐收敛【权重共更新了300次】

第四讲 反向传播【神经网络、弹性】4/20

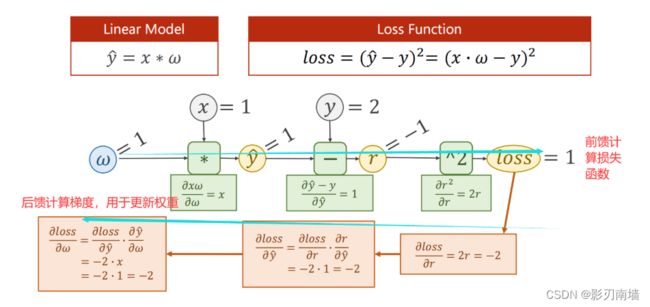
1.反向传播/前向传播【反馈/前馈】：前馈计算值loss，反馈计算梯度如 /

2.为什么双层神经网络要加入非线性函数【激活函数】？

目的是复杂化神经网络，让它无法化简，如果作的都是线性变换，无论有多少层都可以化简为一层，那加这么多权重就没有意义了。

3.神经网络要运用到复合函数链式求导法则，因为每一层都是一个最简单的计算，比如加法或者乘法。

4.pytorch实现神经网络？

4-1基本数据结构：tensor张量是一个类，包含data和grad，即权重和梯度。

4-2为什么要释放计算图？因为下一次图可能更新了,每进行一次反向传播都要释放计算图，这种方式比较灵活，这也是pytorch的核心竞争力之一。

tensor包含的data和grad,grad也是一个tensor，如果权重更新时使用的是张量【tensor】而不是值会导致计算图堆叠（因为一个tensor有一个计算图），导致内存爆炸。

5.神经网络的矩阵计算?

输入5个X，中间节点6个，权重需要30个 X[1 * 5] * w[5 * 6] = s[1 * 6]

6.完整推导过程

7.训练代码

#coding=utf-8
import torch

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = torch.Tensor([1.0])#权重w初始化为1.0
w.requires_grad = True#需要梯度

#预测值
def forward(x):
    return w * x

#损失函数
def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

print("Predict (before training)",4,forward(4).item())

#随机梯度，用每一个样本来更新梯度
for epoch in range(100):
    for x,y in zip(x_data, y_data):
        l = loss(x,y)#前馈计算损失函数
        l.backward()#后馈计算梯度
        #w.grad.item()是标量，w.grad.data是张量
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data#用梯度更新权重

        w.grad.data.zero_()#梯度显示清零

    print("progress:", epoch, l.item())

print("Predict (after training)", 4, forward(4))

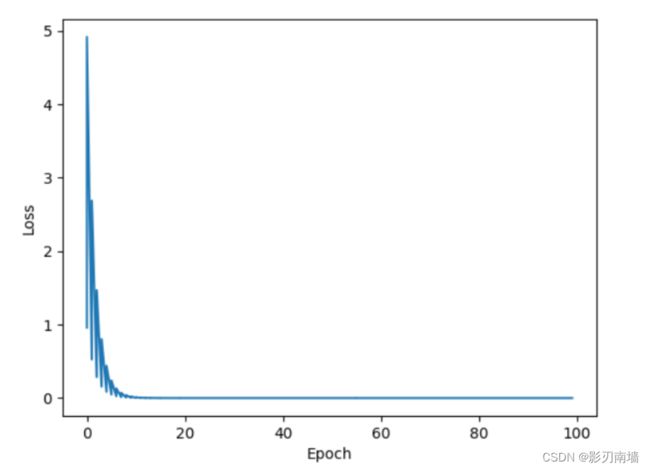
7-2 训练结果【在收敛的过程中发现有明显的抖动】

第五讲 用PyTorch实现线性回归 4/21

1.pytorch的linearmodel类有哪些成员（变量/方法）?

init(self)；forward(self, x)；

2.weight and bias【分别对应线性模型 = ∗ + b的（权重）和b（偏置）】

3.优化器是什么，有什么作用？请比较使用不同优化器的效果【在最后】

优化器实现了随机梯度下降算法，梯度公式（链式求导）不需要我们求了。

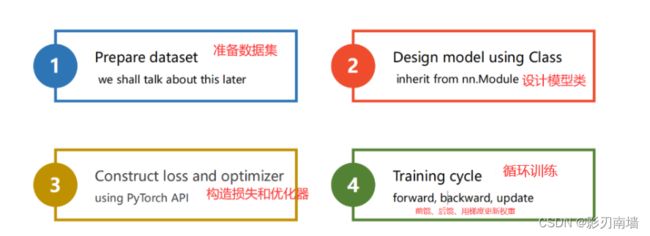
4.用linearmodel优化大致的步骤有哪些？

5.为什么要用到矩阵运算，有什么好处？ 【代码上】减少显示使用for循环，【性能上】提高运算效率。

6-1python代码实现

#coding=utf-8
import torch
import matplotlib.pyplot as plt

#①准备数据集
x_data = torch.Tensor([[1.0],[2.0],[3.0]])#3*1的矩阵
y_data = torch.Tensor([[2.0],[4.0],[6.0]])#3*1的矩阵

#②定义模型类
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel,self).__init__()#调用父类__init__()函数
        self.linear = torch.nn.Linear(1,1)#输入和输出都是一维

    def forward(self,x):#前馈函数
        y_pred = self.linear(x)
        return y_pred

model = LinearModel()#实例化线性模型类

#3定义损失函数和优化器
criterion = torch.nn.MSELoss(size_average=False)#定义损失函数，false表示不需要设置batch_size
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)#定义SGD优化器,学习率学0.01

epoch_list = []
loss_list = []

#④循环训练
for epoch in range(100):#迭代100次
    y_pred = model(x_data)#预测值
    loss = criterion(y_pred,y_data)#损失
    # print(epoch, loss.item())
    epoch_list.append(epoch)
    loss_list.append(loss.item())

    optimizer.zero_grad()#梯度清零
    loss.backward()#后馈
    optimizer.step()#更新权重【随机梯度下降算法】
    print('w = ', model.linear.weight.item())
    print('b = ',model.linear.bias.item())

print(epoch, loss.item())

#测试
x_test = torch.Tensor([[4.0]])#测试集
y_test = model(x_test)#预测值
print('y_pred = ', y_test.data)#data和.item()有什么区别

#画图
plt.plot(epoch_list,loss_list)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()

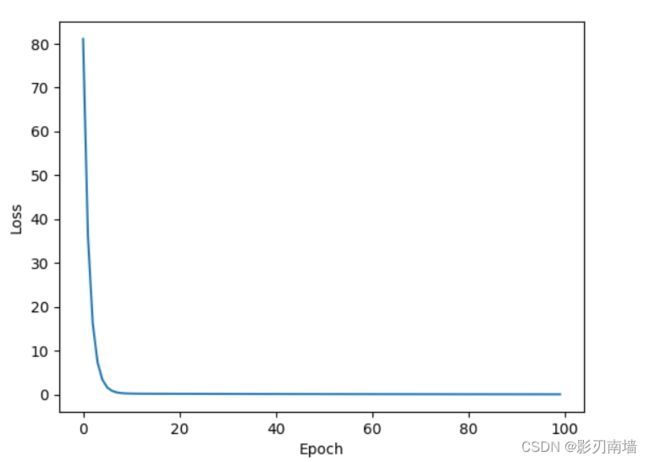
6-2训练效果【迭代100次】

6-3训练100次vs训练1000次的误差

6-4比较不同优化器训练100次效果loss,可以看出Rprop优化器性能最好。

迭代器	loss
SGD	0.021307483315467834
Adam	32.71455383300781
Adamax	8.656513214111328
Adagrad	50.21343994140625
ASGD	0.05351773649454117
RMSprop	3.2769417762756348
Rprop	1.404339968757995e-07

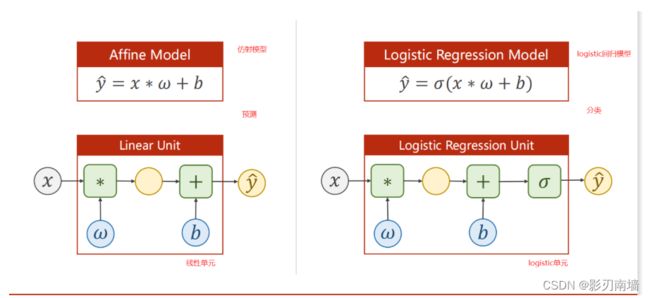
第六讲 逻辑斯蒂回归二分类【logistic regression】 4/22

1.逻辑斯蒂回归计算图有什么变化？

2.损失函数的选取

3.分类和预测问题有什么异同？预测得到的是一个确定的值，而分类得到的是每种情况的概率，概率和为1，概率最大的一般就是预测出来的分类，分类是一种概率分布。

4.sigmoid函数？

Sigmoid函数是一种具有S形曲线的数学函数。Sigmoid函数是一种激活函数，并且更具体地定义为挤压函数（squashing function)。压缩函数将输出限制在0到1之间，从而使这些函数在概率预测中非常有用。

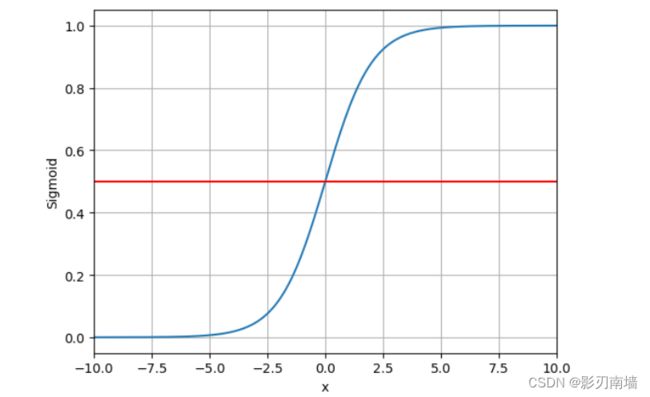
5.logistic 函数 解析式及图像，从图中可知(-∞)=0，(0)=0.5，(+∞)=1

6.size_average=False表示不计算batch大小，也就是不除以N

7.python代码实现

#coding=utf-8
import torch.nn
import torch.nn.functional as F
import torch
import numpy as np
import matplotlib.pyplot as plt

#准备数据
x_data = torch.Tensor([[1.0,],[2.0],[3.0]])#数据的意义是学习时长
y_data = torch.Tensor([[0],[0],[1]])#分类模型，0表示不能通过考试，1表示能通过考试

#定义模型
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1,1)#输入输出都是一维

    def forward(self,x):
        y_pred = F.sigmoid(self.linear(x))#激活函数预测二分类
        return y_pred
    
model = LogisticRegressionModel()#实例化模型类

#构造损失函数和优化器
criterion = torch.nn.BCELoss(size_average=False)#损失函数BCE
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)#SGD优化器，学习率0.01

epoch_list = []
loss_list = []

#循环训练
for epoch in range(100000):
    y_pred = model(x_data)#预测
    loss = criterion(y_pred, y_data)#计算损失
    epoch_list.append(epoch)
    loss_list.append(loss.item())

    optimizer.zero_grad()#清零
    loss.backward()#后馈
    optimizer.step()#更新

# plt.plot(epoch_list,loss_list)
# plt.xlabel('Epoch')
# plt.ylabel('Loss')
# plt.show()

#测试
x = np.linspace(0,10,200)#[0,,,10]200等份
x_t = torch.Tensor(x).view((200,1))#改变张量形状【200，1】
y_t = model(x_t)
y = y_t.data.numpy()#把data转成数组
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')#画一条红色分界线
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()#网格
plt.show()

7-2训练10W次效果，loss函数

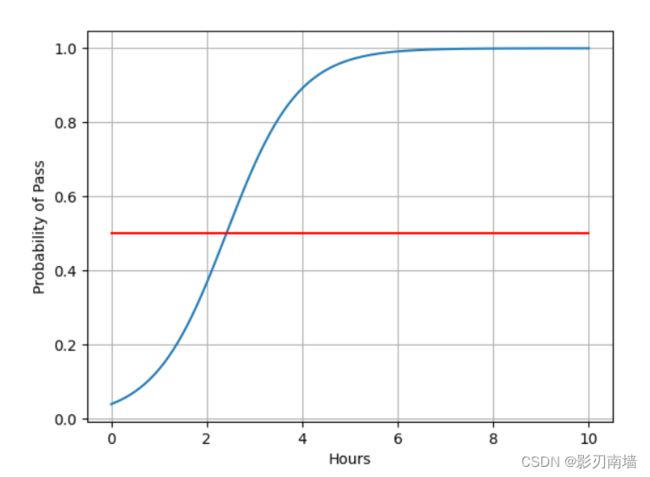
7-3训练1000次，预测效果，可以看到大概在2.5小时左右通过几率为50%，大于2.5小时学习时间预测会通过考试，小于则预测不能通过。

第七讲 处理多维特征的输入 4/23 --5.14

**神经网络的本质（映射）？**非线性空间变换函数层数越多，学习能力越强，当超过一定阈值时，会把噪声的特征也学习到，反而不好。【泛化和拟合】

**矩阵的本质？**矩阵是一个空间变换的函数，N维空间映射到M维空间。

激活函数（RElu、sigmoid)，做非线性变换，避免多层神经网络简化为一层，降低性能。

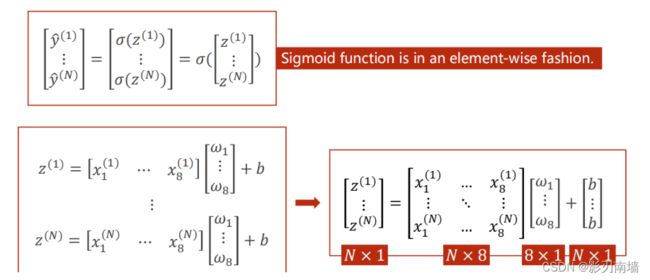
多特征输入矩阵是怎么实现的

矩阵和for循环的比较，GPU更易于处理矩阵运算[matrix cookbook,里面有介绍矩阵求导]，矩阵运算能利用GPU并行特性，比for高效。

python代码实现

#coding=utf-8
import torch
import numpy as np
import matplotlib.pyplot as plt

#准备数据集,759条,前面的用来训练，最后50条用来测试
xy = np.loadtxt('../data/diabetes.csv.gz', delimiter=',', dtype=np.float32)#加载数据
x_data = torch.from_numpy(xy[:-50,:-1])#输入，8个特征值数据
y_data = torch.from_numpy(xy[:-50,[-1]])#输出，0-1分类
x_test = torch.from_numpy(xy[-50:,:-1])
y_test = torch.from_numpy(xy[-50:,[-1]])
# print(len(x_data))

#定义模型
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        #三层的神经网络
        self.linear1 = torch.nn.Linear(8, 6)#8个特征值映射成6个输出
        self.linear2 = torch.nn.Linear(6, 4)#6->4
        self.linear3 = torch.nn.Linear(4, 1)#4->1
        self.sigmoid = torch.nn.Sigmoid()#激活函数

    def forward(self,x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model()

#定义损失函数和优化器
criterion = torch.nn.BCELoss(size_average=True)

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)#学习率0.1

epoch_list = []
loss_list = []
#循环训练
for epoch in range(100):
    #前馈
    y_pred = model(x_data)#未使用mini-batch
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    #后馈
    optimizer.zero_grad()
    loss.backward()

    #更新
    optimizer.step()
    epoch_list.append(epoch)
    loss_list.append(loss)

#绘图
plt.plot(epoch_list, loss_list)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()

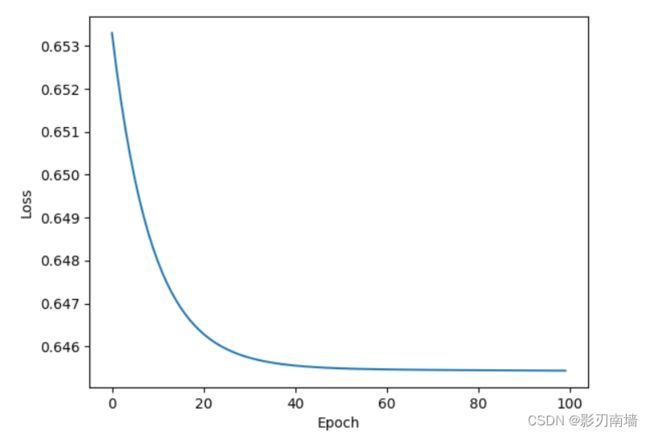
训练100轮效果

第八讲 加载数据集 4/24

1.**dataset和dataloader? **dataset是一个抽象类，必须继承才能实例化，作用是定义数据集；dataloader是一个工具类，可以直接使用，用来帮助我们加载数据集。dataloader将（大）数据集从外存读入内存，内存中放不下，分批加载。

2.三个概念（epoch、batch-size、lteration）

epoch:所有训练例子中有一次前向传播和一次反向传播。

batch-size:一次前馈后馈中的训练实例数。

Iteration:传递的次数，使用[批处理大小]的每一次传递示例数。

3.shuffle:洗牌，打乱顺序，随机组合

4.全部batch、mini-batch和梯度下降、随机梯度下降的关系（视频开头）

随机梯度只用一个样本，优点是克服鞍点，取得更好性能。梯度下降用全部数据，优势是用到了CPU/GPU并行特性，（时间上）速度快，mini-batch则是一个折中方案。

5.num_worker参数 创建多线程，提前加载未来 会用到的batch数据

6.magic function:魔法函数 ，类的保留方法

sigmoid函数优势 相比RUle函数而言， 可以使用 sigmoid或者softmax归一化 处理一下数据，使得输入数据分布在0-1之间。

7.python代码实现

#coding=utf-8

import torch
from torch.utils.data import Dataset#数据类
from torch.utils.data import DataLoader#加载数据类
import numpy as np
import sys  # 导入sys模块
import matplotlib.pyplot as plt


#准备数据
class DiabetesDataset(Dataset):#继承抽象类Dataset
    def __init__(self, filepath):#初始化
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:,:-1])#输入
        self.y_data = torch.from_numpy(xy[:,[-1]])#标签

    def __getitem__(self, index):#提取数据
        return self.x_data[index],self.y_data[index]

    def __len__(self):#返回数据集长度
        return self.len


#定义模型
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)#8个特征值映射成6个输出
        self.linear2 = torch.nn.Linear(6, 4)#6->4
        self.linear3 = torch.nn.Linear(4, 1)#4->1
        self.sigmoid = torch.nn.Sigmoid()#激活函数,sigmoid函数可以归一化，使得输入值在0-1之间
        # self.activate = torch.nn.ReLU()

    def forward(self,x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x


if __name__ == '__main__':
    sys.setrecursionlimit(3000)  # 将默认的递归深度修改为3000
    #准备数据集
    dataset = DiabetesDataset('../data/diabetes.csv.gz')
    train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)#设定加载类的数据集，batch数量，随机洗牌
    #定义模型
    model = Model()

    #定义损失函数和优化器
    criterion = torch.nn.BCELoss(size_average=True)

    optimizer = torch.optim.SGD(model.parameters(), lr=0.1)#学习率0.1

    epoch_list = []
    loss_list = []
    #循环训练
    for epoch in range(100):#训练100轮
        loss_mean = 0
        #i是mini - batch的序号，batch - size = 32，data - size = len = 753, batch_num = len / batch_size = 23
        for i,data in enumerate(train_loader, 0):#？？？一共有23组mini-batch，当前是第i组
            inputs, labels = data#获得输入和标签数据
            y_pred = model(inputs)#预测
            loss = criterion(y_pred, labels)#计算损失
            print(epoch, i, loss.item())#迭代次数、mini-batch序号，损失函数
            loss_mean = loss_mean+loss.item()#求和

            optimizer.zero_grad()#清零
            loss.backward()#反馈

            optimizer.step()#更新

        epoch_list.append(epoch)
        loss_list.append(loss_mean/23.0)

    #绘图
    plt.plot(epoch_list, loss_list)
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.show()

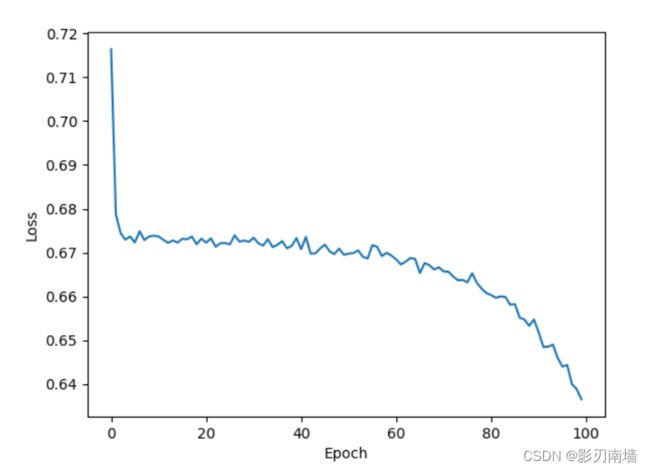
7-2训练100轮loss平均值,可以看到，loss此时还没收敛

第九讲 多分类问题

1.二分类和多分类有什么异同？

二分类只需要计算一个label的概率，然后用１减去该概率便可以得到（属于）另一个分类的的概率；多分类必须把每一个分类的概率独立的计算出来,而且构成一个离散的概率分布，然后选取最大的分类，label设置为1，其他分类label均设置为0。满足以下原则：
（１）所有分类概率均大于０，可以无限接近０（２）所有分类概率之和为１，因此我们选用softmax函数来实现最后一层神经网络，将ｙ＾转变为P｛ｙ＝label｝，softmax层不仅能实现这两点，而且还包含了竞争性。

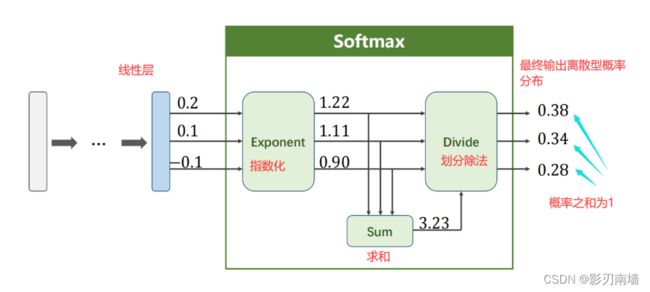
2.softmax层，softmax函数？

softmax层是最后一层神经网络，用来计算每个分类的概率。构造如下，

softmax函数如下,

他可以将Zi∈R映射到(0,1)概率区间,而且分类概率之间能够相互抑制,即拉大高概率,压缩小概率,但不会等于0。

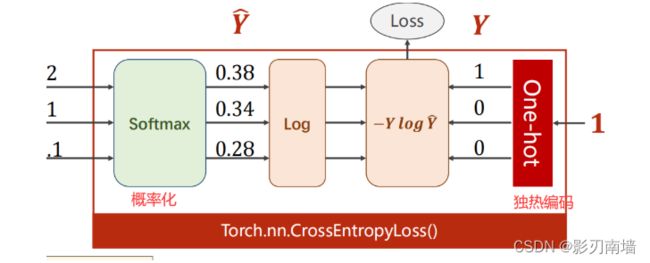
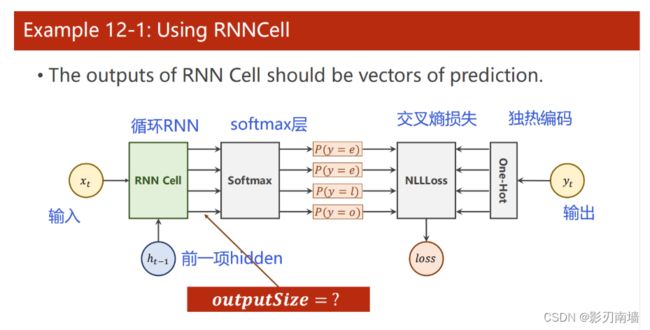
3.loss函数的选取，为什么简化成下式

经过softmax层求得最大概率分类，设其label=1，其他分类label=0，这就是独热编码，然后再跟loss函数进行交叉计算，label=1的时候，y^越大【越接近1】,loss值越小，训练效果越好。其他label=0的分类其loss=0，也没有计算的必要，于是简化了上一节的loss函数。

4.Cross Entropy交叉熵

5.CrossEntropyLoss（交叉熵损失） 、NLLLoss(Negative Log Likelihood Loss,负对数似然损失)

CrossEntropyLoss <==> LogSoftmax + NLLLoss

交叉熵损失包含了softmax层，所以不需要激活函数做非线性变换。如上图，经过softmax层求得最大概率分类，设其label=1，其他分类label=0，这就是独热编码，然后再跟loss函数进行交叉计算，label=1的时候，y^越大【越接近1】,loss值越小，训练效果越好。其他label=0的分类其loss=0，也没有计算的必要，于是简化了上一节的loss函数。

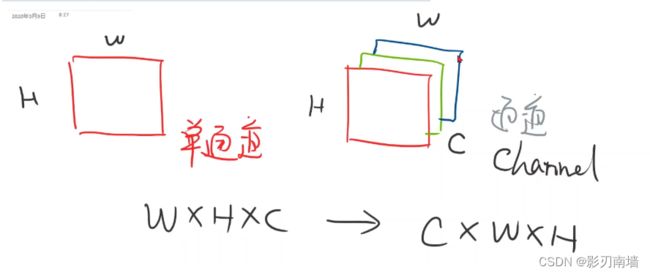
6.PIL【pillow】 CWH[channel通道 width宽度 height高度]

PIL（ Python Imaging Library）是 Python 的第三方图像处理库，由于其功能丰富，API 简洁易用，因此深受好评。 pillow是在 PIL 库的基础上开发的一个支持 Python3 版本的图像处理库，Pillow 不仅是 PIL 库的“复制版”，而且它又在 PIL 库的基础上增加了许多新的特性。Pillow 发展至今，已经成为了比 PIL 更具活力的图像处理库。

6-2补充

独热编码即 One-Hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。 将交叉熵引入计算语言学消岐领域，采用语句的真实语义作为交叉熵的训练集的先验信息，将机器翻译的语义作为测试集后验信息。计算两者的交叉熵，并以交叉熵指导对歧义的辨识和消除。

7.python代码实现

import numpy as np

#softmax+loss numpy
y = np.array([1,0,0])
z = np.array([0.2,0.1,-0.1])
y_pred = np.exp(z) / np.exp(z).sum()
loss = (-y * np.log(y_pred)).sum()
print(loss)

#implements by pytorch
import torch
y = torch.LongTensor([0])#长整型
z = torch.Tensor([[0.2,0.1,-0.1]])
criterion = torch.nn.CrossEntropyLoss()#交叉熵
loss = criterion(z,y)
print(loss.data,loss.item())

#batch-siz=3
criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2,0,1])

Y_pred1 = torch.Tensor([[0.1,0.2,0.9],
                        [1.1,0.1,0.2],
                        [0.2,2.1,0.1]])
Y_pred2 = torch.Tensor([[0.8,0.2,0.9],
                        [0.2,0.3,0.5],
                        [0.2,0.2,0.5]])
l1 = criterion(Y_pred1,Y)
l2 = criterion(Y_pred2,Y)
print('Batch Loss1=',l1.data,'\nBatch Loss2=',l2.data)

#coding=utf-8
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

#准备和加载数据集
batch_size = 64#批大小
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,),(0.3081,))#均值和方差
])
train_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=True,
                               download=True,
                               transform=transform)
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size)

test_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=False,
                               download=True,
                               transform=transform)
test_loader = DataLoader(test_dataset,
                          shuffle=False,
                          batch_size=batch_size)

#定义模型
class Net(torch.nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        #降维处理
        self.l1 = torch.nn.Linear(784,512)
        self.l2 = torch.nn.Linear(512,256)
        self.l3 = torch.nn.Linear(256,128)
        self.l4 = torch.nn.Linear(128,64)
        self.l5 = torch.nn.Linear(64,10)

    def forward(self,x):
        x = x.view(-1,784)
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)#最后一次线性变换层得到的结果做softmax

model = Net()

#构造损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

#定义训练过程
def train(epoch):
    running_loss = 0.0
    for batch_idx,data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()
        #前馈，后馈，更新
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()

        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:#每300轮输出一次
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss /300))

#定义测试过程
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)#max函数
            total += labels.size(0)#
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct / total))

if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

代码运行结果

[1, 300] loss: 2.246
[1, 600] loss: 3.254
[1, 900] loss: 3.666
Accuracy on test set: 89 %
[2, 300] loss: 0.308
[2, 600] loss: 0.575
[2, 900] loss: 0.801
Accuracy on test set: 94 %
[3, 300] loss: 0.182
[3, 600] loss: 0.346
[3, 900] loss: 0.508
Accuracy on test set: 96 %
[4, 300] loss: 0.130
[4, 600] loss: 0.249
[4, 900] loss: 0.370
Accuracy on test set: 96 %
[5, 300] loss: 0.099
[5, 600] loss: 0.193
[5, 900] loss: 0.290
Accuracy on test set: 97 %
[6, 300] loss: 0.074
[6, 600] loss: 0.154
[6, 900] loss: 0.232
Accuracy on test set: 97 %
[7, 300] loss: 0.062
[7, 600] loss: 0.126
[7, 900] loss: 0.190
Accuracy on test set: 97 %
[8, 300] loss: 0.052
[8, 600] loss: 0.101
[8, 900] loss: 0.154
Accuracy on test set: 97 %
[9, 300] loss: 0.043
[9, 600] loss: 0.083
[9, 900] loss: 0.126
Accuracy on test set: 97 %
[10, 300] loss: 0.033
[10, 600] loss: 0.065
[10, 900] loss: 0.104
Accuracy on test set: 97 %

第十讲 卷积神经网络CNN基础篇 5/3

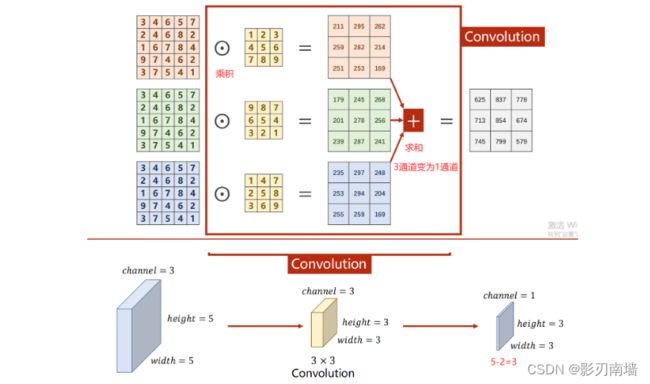
1.什么是卷积？

一种积分，用来平滑函数。

2.卷积核是什么？ 卷积核就是图像处理时，给定输入图像，输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素，其中权值由一个函数定义，这个函数称为卷积核。

3.卷积神经网络和普通神经网络有什么不同？

4.特征提取+分类器 卷积层做特征提取，并且不断降低维数，softmax层做分类器

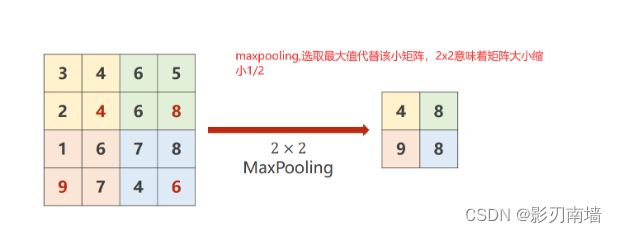
5.池化是什么[pooling]

池化层包含预设定的池化函数，其功能是将特征图中单个点的结果替换为其相邻区域的特征图统计量。 作用是特征选择和信息过滤，由池化大小、步长和填充控制。

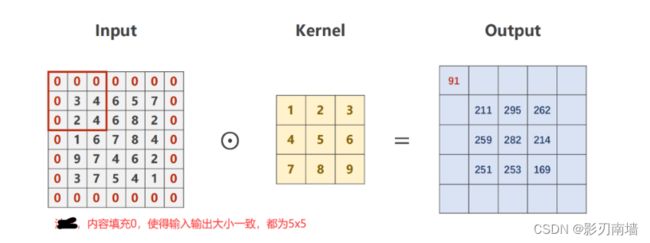
6.padding[填充] 对矩阵进行内容填充使得输出和输入的矩阵大小一致

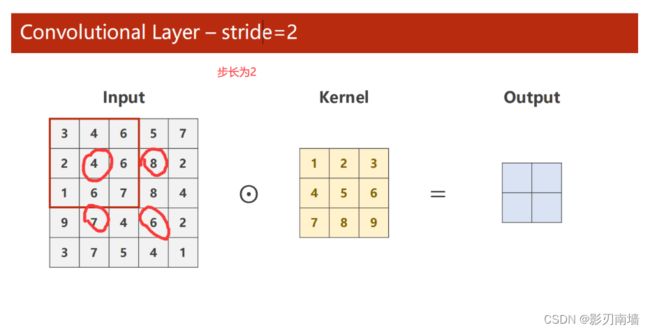
7.stride[步长] 控制卷积的步长，步长越大，信息降维越快，特征提取越快，信息丢失越快

8.怎么使用GPU来做深度学习 参数设置

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") 

model.to(device)

inputs, target = inputs.to(device), target.to(device)

9.模型正确率从97%到98%意味着什么？

模型的识别正确率97%到98%提升了1%，从正确率的角度看似不高；但从错误率角度来看，从3%下降到了2%，下降了1/3，幅度不可谓不小，进步不可谓不小。正是源于使用了更为复杂的神经网络。

10.python代码实现：

#coding=utf-8
import torch
import torch.nn.functional as F
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.optim as optim
import matplotlib.pyplot as plt

#准备和加载数据集
batch_size = 64#批大小
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,),(0.3081,))#均值和方差
])
train_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=True,
                               download=True,
                               transform=transform)
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size)

test_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=False,
                               download=True,
                               transform=transform)
test_loader = DataLoader(test_dataset,
                          shuffle=False,
                          batch_size=batch_size)

#定义模型
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
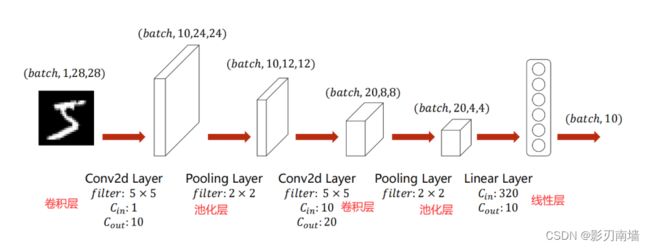
        self.conv1 = torch.nn.Conv2d(1,10,kernel_size=5)#定义卷积函数，输入通道数为1输出为10，卷积核大小为5
        self.conv2 = torch.nn.Conv2d(10,20,kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)#定义池化函数为最大池化
        self.fc = torch.nn.Linear(320,10)#线性层将320个特征减少为10个，分别对应最终输出结果
    #前馈
    def forward(self,x):
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))#先激活再池化
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size,-1)
        x = self.fc(x)
        return x

model = Net()

accuracy_list = []
epoch_list = []

#构造损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

#训练函数
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        #前馈
        inputs, target = data
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()#后馈
        optimizer.step()#更新

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            #这里为什么除以2000，没太明白
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx +1 ,running_loss /2000))
            running_loss = 0.0

#测试函数
def test(epoch):
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            inputs, target = data
            outputs = model(inputs)
            _,predicted = torch.max(outputs.data, dim=1)
            total += target.size(0)
            correct += (predicted == target).sum().item()
    print('Accuracy on test set: %d %% [%d/%d]' % (100 * correct / total, correct, total))
    accuracy_list.append(correct / total)
    epoch_list.append(epoch)

#主函数
if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test(epoch)
    plt.plot(epoch_list, accuracy_list)
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.show()

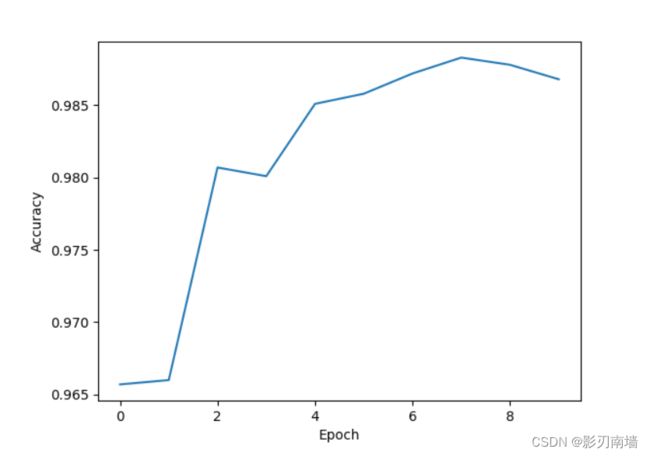
训练效果，识别准确率达到了98%，但是出现了过拟合的问题使得准确率下降

[10, 300] loss: 0.005
[10, 600] loss: 0.005
[10, 900] loss: 0.005
Accuracy on test set: 98 % [9880/10000]

第十一讲 卷积神经网络高级 5/5

**1X1的卷积有什么好处？**减小计算次数

复杂卷积神经网络：分支，循环结构

简单卷积神经网络：线性，全连接网络

复杂模块：用类封装，重用减少代码冗余

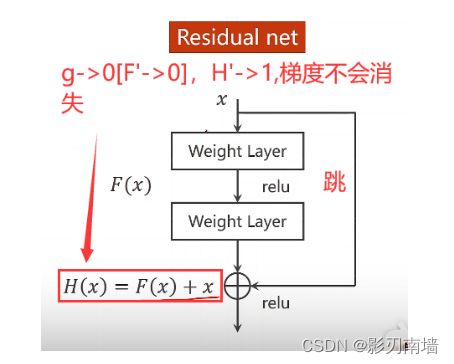
梯度消失及解决，梯度爆炸

解决方案是+X，如下

训练轮次是不是越多越好？

训练轮次并不是越多越好，过多可能训练效果反而下降，这就是过拟合了，解决方案是每当训练效果达到一个峰值，把参数保存下来，这样到最后训练出来的参数是最优的。

Python代码实现复杂卷积神经网络

训练效果

第十二讲 循环神经网络RNN基础 5/8

引言 显然，面对序列问题，即处理视频流、预测天气、自然语言等等问题时，此时输入的x1⋯xn实际上是一组有序列性即存在前后关系的样本。每个xi为一个样本的所包含的特征元组。

针对这样的问题，我们也会想到利用线性的全连接网络来进行处理，但事实上，全连接网络所需要计算的权重太多，并不能够解决问题。

**hidden隐藏层？**中间输出结果，作为下一轮的输入参与运算，体现了序列的依赖关系。

激活函数tanh∈[-1，1]

在RNN计算过程中，分别对输入xtx_txt以及前文的隐藏层输出ht−1h_{t-1}ht−1进行线性计算，再进行求和，对所得到的一维向量，利用tanh激活函数进行激活，由此可以得到当前隐藏层的输出hth_tht,其计算过程如下：

$$h_t=tanh(W_{ih}{x}_t+b_{ih}+W_{hh}{h}_{t-1}+b_{hh})$$

实际上，在框中的RNN Cell，的计算过程中为线性计算。
$$W_{hh}{h}_{t-1}+W_{ih}{x}_t=\left[\begin{array}{cc}{W}_{hh}& W_{ih}\end{array}\right]\left[\begin{array}{c}h\\ x\end{array}\right]$$

即在实际运算的过程中，这两部分是拼接到一起形成矩阵再计算求和的，最终形成一个大小为hidden_size×1hidden_size \times 1hidden_size×1的张量。

权重共享？ ** 给定一张输入图片，用一个固定大小的卷积核去对图片进行处理，卷积核内的参数即为权重**，而卷积核是对输入图片进行步长为stride的扫描计算，也就是说原图中的每一个像素都会参与到卷积计算中，因此，对于整个卷积核而言，权重都是一样的，即共享

多层RNN网络图

RNN应用场景：上下文语义识别[前后序列]、天气预测[时间序列] h1=f(x1,h0),后层输出结果依赖于前层的输出

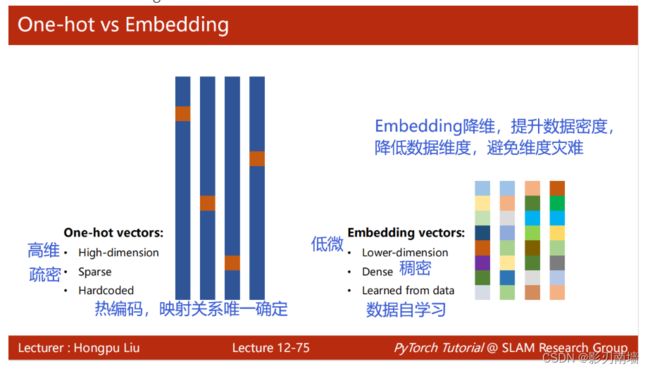
独热编码用来将字符转换成编码向量，避免123这种大小关系

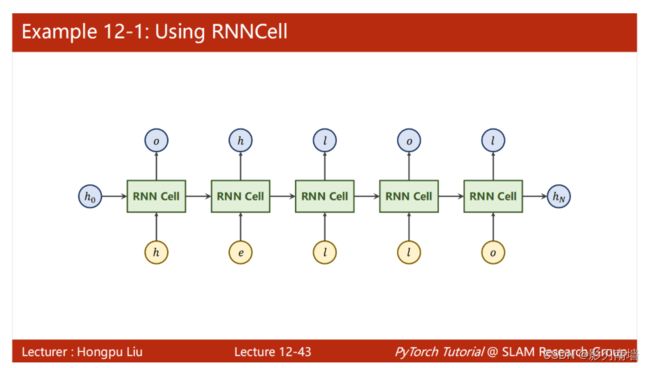
一个RNN实例，训练hello->ohlol

RNN计算图

One-Hot VS Embedding

LSTM和GRU是什么

python代码实现

CNNCell.py

#coding=utf-8
import torch

batch_size = 1
seq_len = 3
input_size = 4
hidden_size =2

cell = torch.nn.RNNCell(input_size = input_size, hidden_size = hidden_size)
#维度最重要
dataset = torch.randn(seq_len,batch_size,input_size)
print(dataset)

#初始化时设为零向量
hidden = torch.zeros(batch_size, hidden_size)

for idx,input in enumerate(dataset):
    print(idx,input)
    print('=' * 20,idx,'=' * 20)
    print('Input size:', input.shape)

    hidden = cell(input, hidden)

    print('outputs size: ', hidden.shape)
    print(hidden)
    

CNN.py

#coding=utf-8
import torch

batch_size = 1#批大小
seq_len = 5#序列长度
input_size = 4#输入特征维数
hidden_size =2#隐藏层数量
num_layers = 3#RNN层数
#其他参数
#batch_first=True 维度从(SeqLen*Batch*input_size)变为（Batch*SeqLen*input_size）
cell = torch.nn.RNN(input_size = input_size, hidden_size = hidden_size, num_layers = num_layers)

inputs = torch.randn(seq_len, batch_size, input_size)
print(inputs)
#初始化为0
hidden = torch.zeros(num_layers, batch_size, hidden_size)
print(hidden)
out, hidden = cell(inputs, hidden)
print(out)
print("Output size: ", out.shape)
print("Output: ", out)
print("Hidden size: ", hidden.shape)
print("Hidden: ", hidden)

第十三讲 循环神经网络进阶

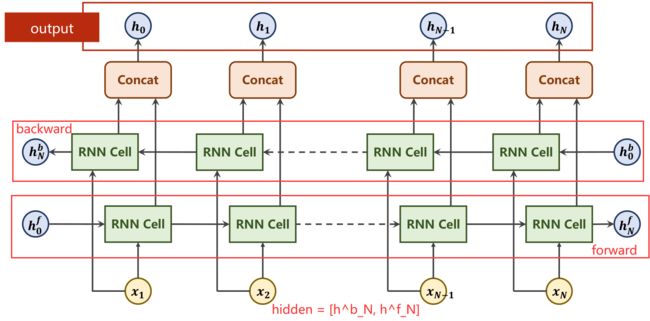
在RNN/LSTM/GRU中，都存在双向神经网络这一结构。

在双向计算过程中，对于序列x1…xn而言，分别进行x1→xn的前向计算和xn→x1的反向计算。

则对于同一个xi而言，有前向计算结果hif，以及反向计算结果hib，将两者进行连接（Concat）即可得到xi经过序列的最终结果hi.

对于RNN系列的网络而言，其输出包括output以及hidden两部分。其中的output指的是序列对应输出h1…hn形成的输出序列。hidden指的是隐含层最终输出结果，在双向网络中即为[hNf,hNb]

小案例 假定现在有一份关于名字的数据集，其部分数据如图所示。

核心问题在于，判断数据集中的每个名字所属的国家，共有18个国家类别。显然，每个国家或地区的人取名字都有其自己独特的语言习惯，因此可以利用RNN分析其名字（字符串）的潜在特点来进行分类。

python代码实现

#coding=utf-8
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.utils.data import DataLoader
from torch.utils.data import Dataset
import gzip
import csv
import time
from torch.nn.utils.rnn import pack_padded_sequence
import math
#可不加
import os
os.environ["KMP_DUPLICATE_LIB_OK"]  =  "TRUE"

BATCH_SIZE = 1

#count time
def time_since(since):
    s = time.time() - since
    m = math.floor(s / 60)
    s -= m*60
    return '%dm %ds' % (m, s)

# prepare dataset
class NameDataset(Dataset):
    def __init__(self, is_train_set=True):

        #读数据
        filename = 'names_train.csv.gz' if is_train_set else 'names_test.csv.gz'
        with gzip.open(filename, 'rt') as f:
            reader = csv.reader(f)
            rows = list(reader)

        #数据元组（name,country）,将其中的name和country提取出来，并记录数量
        self.names = [row[0] for row in rows]
        self. len = len(self.names)
        self.countries = [row[1] for row in rows]

        #将country转换成索引
        #列表->集合->排序->列表->字典
        self.country_list = list(sorted(set(self.countries)))
        self.country_dict = self.getCountryDict()
        #获取长度
        self.country_num = len(self.country_list)

    #获取键值对，country(key)-index(value)
    def __getitem__(self, index):
        return self.names[index], self.country_dict[self.countries[index]]

    def __len__(self):
        return self.len

    def getCountryDict(self):
        country_dict = dict()
        for idx,country_name in enumerate(self.country_list, 0):
            country_dict[country_name]=idx
        return country_dict

    #根据索引返回国家名
    def idx2country(self, index):
        return self.country_list[index]

    #返回国家数目
    def getCountriesNum(self):
        return self.country_num

#prepare and load dataset
trainset = NameDataset(is_train_set = True)
trainloader = DataLoader(trainset, batch_size=BATCH_SIZE, shuffle=True)

testset = NameDataset(is_train_set=False)
testloader = DataLoader(testset, batch_size=BATCH_SIZE, shuffle=False)

#最终的输出维度
N_COUNTRY = trainset.getCountriesNum()

#using model
class RNNClassifier(torch.nn.Module):
    def __init__(self, input_size, hidden_size, output_size, n_layers =1 , bidirectional = True):
        super(RNNClassifier, self).__init__()
        self.hidden_size = hidden_size
        self.n_layers = n_layers
        self.n_directions = 2 if bidirectional else 1
        #Embedding层输入 （SeqLen，BatchSize）
        #Embedding层输出 （SeqLen，BatchSize，HiddenSize）
        #将原先样本总数为SeqLen，批量数为BatchSize的数据，转换为HiddenSize维的向量
        self.embedding = torch.nn.Embedding(input_size, hidden_size)
        #bidirection用于表示神经网络是单向还是双向
        self.gru = torch.nn.GRU(hidden_size, hidden_size, n_layers, bidirectional = bidirectional)
        #线性层需要*direction
        self.fc = torch.nn.Linear(hidden_size * self.n_directions, output_size)

    def _init_hidden(self, batch_size):
        hidden = torch.zeros(self.n_layers * self.n_directions, batch_size, self.hidden_size)

        return create_tensor(hidden)

    #forward
    def forward(self, input, seq_length):
        #对input进行转置
        input = input.t()
        batch_size = input.size(1)

        #（n_Layer * nDirections, BatchSize, HiddenSize）
        hidden = self._init_hidden(batch_size)
        #(SeqLen, BatchSize, HiddenSize)
        embedding = self.embedding(input)

        #对数据计算过程提速
        #需要得到嵌入层的结果（输入数据）及每条输入数据的长度
        gru_input = pack_padded_sequence(embedding, seq_length)

        output, hidden = self.gru(gru_input, hidden)

        #如果是双向神经网络会有h_N^f以及h_1^b两个hidden
        if self.n_directions == 2:
            hidden_cat = torch.cat([hidden[-1], hidden[-2]], dim=1)
        else:
            hidden_cat = hidden[-1]

        fc_output = self.fc(hidden_cat)

        return fc_output

#ord()取ASCII码值
def name2list(name):
    arr = [ord(c) for c in name]
    return arr, len(arr)

#change tensor
def create_tensor(tensor):
    if USE_GPU:
        device = torch.device("cuda:0")
        tensor = tensor.to(device)
    return tensor

def make_tensors(names, countries):
    sequences_and_length = [name2list(name) for name in names]
    #取出所有的列表中每个姓名的ASCII码序列
    name_sequences = [s1[0] for s1 in sequences_and_length]
    #将列表车行度转换为LongTensor
    seq_lengths = torch.LongTensor([s1[1] for s1 in sequences_and_length])
    #将整型变为长整型
    countries = countries.long()

    #做padding
    #新建一个全0张量大小为最大长度-当前长度
    seq_tensor = torch.zeros(len(name_sequences), seq_lengths.max()).long()
    #取出每个序列及其长度idx固定0
    for idx, (seq, seq_len) in enumerate(zip(name_sequences, seq_lengths), 0):
        #将序列转化为LongTensor填充至第idx维的0到当前长度的位置
        seq_tensor[idx, :seq_len] = torch.LongTensor(seq)

    #返回排序后的序列及索引
    seq_length, perm_idx = seq_lengths.sort(dim = 0, descending = True)
    seq_tensor = seq_tensor[perm_idx]
    countries = countries[perm_idx]

    return create_tensor(seq_tensor),create_tensor(seq_length),create_tensor(countries)

#train
def trainModel():
    total_loss = 0
    for i, (names, countries) in enumerate(trainloader, 1):
        inputs, seq_lengths, target = make_tensors(names, countries)
        output = classifier(inputs, seq_lengths)
        loss = criterion(output, target)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        total_loss += loss.item()

        if i % 10 == 0:
            print(f'[{time_since(start)}] Epoch {epoch} ', end='')
            print(f'[{i * len(inputs)}/{len(trainset)}]', end='')
            print(f'loss={total_loss / (i * len(inputs))}')

    return total_loss

#test
def testModel():
    correct = 0
    total = len(testset)
    print("evaluating trained model……")
    with torch.no_grad():
        for i, (names, countries) in enumerate(testloader, 1):
            inputs, seq_lengths, target = make_tensors(names, countries)
            output = classifier(inputs, seq_lengths)
            pred = output.max(dim=1, keepdim=True)[1]
            correct += pred.eq(target.view_as(pred)).sum().item()

        percent = '%.2f' % (100*correct/total)
        print(f'Test set: Accuracy {correct}/{total} {percent}%')
    return correct/total


if __name__ == '__main__':
    '''
    N_CHARS：字符数量，英文字母转变为One-Hot向量
    HIDDEN_SIZE：GRU输出的隐层的维度
    N_COUNTRY：分类的类别总数
    N_LAYER：GRU层数
    '''
    USE_GPU = False
    N_CHARS = 10
    HIDDEN_SIZE = 2
    N_LAYER = 2
    N_EPOCHS = 10

    classifier = RNNClassifier(N_CHARS, HIDDEN_SIZE, N_COUNTRY, N_LAYER)
    #迁移至GPU
    if USE_GPU:
        device = torch.device("cuda:0")
        classifier.to(device)

    criterion = torch.nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(classifier.parameters(), lr=0.001)

    start = time.time()
    print("Training for %d epochs ... " % N_EPOCHS)
    #记录训练准确率
    acc_list = []
    for epoch in range(1, N_EPOCHS+1):
        #训练模型
        trainModel()
        #检测模型
        acc = testModel()
        acc_list.append(acc)

    #绘制图像
    epoch = np.arange(1, len(acc_list)+1, 1)
    acc_list = np.array(acc_list)
    plt.plot(epoch, acc_list)
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.grid()
    plt.show()

比较

穷举法【遍历某个区间】------[有方向，利用梯度，会比较快]-------->梯度下降【用整个数据集更新一次权重】------[克服鞍点，性能上升，时间复杂度变高]-------->随机梯度【用单个样本点更新一次权重】