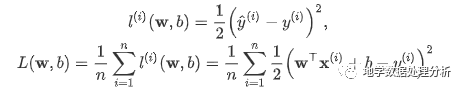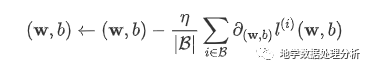线性回归模型_深度学习线性回归模型

---

今天来介绍深度学习中的线性回归，并以空气质量数据为例，得出AQI指数和PM2.5、PM10、SO2等监测量之间的关系。最后采用Pytorch实现该例子。 数据来源可参考文章：[空气质量指数]

线性回归模型主要包括模型部分(即线性关系)、数据集、损失函数、优化函数这几个基本要素。

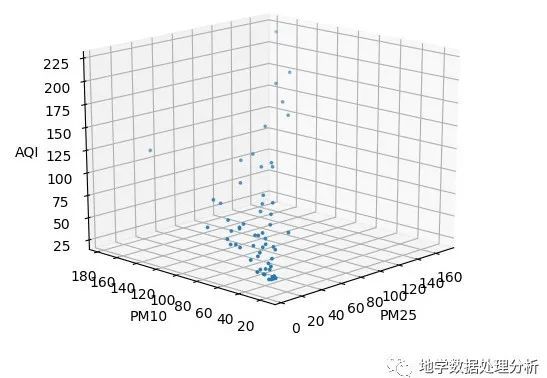
0 1模型根据我们所拥有的数据，假设AQI指数只取决于PM25, PM10, SO2, CO, NO2, O3这几个因素。线性回归假设输出与各个输入之间是线性关系，即:

02数据集通常会收集一系列的真实数据，并在这个数据上面寻找模型参数来使模型的预测AQI值与真实AQI值的误差最小。这个数据集被称为训练数据集(training data set)或训练集(training set)，一条监测记录被称为一个样本(sample)，其AQI值叫作标签(label)，用来预测标签的因素叫作特征(feature)。特征用来表征样本的特点。选取PM2.5和PM10这两个特征进行展示，其与AQI的三维图如下：

03损失函数在模型训练中，我们需要衡量价格预测值与真实值之间的误差。通常会选取一个非负数作为误差，且数值越小表示误差越小。一个常用的选择是平方函数。它在评估索引为i的样本误差的表达式为：

04优化函数 - 随机梯度下降当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解(analytical solution)。此处使用的线性回归和平方误差属于这个范畴。然而，大多数深度学习模型并没有解析解，即模型特别复杂，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。在求数值解的优化算法中，小批量随机梯度下降(mini-batch stochastic gradient descent)在深度学习中被广泛使用。它的算法很简单：先选取一组模型参数的初始值，一般是随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)，然后求小批量中数据样本的平均损失有关模型参数的导数(梯度)，最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

学习率: η代表在每次优化中，能够学习的步长的大小

批量大小: B是小批量计算中的批量大小(batch size)

总结一下，优化函数的有以下两个步骤：

(i)初始化模型参数，一般来说使用随机初始化；

(ii)在数据上迭代多次，通过在负梯度方向移动参数来更新每个参数。

05实现

import torchimport torch.utils.data as Datafrom torch import nnfrom torch.nn import initimport torch.optim as optimfrom matplotlib import pyplot as pltfrom mpl_toolkits.mplot3d import Axes3Dimport numpy as npimport pandas as pd# 初始化参数，一般是随机生成def init_parameters(num_inputs):  w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)  b = torch.zeros(1, dtype=torch.float32)  w.requires_grad_(requires_grad=True)  b.requires_grad_(requires_grad=True)  return w, b# 模型: 线性模型def model(X, w, b):  return torch.mm(X, w) + b# 损失函数def squared_loss(y_hat, y):   return (y_hat - y.view(y_hat.size())) ** 2 / 2# 优化函数-梯度下降def sgd(params, lr, batch_size):   for param in params:    param.data -= lr * param.grad / batch_size

06 训练

此处每个小批量有3个样本，并重复训练100次来迭代模型参数。

def main():  # super parameters init  lr = 0.00005 # 学习的步长的大小  num_epochs = 100 # 训练重复次数  batch_size = 3 # 批量大小  features, labels = loadData("data.txt")  # set input feature number   num_inputs = features.shape[1]  # set example number  num_examples = features.shape[0]  w, b = init_parameters(num_inputs)  net = model  loss = squared_loss  # training  for epoch in range(num_epochs):  # # 训练重复次数    for X, y in read_data_batch(batch_size, features, labels):      l = loss(net(X, w, b), y).sum()      l.backward() # 后向传播计算梯度       sgd([w, b], lr, batch_size)  # 小批量随机梯度下降更新模型参数      w.grad.data.zero_() # 梯度清零      b.grad.data.zero_()    train_l = loss(net(features, w, b), labels)    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

0 7结果

# 当 lr = 0.00005, num_epochs = 100, batch_size = 5时...epoch 98, loss 32.237270epoch 99, loss 23.895002epoch 100, loss 23.717735W: [[0.7877328991889954], [0.3964788615703583], [-0.12595394253730774], [0.05453995242714882], [0.01380900852382183], [0.19781270623207092]]b: [0.04311537370085716]# 当 lr = 0.0002, num_epochs = 100, batch_size = 5时epoch 1, loss 740278.187500epoch 2, loss 173101648.000000epoch 3, loss 114911019008.000000epoch 4, loss 6522003259392.000000epoch 5, loss 608186748006039552.000000epoch 6, loss 38219160520935604224.000000epoch 7, loss 2773605162385879859200.000000epoch 8, loss 1774152400068472209408.000000

可以看出，当学习率较小时，此迭代收敛(即损失函数值在变小)，也就得到了我们的线性回归模型参数W和b；但是增大学习率时，例如学习率为0.0002时，发现迭代在发散(损失函数值一直在增大)。因此，当发现损失函数值无法收敛时，可以尝试一下更小的学习率。 如需源码，请后台回复:  "线性回归"， 如有问题，可加微信 " wxid-3ccc ".

说说线性规划

泰勒图的MATLAB实现

Python爬取高德地图--瓦片图

高斯混合模型判定交通拥堵状态

ArcPy批量定义投影和批量投影转换

机器人局部规划算法--DWA算法原理

数据分享GIMMS NDVI 3gv1(1982-2015)

ArcGIS时间滑块实现车辆轨迹动态展示

GPS数据处理---在野外采样寻点中的应用

▼ 更多精彩推荐，敬请关注我们 ▼