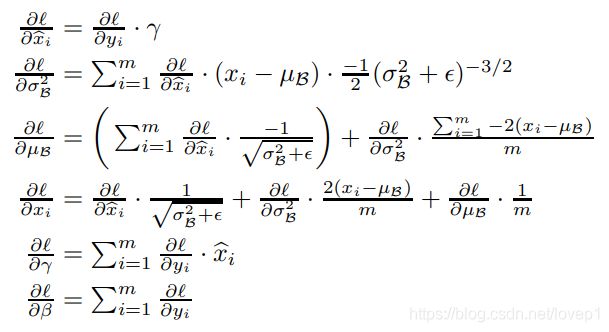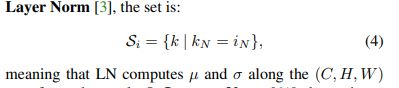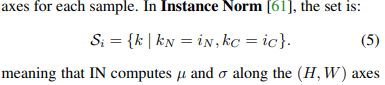详解常用的Batch Norm、Group Norm,Layer norm、Instance Norm
本文主要分析cv中常用的batch norm, group norm方法,由于目标检测中不常见,因此只是简单介绍并理解Layer norm和Instance Norm的概念。首先cv中用的最多的肯定是batch norm,后续凯明何大佬又提出了gropu norm,但是其实在检测领域里面还没有真正的普及,尤其是在工业界部署上面,用的最多的还是batch norm,尤其是前两年大量paper提出基于BN层的模型剪枝方法、基于BN的融合卷积计算方法等(本文不提及,后续文章有需要会单独分析此类论文)后,batch-norm凸显的更加重要了,本文将不按照论文结构解析。
1、batch norm
paper:https://arxiv.org/abs/1502.03167
首先我们直接看paper的摘要:在dnn的训练过程中,各层的参数发生变化,则每层的输入分布也会发生变化,此时则需要通过降低学习率和通过更为仔细的参数初始化来减慢训练速度,使得神经网络变成饱和的非线性的模型,这个现象称之为internal covariate shift(内部协变量偏移)。 更进一步的,通过将归一化变为模型的一部分,为每个训练的小批量数据执行归一化,这样可以在训练时使用更高的学习率,并且参数初始化时不用那么小心和仔细,同时充当正则化器,在某些情况下可以不适用droupout。(注意:这是原文提出的batch-norm的初衷,其他的网上流传的似是而非的功能都是扯淡的!!!!)
internal covariate shift:在训练过程中每层输入的分布会改变,因为前面层的参数在不断更新,意味着层会需要连续不断的去适应新的分布。我们称它经历了covariate shift
接下来我们直接看paper的重点,注意,从paper的结构来说,是从随机梯度下降开始描述的,但本文只讲其batch-norm的部分,如下:
如上图所示,在训练时,对其每个batch输入求均值和方差,然后将输入进行归一化,,此时再加上β偏移量,得到最终的输出值,则此时的输出值会呈现稳定的分布输出。此处的重点来了:为什么非要对normalize后的输入进行scale和shift,把输入拉到均值为0,方差为1的正态分布已经很棒了,这是因为使用了norm后95%的数值会落在[-2, 2]之间,对应的sigmod是类似线性区间,而我们的多层神经网络要求的是非线性激活,因此,会导致dnn没有意义,降低网络的表达能力,因此normalization后在经过scale+shift(注意:这个γ和β是可训练的,后续经典的剪枝算法之一就是利用γ来进行剪枝,再后续又提出了基于γ和β一起的剪枝方法)
此时bn层的链式求导法则如下:
其中L为损失函数,xi为输入特征,y为bn层输出特征、方差、β、γ参数就不提了,具体的公式推导此处不研究,有兴趣的同学可以仔细推理一下。接下来paper给出了整个bn层的算法流程:
如上图所示,简单介绍一下训练流程,看上去很复杂,去掉专业符号就很简单了,N代表所有的可训练参数,首先对每一层输入进行x(当前层网络计算值)->y(BN)的替换,在训练时优化N,同时优化γ和β,在测试时,frozen BN参数,取多个batch的均值作为推理时的参数,然后进行bn层的推理计算。
进一步的,paper提出,bn层的位置问题,bn层是放在非线性激活的前面还是后面的问题,回到原paper:
假定原始的卷积层结构如上,加入BN层后,变形为如下:
即明显可以看出,原paper中BN层的结构是放在激活函数前面的,但是实际上,到底BN层放在前面还是后面呢,有很多争论,目前来看,主流应该是放在激活函数前面,从而在进入激活函数前面时将深层网络的输出从饱和拉至不饱和,当然也有说放在后面的,能够提升是收敛速度并且解决过拟合问题,而且跟激活函数有关,具体怎么样,本文就不讨论了。
实验结果:
综上,BN层的paper重点就到这里技术了,总结一下,BN层的优点是什么呢?大大的加快了DNN的训练速度,并给网络的权重提供了正则化,一定程度上防止了过拟合的问题。
2、group norm
group-norm :https://arxiv.org/abs/1803.08494
Layer norm:https://arxiv.org/pdf/1607.06450.pdf
Instance norm:https://arxiv.org/pdf/1607.08022.pdf
本节详细介绍group norm,layer norm主要应用于RNN领域,在cnn领域效果不如BN,Instance norm主要用于风格迁移等,因此,本节只借用group norm对这两种方法进行概念解析,详情请参见原始paper。
2.1 batch-norm的缺点
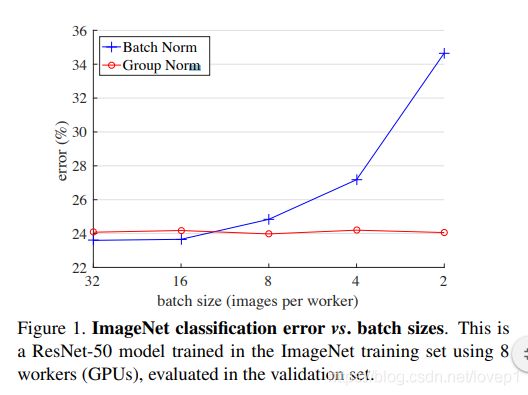
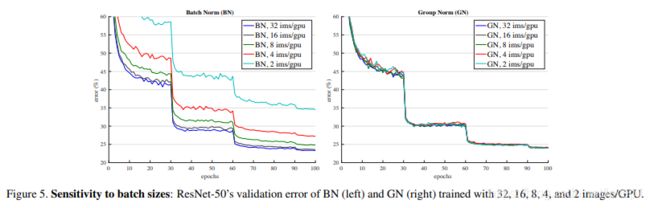
首先看到Batch-norm的缺点:极度依赖与batch_size的大小的问题,当bs较小时,当前的批数据的均值和方差没有办法代表整体输入数据的分布,此时效果就会变差,如下图所示:
从上图中,我们可以明显看出,当bs变小是,BN层的精度差异很大,而本paper提出来的layer-norm便不存在这个问题,那既然bs对精度影响这么大,能不能提出一个norm方法,剔除掉bs的影响,从而取代Batch norm呢,?paper提出了这个思想。
2.2 Norm方式的定义
首先来看定义,什么叫做BN,Layer Norm、Instance Norm、Group Norm。
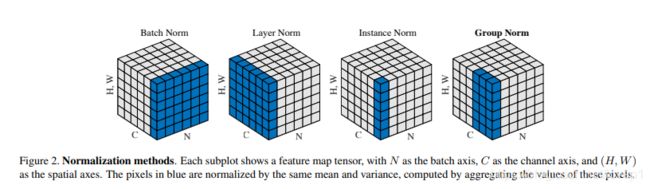
直接回到paper中给出的定义,如下图所示:
我们需要简单的说明一下这张图,很多博客都只是简单的举例,其实这张图还是有点抽象的。上图中,N代表batch-size的维度,H\W代表feature-map尺寸,C代表feature-map的通道数。但是上图是只有3个维度的,结合paper,是将H/W融合到了一个维度上,怎么理解呢,原来HW是一个面(二维),现在将其变成竖直的一条直线(1列-1维),其他维度不变,也就将4维变成了3维。
接下来我们看不同的norm方式:
BN是将整个N(batch-szie)维度归一化,对N维度的feature值求均值和方差,然后将特征点的值归一化;
Layer norm是将C维度进行归一化,对于每个输入数据的所有通道(整层),即所有feature-map,求其所有像素点的均值和方差;
Instance norm是对每个输入数据的单通道,即每张feature-map的单通道的像素点求均值和方差;
Group norm是将channels分为很多组,对每组求均值和方差,然后对每组进行归一化,则当group=1时,Group norm=Instance norm,当group=C时,Group norm=Instancenorm。
注意:BN需要通过滑动平均来记录全局的均值和方差,但是其他norm方法与batch无关,实现了训练与测试的统一。
2.3 Group norm的实现方式
idea来源,我们直接看paper:
从上图指出,视觉的表征的channels并不是独立的,sift、hog和gist等都是按照组设计的分组表示。类似的,cnn的特征也可以使用这种方式。
首先,paper给出了norm方法的一般形态,如式1:
其中均值和方差的定义如下式:
其中Si是代计算的均值和方差的像素集合,基于上式和Si的定义,我们分开讨论各种情况:
在batch-norm中,Si定义如下,其中ic和kc是在channel维度,如何理解呢,就是将channel-0的所有输入(N)维度做均值方差计算,将channel-1的所有输入(N)维度做均值方差计算,依次...,则最终体现的就是输入batch的归一化:
pytorch的api接口为: torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
在Layer norm中,Si被定义为式4,kn和in是在整个(c,h,w)维度,也就是以单张输入数据为单位计算均值和方差:
pytorch的api接口为:torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)
在Instance norm中,Si被定义为式5,kn和in是在整个HW维度上完成求和计算,也就是单通道、单输入的均值和方差计算:
pytorch的api接口为:torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
归一化后,最终通过下式来完成尺度和平移变换:
Group norm的定义如下(本文重点):
如上图所示,Group norm时将通道分组,每次计算取同一个输入(N)、一组通道(group channels)、所有hw的均值和方差,将以上维度的特征点数值进行归一化。
测试结果:
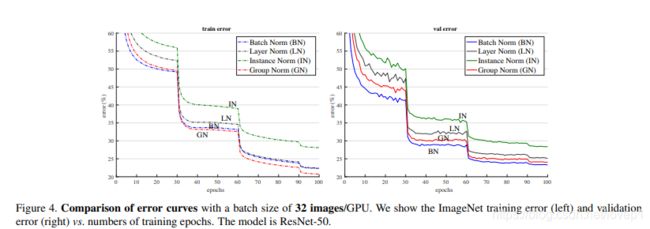
上述图像为res50的测试结果,我们可以看到,gn的norm方式在各个阶段都是最接近于bn和超过bn的方法。
最重要的,上图可以看出Group norm对batch-size不敏感,且当bn的batch-size变小时,效果是比Group-norm要差的。
综上,便是cv领域中常用的batch-norm和group-norm。