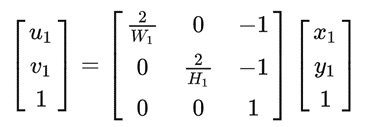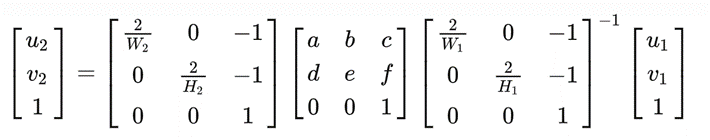Spatial Transformer Networks

【零基础科研】【论文推介】是作者结合实验室师弟师妹们打基础阶段，做的一些学习笔记，对相关方向的论文进行的一些记录，希望能够帮助到后续入坑的朋友。专栏不定期更新目前主要分享图像配准和图像融合两个方向的经典论文和前沿论文。

Spatial Transformer Networks

Paper:https://proceedings.neurips.cc/paper/2015/file/33ceb07bf4eeb3da587e268d663aba1a-Paper.pdf

---

---

对于计算机视觉任务来说,我们希望模型可以对于物体姿势或位置的变化具有一定的不变性,从而在不同场景下实现对于物体的分析。传统CNN中使用卷积和Pooling操作在一定程度上实现了平移不变性,但这种人工设定的变换规则使得网络过分的依赖先验知识,既不能真正实现平移不变性(不变性对于平移的要求很高),又使得CNN对于旋转,扭曲等未人为设定的几何变换缺乏应有的特征不变性。为此作者提出了Spatial Transformer Networks。

Spatial Transformer Networks(STN)作为一种新的学习模块,具有以下特点:
(1) 为每一个输入提供一种对应的空间变换方式(如仿射变换)
(2) 变换作用于整个特征输入
(3) 变换的方式包括缩放、剪切、旋转、空间扭曲等等
(4) 具有可导性质的STN不需要多余的标注,能够自适应的学到对于不同数据的空间变换方式。
它不仅可以对输入进行空间变换,同样可以作为网络模块插入到现有网络的任意层中实现对不同Feature map的空间变换，如下图所示：

1.STN的网络模型

每一个ST模块由Localisation net, Grid generator和Sample组成：
(1) Localisation net（参数预测）决定输入所需变换的参数θ：定位网络获取输入特征图，并通过多个隐藏层输出应该应用于特征图的空间变换参数——这给出了基于输入的变换条件。
(2) Grid generator（坐标映射）通过θ和定义的变换方式寻找输出与输入特征的映射T(θ)： 使用预测的变换参数来创建采样网格，该网格是一组点，输入映射应在其中采样以生成变换后的输出。
(3) Sampler（像素采集）结合位置映射和变换参数对输入特征进行选择并结合双线性插值进行输出：将特征图和采样网格作为采样器的输入，生成从网格点处的输入采样的输出图。

事实上，在这个过程中，我们需要面对三个主要的问题：
（1）这些参数应该怎么确定？
（2）图片的像素点可以当成坐标，在平移过程中怎么实现原图片与平移后图片的坐标映射关系？
（3）参数调整过程中，权值一定不可能都是整数，那输出的坐标有可能是小数，但实际坐标都是整数的，如果实现小数与整数之间的连接？

下面对于每一个组成部分进行具体介绍。

1.1 Localisation net

Localisation net输入为一张Feature map: $U\in R^{H_x{W}_{x}C}$ 。经过若干卷积或全连接操作后接一个回归层回归输出变换参数$\theta$ 。 的维度取决于网络选择的具体变换类型,如选择仿射变换则$\theta \in R^{2\times 3}$ 。如选择投影变换则$\theta \in R^{3\times 3}$ 。

1.2 Grid generator

Grid generator利用localisation层输出的 $\theta$, 对于Feature map进行相应的空间变换。设输入Feature map U每个像素位置的坐标为 $\left(x_i^s,y_i^s\right)$,经过ST后输出Feature map每个像素位置的坐标为 $\left(x_i^t,y_i^t\right)$ , 那么输入和输出Feature map的映射关系便为(选择变换方式为仿射变换)：

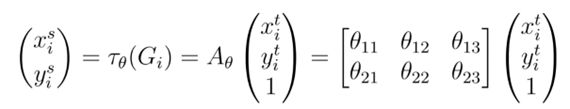
通常，输出像素位于规则网格$\mathbf{G}=\left\{G_i\right\}$上，各像素位置为$G_i=\left(x_i^t,y_i^t\right)$，形成输出特征图$V\in R^{H^{\prime }\times W^{\prime }\times C}$.

变换$T_{\theta }$也可以更一般，如具有8个参数的平面射影变换、分段仿射或薄板样条。事实上，变换可以有任何参数化形式，只要它对参数可微——这至关重要的允许梯度从样本点$T_{\theta }(G)$反向传播到定位网络输出$\theta$ 。

【个人理解】
空间变换是对像素点所处位置的变换，可以是输入到输出的映射，也可以是输出到输入的映射。一定要注意，这是像素位置（或坐标）的映射，而不是像素值的映射。即G是输出图V的位置坐标， $T_{\theta }(G)$是输入图U的位置坐标（根据G和θ算出）。

我们是根据输出计算输入，即根据G和$\theta$计算 $T_{\theta }(G)$ 。

为什么是输出坐标到输入坐标的映射，一个比较满意的解释是坐标映射的作用，其实是让目标图片在原图片上采样，每次从原图片的不同坐标上采集像素到目标图片上，而且要把目标图片贴满，每次目标图片的坐标都要遍历一遍，是固定的，而采集的原图片的坐标是不固定的，因此用这样的映射。

对于输入和输出坐标，我们会使用了宽度和高度标准化的坐标系，即将坐标规范在-1~1（pytorch中是这样处理的）。

1.3 Sampler

在上一步，对于输出Feature map的每一个位置,我们对其进行空间变换(仿射变换)寻找其对应与输入Feature map的空间位置,如果这一步的输出为整数值(往往不可能),也就是经过变换后的坐标可以刚好对应原图的某些空间位置,那么ST的任务便完成了,即输入图像在Localisation net和Grid generator后先后的确定了空间变换方式和映射关系。

由于计算出的输入位置$T_{\theta }(G)$一般不为整数，所以需要插值操作。

我们从可微的角度来讲，为什么必须插值？为什么把小数变为整数不行？

上图中，根据空间变换，我们发现输出特征图坐标（0.6，0.4）对于输入特征图坐标（1.6，2.4），那么我们的想法是将（1.6，2.4）取整，为（2，2），然后取（2，2）位置上的像素值填到输出特征图坐标（0.6，0.4）上。

梯度下降是一步一步调整的，而且调整的数值都比较小。比如一步迭代后，结果有：1.6→1.64,2.4→2.38，那么（1.64，2.38）依然取整变为（2，2），即坐标对应仍然不变。那么此时梯度为0，我们没有办法微分了，就没有办法根据SGD进行优化。所以我们需要插值：


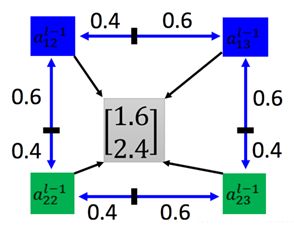
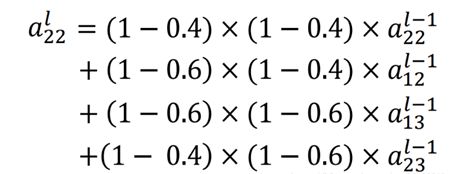
四个点对应的权值都是与结果对应的距离相关的，如果目标图片发生了小范围的变化，这个式子也是可以捕捉到这样的变化的，这样就能用梯度下降法来优化了。

论文作者对我们前面的过程给出了非常严密的证明过程：
每次变换，相当于从原图片中，经过仿射变换，确定目标图片的像素点坐标的过程,这个过程可以用公式表示为：

说明如下：

• k：kernel(采样核)，表示一种插值方法（比如双线性插值），k（）是可导的，两个k是分别在x和y方向上插值，
• Φx和Φy：定义图像插值的通用采样核k()的参数，
• $U_{nm}^c$：输入通道c中位置(n, m)处的值，
• $V_m^c$：通道c中位置$\left(x_i^t,y_i^t\right)$处像素i的输出值。
• 注意，输入的每个通道的采样都是相同的，因此每个通道都以相同的方式进行转换(这保持了通道之间的空间一致性)。
  
  这里i从0到$H^{\prime }\times W^{\prime }$,也就是把输出图展开，相当于把坐标矩阵变成坐标向量。
  如果使用双线性插值，可以有：
  

通过max函数选择与输出$\left(x_i^s,y_i^s\right)$距离小于1的像素位置,距离$\left(x_i^s,y_i^s\right)$越近的点被分配了越高的权重,实现了使用$\left(x_i^s,y_i^s\right)$周围四个点的score计算最终score,我们可以有如下偏导数计算公式:

对于$y_i^s$的求导与$x_i^s$类似,因而我们可以求得对于$\theta$的偏导:

其中， $\frac{\partial x_i^s}{\partial \theta },\frac{\partial y_i^s}{\partial \theta }$可根据具体的变换函数便可得到。

2.STN的代码实现

2.1 Pytorch官方源码

Pytorch官方给出了实现代码，网址如下：STN-pytorch代码实现
这里我们假设Mnist数据集作为网络输入:
(1)首先定义Localisation net的特征提取部分,为两个Conv层后接Maxpool和Relu操作:

# Spatial transformer localization-network
self.localization = nn.Sequential(
            nn.Conv2d(1, 8, kernel_size=7),
            nn.MaxPool2d(2, stride=2),
            nn.ReLU(True),
            nn.Conv2d(8, 10, kernel_size=5),
            nn.MaxPool2d(2, stride=2),
            nn.ReLU(True)
        )

(2)定义Localisation net的变换参数θ回归部分,为两层全连接层内接Relu:

# Regressor for the 3 * 2 affine matrix
        self.fc_loc = nn.Sequential(
            nn.Linear(10 * 3 * 3, 32),
            nn.ReLU(True),
            nn.Linear(32, 3 * 2)
        )

(3)在nn.module的继承类中定义完整的STN模块操作:

# Spatial transformer network forward function
    def stn(self, x):
        xs = self.localization(x)
        xs = xs.view(-1, 10 * 3 * 3)
        theta = self.fc_loc(xs)
        theta = theta.view(-1, 2, 3)

        grid = F.affine_grid(theta, x.size())
        x = F.grid_sample(x, grid)

        return x

    def forward(self, x):
        # transform the input
        x = self.stn(x)

        # Perform the usual forward pass
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

跑了20个epoch之后，结果如下：

2.2 自己实现

其实，自己实现STN也很简单。需要实现仿射变换和双线性插值这两块内容。笔者根据网上的资料，自己尝试写了出来。由于还没来得及整理，所以先拖一拖（hhh）

2.3 放射变换中的坐标系

我们在前面也提到过，在Pytorch的实现中，是把坐标系规范到-1~1之间的。
theta为N×2×3的变换矩阵。
grid定义在左上[-1,-1]，右下[1,1]的归一化坐标系下。
假设在高为H1，宽为W1的原图上有点(x1,y1)，经过仿射变换矩阵M作用后得到高为H2，宽为W2的目标图上的点(x2,y2)，则有：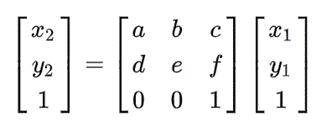
说明：我们刚说到theta为N×2×3的变换矩阵，但是这里可以看到它是N×3×3。但是它只有a,b,c,d,e,f六个参数，其实写成2×3也是可以的。
点(x1,y1)在pytorch归一化坐标系中的位置(u1,v1)为：

写成矩阵形式为：

同理，有：

因此在pytorch归一化坐标系，仿射变换公式为：

3.参考链接

1. https://zhuanlan.zhihu.com/p/349741938
2. https://zhuanlan.zhihu.com/p/41738716
3. https://arleyzhang.github.io/articles/7c7952f0/
4. https://blog.csdn.net/qq_39422642/article/details/78870629