数字图像处理第三章part2
chap03-空间滤波基础
本节对应原书第三章的后半部分,第三章主讲图像增强,借机引入空间滤波,空间域分析和频率域分析后都会涉及。
从时域信号引入频率和空间频率
前面说过信号可以理解为函数。由于时间只有一个维度,时域信号自然就是一个只有一个自变量的函数:比如一个声波

在 0 ∼ 2 π 0\sim2\pi 0∼2π上有两个波形,那么频率为 1 / π H z 1/\pi\ Hz 1/π Hz,振幅为2。
在 2 π ∼ 4 π 2\pi\sim4\pi 2π∼4π上有四个波形,频率为 2 / π H z 2/\pi\ Hz 2/π Hz,振幅为4。后面的这段信号相比前一段是高频的。
在声波中,声调和频率成正比,响度和振幅成正比。
联想一下,一幅数字图像,是一个二维空间域离散信号。其每个像素的值对应的是声波中的振幅,与能量相关,在这里不重要;重要的是,图像的频率怎么判断?
时域对应的是空间域,但是空间域是二维的,方向有很多,就像一元函数说求导,二元函数不说求导,说求梯度。不考虑方向的话,那将二维图像的一行或者一列取出,像素最高值和最低值对应振幅,像素值震荡的快慢对应频率,空间对应时间,那么分析的方法就是一样的。
图像的低频对应着图像灰度变化缓慢的区域,图像的高频对应着图像灰度变换剧烈的区域:
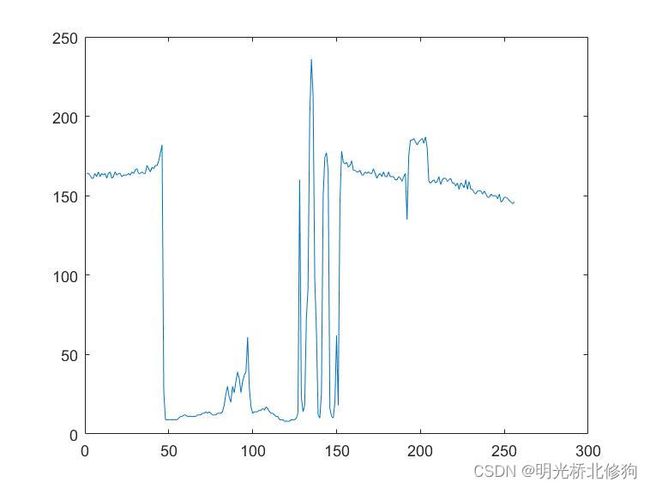
如上的图像,取中间那一行像素:
(如果变化很小的地方视为不变化)。可以看出 0 ∼ 50 0\sim50 0∼50对应低频, 50 50 50处是背景天空和摄影师的边缘, 100 100 100左边一点有一些高频对应摄影师的手套, 125 ∼ 150 125\sim150 125∼150有很多高频,对应拍摄架, 200 200 200处也有两个高频,对应大楼。
那么高频一般对应着边缘信息、细节。同时,由于成像设备和数字化计算机的缺陷,噪声无处不在,噪声也是高频。低频一般对应灰度变换缓慢的区域。如果仅保留图像的低频分量,那么可以从低频分量看出图像的整体变化趋势;如果仅保存高频分量(边缘,细节和噪声),则可以看出图像的细节信息。
对图像滤波就是滤出这些高频低频,中频的过程。低通滤波(Low-pass filtering),人如其名,低频通过,模糊整幅图像,对图像进行平滑处理。高通滤波(High-pass filtering),得到图像的边缘。空间滤波通过将像素的值替换成该像素及其邻域的函数值进行修改图像,如果执行的运算是线性的,则成为线性滤波,否则,称为非线性滤波。
空间相关和卷积
相关指的是一个信号与另一个延时信号的相关程度,在时域中,两个信号 f 1 ( t ) , f 2 ( t ) f_1(t),f_2(t) f1(t),f2(t)的相关定义为:
R 12 = ∫ − ∞ ∞ f 1 ( t ) f 2 ( t − τ ) d t R_{12}=\int_{-\infty}^{\infty}f_1(t)f_2(t-\tau)dt R12=∫−∞∞f1(t)f2(t−τ)dt
类比到离散空间域:
g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) g(x,y)=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x+s,y+t) g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
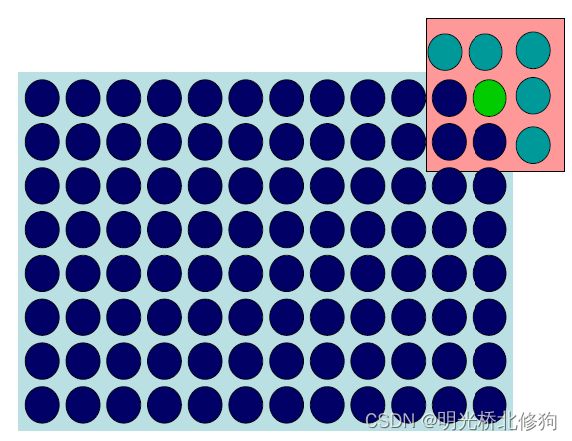
含义为滤波器核w的对影项和f的对应项相乘再求和,算子w在图像f上以步长为1进行滑动,填充方式默认为0填充(记得图像处理的输入和输出都是数字图像,因此这里没有别的条件,输入输出图像大小应一致)
其中,x,y是图像上的点坐标,算子的高等于 2 a + 1 2a+1 2a+1,宽等于 2 b + 1 2b+1 2b+1,如下图一个3x3的算子(a=1,b=1):

那么相关运算就相当于:
g ( x , y ) = w ( − 1 , − 1 ) f ( x − 1 , y − 1 ) + w ( − 1 , 0 ) f ( x − 1 , y ) + ⋯ + w ( 0 , 0 ) f ( x , y ) + ⋯ + w ( 1 , 1 ) f ( x + 1 , y + 1 ) g(x,y)=w(-1,-1)f(x-1,y-1)+w(-1,0)f(x-1,y)+\cdots+w(0,0)f(x,y)+\cdots+w(1,1)f(x+1,y+1) g(x,y)=w(−1,−1)f(x−1,y−1)+w(−1,0)f(x−1,y)+⋯+w(0,0)f(x,y)+⋯+w(1,1)f(x+1,y+1)
与卷积的区别
在时域中,离散卷积定义为:
g [ n ] = ∑ k = − ∞ ∞ w [ k ] f [ n − k ] g[n]=\sum_{k=-\infty}^{\infty}w[k]f[n-k] g[n]=k=−∞∑∞w[k]f[n−k]
相关应该是:
g [ n ] = ∑ k = − ∞ ∞ w [ n ] f [ n − k ] g[n]=\sum_{k=-\infty}^{\infty}w[n]f[n-k] g[n]=k=−∞∑∞w[n]f[n−k]
所以,卷积实际上就是先将其中一个信号翻转再与另一个信号进行相关运算。在空间域中也是如此。那么,如果滤波器核是中心对称的,用这个核卷积图像,还是相关图像,结果是相同的。
卷积运算的性质
-
完全卷积
如果卷积运算后还想维持原图大小,那么输入图像应该在四周进行填充,如果核的大小为 m × n m\times n m×n,那么顶部和底部分别要填充(m-1)个像素,左边右边分别要填充(n-1)个像素。
-
交换律
∫ − ∞ ∞ x ( τ ) h ( t − τ ) d τ , 将 t − τ 替换为 T ∫ ∞ − ∞ x ( t − T ) h ( T ) d ( − T ) = ∫ − ∞ ∞ x ( t − T ) h ( T ) d T \int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau,将t-\tau替换为T\\ \int_{\infty}^{-\infty}x(t-T)h(T)d(-T)=\int_{-\infty}^{\infty}x(t-T)h(T)dT ∫−∞∞x(τ)h(t−τ)dτ,将t−τ替换为T∫∞−∞x(t−T)h(T)d(−T)=∫−∞∞x(t−T)h(T)dT
可得 x ( t ) ∗ h ( t ) = h ( t ) ∗ x ( t ) x(t)*h(t)=h(t)*x(t) x(t)∗h(t)=h(t)∗x(t) -
因为满足交换率,就可以推出卷积也满足结合律
-
分配律是卷积和相关都满足的性质
有时候,图像是被顺序的、分阶段的滤波的,每个阶段使用的核不相同。如,对于施加在f上的Q个阶段的滤波,首先使用 w 1 w_1 w1,再使用 w 2 w_2 w2。。。利用结合率
w = w 1 ∗ w 2 ∗ w 3 ∗ ⋯ ∗ w Q w=w_1*w_2*w_3*\cdots*w_Q w=w1∗w2∗w3∗⋯∗wQ
可最后对图像f使用w滤波
g = f ∗ w g=f*w g=f∗w
减小计算量。其中w竖直方向长度和水平方向长度分别为
W v = Q × ( m − 1 ) + m W h = Q × ( n − 1 ) + n W_v=Q\times(m-1)+m\\ W_h=Q\times(n-1)+n Wv=Q×(m−1)+mWh=Q×(n−1)+n
填充以保持图像大小。
可分离滤波器核
若二维函数 G ( x , y ) G(x,y) G(x,y)可以写成以为函数 G 1 ( x ) , G 2 ( x ) G_1(x),G_2(x) G1(x),G2(x)的乘积 G ( x , y ) = G 1 ( x ) G 2 ( y ) G(x,y)=G_1(x)G_2(y) G(x,y)=G1(x)G2(y),那么称它是可分离的,空间滤波器核是一个矩阵,可分离核可表示为两个向量的外积如:
w = [ 1 1 1 1 1 1 ] = [ 1 1 ] [ 1 1 1 ] w=\begin{bmatrix} 1&1&1\\ 1&1&1 \end{bmatrix}=\begin{bmatrix}1\\1\end{bmatrix}\begin{bmatrix}1&1&1\end{bmatrix} w=[111111]=[11][111]
而向量的外积运算本身也是一个卷积运算:
w = v w T = [ 1 1 ] ∗ [ 0 0 0 1 1 1 0 0 0 ] = [ 1 1 1 1 1 1 ] w=\mathbf{v}\mathbf{w}^T=\begin{bmatrix}1\\1\end{bmatrix}*\begin{bmatrix}0&0&0\\1&1&1\\0&0&0\end{bmatrix}=\begin{bmatrix}1&1&1\\1&1&1\end{bmatrix} w=vwT=[11]∗ 010010010 =[111111]
可分离核优势体现在计算上:
对于 M × N M\times N M×N的图像和大小 m × n m\times n m×n大小的核,卷积或者相关要 M N m n MNmn MNmn次乘法和加法,而对于可分离核,使用卷积交换律和结合律:
w ⋆ f = ( w 1 ⋆ w 2 ) ⋆ f = ( w 1 ⋆ f ) ⋆ w 2 w\star f=(w_1\star w_2)\star f=(w_1\star f)\star w_2 w⋆f=(w1⋆w2)⋆f=(w1⋆f)⋆w2
第一次运算需要 M N m MNm MNm次乘法和加法,第二次需要 M N n MNn MNn次乘法和加法,共需 M N ( m + n ) MN(m+n) MN(m+n)次乘法和加法。在线代中已经学过,判断是否可分离,就是判断矩阵的秩是否为1。
低通(平滑)滤波器
平滑,也称平均滤波器用于降低灰度的急剧过渡。由于噪声通常是急剧过渡的,因此,低通滤波器一个作用就是降噪;除此之外,低通滤波器还可以减少无关细节,无关细节指的是小于滤波器核的区域。同时,一些高通滤波器,带通滤波器和带阻滤波器也依赖于低通滤波器。
盒式滤波器核
之所以叫盒式核是因为以三维的方式看这些核就像盒子一样。其由元素为1的 m × n m\times n m×n阵列构成,前面跟一个归一化常数,是1除以系数和,一般系数为1,该常数就是 1 / m n 1/mn 1/mn。
这样做有两个目的:
- 低通滤波,滤波后像素值等于自己与周围像素值的均值。
- 避免在滤波过程中隐入偏差,也就是说原图像和滤波后图像像素值之和相同。
1 9 [ 1 1 1 1 1 1 1 1 1 ] \dfrac{1}{9}\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix} 91 111111111
3x3盒式平滑核,该核可分离且中心对称,因此相关运算等同于卷积。

左上为原图,右上为使用3x3平滑盒滤波结果,左下11x11,右下21x21。可以看出,11,21平滑盒卷积后边缘效应比较明显,这是0填充的后果。
代码:
function [out] = BoxFiltering(img, m)
%function [out] = BoxFiltering(img, m),m是滤波器核的大小,针对灰度图
filter = 1 / (m^2) * ones(m,m);
%filter = fspecial('average', m)
out = uint8(imfilter(img,filter,'conv','same'));
imfilter函数
g = imfilter(f, w, filtering_mode, boundary_options, size_options)
filtering_mode:可选’corr’,‘conv’,corr表示相关运算,conv表示卷积运算。
boundary_options:哎,现在不说,气不气。
size_options:可选’same’,‘full’,same表示输出图像大小与输出相同,从卷积核的中心和输入图像重合开始,像上上图。而full表示卷积核的右下角和图形开始重合就开始卷积,输出图像会比输入图像大,一般就用same。
低通高斯滤波器核
盒式核是比较简单的低通滤波器,但是它有很多局限性,比如其不能很好的近似透镜模糊特性,盒式滤波器会在垂直方向上进行模糊,但是其不具备各向同性(图像是二维的,方向有很多),在现实应用中使用的核通常是圆对称的(与方向无关),高斯核:
w ( s , t ) = G ( s , t ) = K e − s 2 + t 2 2 σ 2 = K e − r 2 2 σ 2 w(s,t)=G(s,t)=Ke^{-\dfrac{s^2+t^2}{2\sigma^2}}=Ke^{-\dfrac{r^2}{2\sigma^2}} w(s,t)=G(s,t)=Ke−2σ2s2+t2=Ke−2σ2r2
其中,r是 ( s , t ) (s,t) (s,t)到核中心的距离。
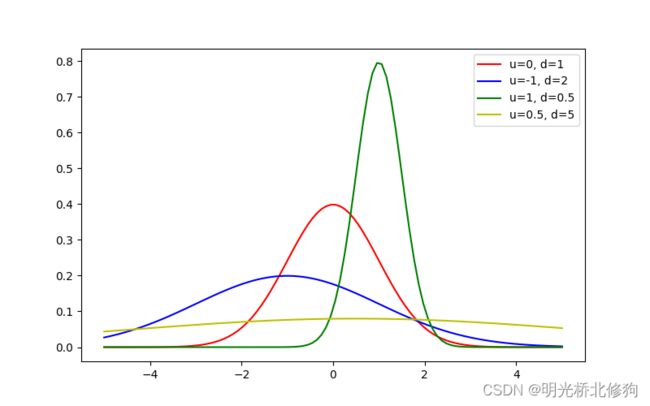
还记得高斯分布函数:
取一个方向 3 σ 3\sigma 3σ的积分就和整个分布函数的积分差不多了,所以,高斯核的大小有差不多 6 σ × 6 σ 6\sigma\times6\sigma 6σ×6σ效果就很好了,一般选择 m = ⌈ 6 σ ⌉ m=\lceil6\sigma\rceil m=⌈6σ⌉且m为奇数,比如 σ = 7 \sigma=7 σ=7, ⌈ 6 × 7 ⌉ = 42 \lceil6\times7\rceil=42 ⌈6×7⌉=42,核大小就是 43 × 43 43\times43 43×43。小的高斯核不具有高斯分布函数的钟形性质,更像盒式核。高斯函数有很多性质,比如两个高斯函数的乘积仍是高斯函数,两个高斯函数的卷积仍是高斯函数:
| f f f | g g g | f × g f\times g f×g | f ⋆ g f\star g f⋆g | |
|---|---|---|---|---|
| 均值 | m f m_f mf | m g m_g mg | m f × g = m f σ g 2 + m g σ f 2 σ f 2 + σ g 2 m_{f\times g}=\dfrac{m_f\sigma_g^2+m_g\sigma_f^2}{\sigma_f^2+\sigma_g^2} mf×g=σf2+σg2mfσg2+mgσf2 | m f ⋆ g = m f + m g m_{f\star g}=m_f+m_g mf⋆g=mf+mg |
| 标准差 | σ f \sigma_f σf | σ g \sigma_g σg | σ f × g = σ f 2 σ g 2 σ f 2 + σ g 2 \sigma_{f\times g}=\sqrt{\dfrac{\sigma_f^2\sigma_g^2}{\sigma_f^2+\sigma_g^2}} σf×g=σf2+σg2σf2σg2 | σ f ⋆ g = σ f 2 + σ g 2 \sigma_{f\star g}=\sqrt{\sigma_f^2+\sigma_g^2} σf⋆g=σf2+σg2 |
左图为原图,中图是 σ = 3.5 \sigma=3.5 σ=3.5的高斯核滤波后的图像,选 σ = 3.5 \sigma=3.5 σ=3.5是因为 6 × 3.5 = 21 6\times3.5=21 6×3.5=21,与之前盒式 m = 21 m=21 m=21进行类比,发现其模糊效果远比盒式核小,右图是 σ = 7 \sigma=7 σ=7的效果,发现这样才和盒式核 m = 21 m=21 m=21时差不多。
之前说取 6 σ 6\sigma 6σ就差不多,现在做一个验证,取 σ = 7 \sigma=7 σ=7,核大小分别取 43 × 43 43\times43 43×43和 85 × 85 85\times85 85×85:
左边两图像分别是核 43 × 43 , 85 × 85 43\times43,85\times85 43×43,85×85,右图是差值图像,差值最大值不足1,所以 ⌈ 6 σ ⌉ \lceil6\sigma\rceil ⌈6σ⌉就够用了。
function [out] = GaussianFiltering(img, sigma)
%function [out] = GaussianFiltering(img, sigma)
if mod(6*sigma,2)==0
m = 6*sigma+1;
else
m = 6*sigma;
end
filter = fspecial('gaussian', [m,m], sigma);
out = uint8(imfilter(img, filter, 'conv', 'same'));
fspecial函数
fspecial函数用于生成滤波器核
h = fspecial(type)
h = fspecial('average',hsize)
h = fspecial('disk',radius)
h = fspecial('gaussian',hsize,sigma)
h = fspecial('laplacian',alpha)
h = fspecial('log',hsize,sigma)
h = fspecial('motion',len,theta)
h = fspecial('prewitt')
h = fspecial('sobel')
这里用的高斯核hsize是核的大小,用一个向量定义,sigma是标准差。
两种平滑核的比较
左图是21x21盒式核的平滑结果,右图是 σ = 7 \sigma=7 σ=7,43x43平滑盒的平滑结果。发现盒式平滑中 a \mathbf{a} a没有高斯平滑的平滑。

分别是原图,盒式核滤波,高斯核滤波的结果。盒式核在边缘开始处和结束处都是硬过渡的。
填充策略
-
0填充(zero padding)
在图像四周补0就完事了
-
复制填充(replication padding)
用图像最邻近的边界像素值填充,要填充多行多列时还用这个值
-
镜像填充(reflection padding)
用图像的镜像填充
一般来说,处理单张图不使用0填充,,如果图像边界几层值相同(边框附近区域值相同),使用复制填充就可以,如果边框附近几层有细节,使用镜像填充比较好。
左图0填充,中图复制填充,右图镜像填充,右边两个消除了边框的黑色。
g = imfilter(f, w, filtering_mode, boundary_options, size_options)
boundary_options就是选择填充策略的:不传值就是0填充,replicate复制填充,symmetric镜像填充,circular周期填充。
一些应用
- 提取RoI
左图是哈勃望远镜拍摄的星系图,中图使用 σ = 17 \sigma=17 σ=17的高斯核平滑,右图使用 T = 0.2 T=0.2 T=0.2的阈值进行二值化中图得到RoI。
-
阴影矫正(平坦场矫正)
阴影由光照不均造成,对后续的自动化图像处理算法结果影响很大(比如目标检测)。使用滤波的方法矫正比较简单快速,当然,也很初级。
中图是左图的高斯平滑结果,右图用左图除以中图得到。
统计排序(非线性)滤波
统计排序滤波依赖对滤波器核中像素值的排序,比如中值滤波器,用滤波器核中的像素值的种植代替计算的像素点的像素值。
当图像存在冲激噪声(也叫椒盐噪声,因为像椒盐)时,中值滤波器很好用。中值滤波器的作用是使每个像素点更像其周围的像素点。
左图为原图,中图为 σ = 3 \sigma=3 σ=3的高斯核低通滤波降噪,右图为7x7中值滤波降噪。
高通(锐化)滤波器
之前说的,高频再图像中对应的使边缘、细节、噪声。在离散函数中,求平均和积分类似,微分和求导类似。这里通过空间微分实现高通滤波。
数字函数的导数由差分定义:
-
一阶导
∂ f ∂ x = f ( x + 1 ) + f ( x ) \dfrac{\partial{f}}{\partial{x}}=f(x+1)+f(x)\\ ∂x∂f=f(x+1)+f(x) -
二阶导
∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \dfrac{\partial^2{f}}{\partial{x^2}}=f(x+1)+f(x-1)-2f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)
假设有一条扫描线
6 6 6 6 5 4 3 2 1 1 1 1 1 1 6 6 6 6 6 \begin{matrix}6&6&6&6&5&4&3&2&1&1&1&1&1&1&6&6&6&6&6 \end{matrix} 6666543211111166666
一阶导
0 0 − 1 − 1 − 1 − 1 − 1 0 0 0 0 0 5 0 0 0 0 \begin{matrix}0&0&-1&-1&-1&-1&-1&0&0&0&0&0&5&0&0&0&0\end{matrix} 00−1−1−1−1−10000050000
二阶导
0 0 − 1 0 0 0 0 1 0 0 0 0 5 − 5 0 0 0 \begin{matrix}0&0&-1&0&0&0&0&1&0&0&0&0&5&-5&0&0&0\end{matrix} 00−10000100005−5000
可以看出,二阶导能更好的反应边缘,是锐化图像的一个好的特性。
拉普拉斯----二阶导锐化图像
最简单的各向同性导数算子是拉普拉斯,定义为
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^2f=\dfrac{\partial^2f}{\partial{x^2}}+\dfrac{\partial^2f}{\partial{y^2}} ∇2f=∂x2∂2f+∂y2∂2f
因为这里的数字函数的导数是线性运算,所以这里的拉普拉斯也是线性算子(和拉普拉斯变换不是一个东西)。
在x方向:
∂ 2 f ∂ x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) \dfrac{\partial^2f}{\partial{x^2}}=f(x+1,y)+f(x-1,y)-2f(x,y) ∂x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)
在y方向:
∂ 2 f ∂ x 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \dfrac{\partial^2f}{\partial{x^2}}=f(x,y+1)+f(x,y-1)-2f(x,y) ∂x2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)
那么,两个变量的离散拉普拉斯是
∇ 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
同样,也可以使用卷积实现
[ 0 1 0 1 − 4 1 0 1 0 ] [ 1 1 1 1 − 8 1 1 1 1 ] [ 0 − 1 0 − 1 4 − 1 0 − 1 0 ] [ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] \begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{bmatrix} \begin{bmatrix} 1&1&1\\ 1&-8&1\\1&1&1 \end{bmatrix} \begin{bmatrix} 0&-1&0\\ -1&4&-1\\ 0&-1&0 \end{bmatrix} \begin{bmatrix} -1&-1&-1\\ -1&8&-1\\ -1&-1&-1 \end{bmatrix} 0101−41010 1111−81111 0−10−14−10−10 −1−1−1−18−1−1−1−1
左一的核是xy两个方向上的二阶导。左二的核加入了主对角线和副对角线的二阶导。
后面两个作为补充,只是对前两个核取负值,有利于后面的计算。
经过这个卷积运算提取高频的细节核边缘,经过和原图的加和就可以锐化图像:
g ( x , y ) = f ( x , y ) + c [ ∇ 2 f ( x , y ) ] g(x,y)=f(x,y)+c[\nabla^2f(x,y)] g(x,y)=f(x,y)+c[∇2f(x,y)]
对于前两个核 c = − 1 c=-1 c=−1,对于后两个核 c = 1 c=1 c=1。
左上图为原图,右上图为使用第一个拉普拉斯算子得到的拉普拉斯图像,图三是前两张图像的和形成的锐化图像,图四是对左下图使用第拉普拉斯算子在与左下图相加得到的锐化图像。
可以看到,每个核的和都是0,那么,在灰度恒定处运算结果都是0。虽然这样不会引入偏差,但是在有些地方运算会产生负值(截断为0),这样就会引入偏差,导致视觉效果不好,需要额外的处理。
钝化掩蔽和高提升滤波
钝化掩蔽的过程
- 模糊原图
- 用原图减去模糊后的图像得到模板(mask)
- 将原图和模板相加
令 f ( x , y ) ‾ \overline{f(x,y)} f(x,y)表示图像的模糊,模板为
g m a s k ( x , y ) = f ( x , y ) − f ( x , y ) ‾ g_{mask}(x,y)=f(x,y)-\overline{f(x,y)} gmask(x,y)=f(x,y)−f(x,y)
再将原图和加权模板相加
g ( x , y ) = f ( x , y ) + k g m a s k ( x , y ) g(x,y)=f(x,y)+kg_{mask}(x,y) g(x,y)=f(x,y)+kgmask(x,y)
其中 k ( k ⩾ 0 ) k(k\geqslant0) k(k⩾0), k = 0 k=0 k=0时称为钝化掩蔽, k > 1 k>1 k>1时称为高提升滤波。

第一行三张图分别是原图,模糊后的图像,模板。
第二行三张图分别是钝化掩蔽,k=2高提升滤波,k=3高提升滤波。
通常,只要模板中的东西还能被人分辨,参数就不重要。
一阶导求梯度锐化图像
数字函数的梯度定义如下:
∇ f ≡ g r a d ( f ) = [ g x g y ] = [ ∂ f / ∂ x ∂ f / ∂ y ] \nabla f\equiv grad(f)=\begin{bmatrix}g_x\\g_y\end{bmatrix}=\begin{bmatrix}\partial f/\partial x\\\partial f/\partial y\end{bmatrix} ∇f≡grad(f)=[gxgy]=[∂f/∂x∂f/∂y]
表示f的最大变化率。
其量 M ( x , y ) M(x,y) M(x,y)(Magnitude)可以是
M ( x , y ) = ∣ ∣ ∇ f ∣ ∣ = g x 2 + g y 2 M(x,y)=\vert\vert\nabla f\vert\vert=\sqrt {g_x^2+g_y^2} M(x,y)=∣∣∇f∣∣=gx2+gy2
有些时候使用L1范数更合适
M ( x , y ) ≈ ∣ g x ∣ + ∣ g y ∣ M(x,y)\approx \vert g_x\vert+\vert g_y\vert M(x,y)≈∣gx∣+∣gy∣
求一阶导的运算是线性的,但是求梯度因为有平方,开方或者绝对值,所以这个运算不是线性的。
假设一般的3x3滤波器核有如下形式
[ z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 ] \begin{bmatrix} z_1&z_2&z_3\\ z_4&z_5&z_6\\ z_7&z_8&z_9 \end{bmatrix} z1z4z7z2z5z8z3z6z9
Roberts算子
1965年由Roberts提出,使用交叉差值计算主副对角线的梯度:
d x = [ − 1 0 0 1 ] d y = [ 0 − 1 1 0 ] d_x=\begin{bmatrix} -1&0\\ 0&1 \end{bmatrix}\qquad d_y=\begin{bmatrix} 0&-1\\ 1&0 \end{bmatrix} dx=[−1001]dy=[01−10]
那么,根据上述滤波器核的形式
g x = z 9 − z 5 g y = z 8 − z 6 g_x=z_9-z_5\\ g_y=z_8-z_6 gx=z9−z5gy=z8−z6
计算的时候用的是
d x = [ 0 0 0 0 − 1 0 0 0 1 ] d y = [ 0 0 0 0 0 − 1 0 1 0 ] d_x=\begin{bmatrix} 0&0&0\\ 0&-1&0\\ 0&0&1 \end{bmatrix}\qquad d_y=\begin{bmatrix} 0&0&0\\ 0&0&-1\\ 0&1&0 \end{bmatrix} dx= 0000−10001 dy= 0000010−10
因为滤波器核一般是奇数大小,这样才能确定一个核的中心点。
Sobel算子
d x = [ − 1 − 2 − 1 0 0 0 1 2 1 ] d y = [ − 1 0 1 − 2 0 2 1 0 1 ] d_x=\begin{bmatrix} -1&-2&-1\\ 0&0&0\\ 1&2&1 \end{bmatrix}\qquad d_y=\begin{bmatrix} -1&0&1\\ -2&0&2\\ 1&0&1 \end{bmatrix} dx= −101−202−101 dy= −1−21000121
2而不是1是因为,这样做有一定的平滑抗噪效果,边缘探测和图像分割章节中会具体讨论。

左上图为原图,右上图为Roberts+L2范数锐化的图像,左下图为Roberts+L1范数锐化的图像,由下图为Sobel算子+L2范数锐化的图像。
Roberts:
function [out] = RobertGradient(img, mode)
%function [out] = RobertEdge(img, mode),mode可以是square也可以是absolute
dx = [-1,0;0,1];
dy = [0,-1;1,0];
imgx = im2double(imfilter(img, dx, 'corr', 'same'));
imgy = im2double(imfilter(img, dy, 'corr', 'same'));
[M,N] = size(img);
out = zeros(M,N);
if strcmp(mode, 'square')
for i=1:M
for j=1:N
out(i,j)=sqrt(imgx(i,j)^2+imgy(i,j)^2);
end
end
end
if strcmp(mode, 'absolute')
for i=1:M
for j=1:N
out(i,j)=abs(imgx(i,j))+abs(imgy(i,j));
end
end
end
out = im2uint8(out);
Sobel:
function [out] = SobelGradient(img)
%function [out] = SobelGradient(img)
dx = [-1,-2,-1;0,0,0;1,2,1];
dy = [-1,0,1;-2,0,2;-1,0,1];
imgx = im2double(imfilter(img,dx,'corr','same'));
imgy = im2double(imfilter(img,dy,'corr','same'));
[M,N] = size(img);
out = zeros(M,N);
for i=1:M
for j=1:N
out(i,j) = sqrt(imgx(i,j)^2+imgy(i,j)^2);
end
end
out = im2uint8(out);
低通,高通,带通和带阻滤波器
前面说过,可以利用低通滤波器构建高通滤波器,带通和带阻滤波器。
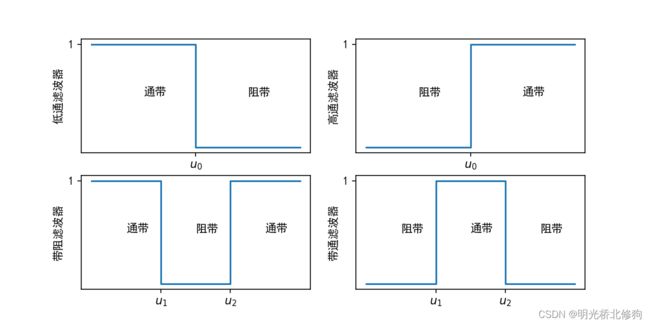
如上图,是在频域各种滤波器的表现,在频率中用1减去低通滤波器就是高通滤波器,频域中的1在空间域中是单位冲激信号,从单位冲激信号中减去一个低通滤波器核就会得到一个高通滤波器和,用这个滤波器核对图像滤波的结果和从原图中减去低通滤波的结果是相同的,钝化掩蔽就是用的这个,证明:
钝化掩蔽图像:
g ( x , y ) = f ( x , y ) + k [ f ( x , y ) − f ( x , y ) ‾ ] g(x,y)=f(x,y)+k[f(x,y)-\overline{f(x,y)}] g(x,y)=f(x,y)+k[f(x,y)−f(x,y)]
拉普拉斯图像:
∇ 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
原图减去拉普拉斯图像:
f ( x , y ) − ∇ 2 f ( x , y ) = f ( x , y ) − [ f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) ] = 6 f ( x , y ) − [ f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) + f ( x , y ) ] = 5 { 1.2 f ( x , y ) − 1 5 [ f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) + f ( x , y ) ] } = 5 [ 1.2 f ( x , y ) − f ( x , y ) ‾ ] f(x,y)-\nabla^2f(x,y)=\\ f(x,y)-[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)]=\\ 6f(x,y)-[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)+f(x,y)]=\\ 5\{1.2f(x,y)-\dfrac{1}{5}[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)+f(x,y)]\}=\\ 5[1.2f(x,y)-\overline{f(x,y)}] f(x,y)−∇2f(x,y)=f(x,y)−[f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)]=6f(x,y)−[f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)+f(x,y)]=5{1.2f(x,y)−51[f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)+f(x,y)]}=5[1.2f(x,y)−f(x,y)]
原图减去拉普拉斯图像和钝化掩蔽的图像成正比,即证。
组合使用空间增强方法
图a,原图,人体骨骼扫描图像,这副图像有很多噪声,动态范围狭窄,需要突出骨骼的细节。
策略:
- 拉普拉斯突出细节
- 梯度突出边缘
- 平滑降噪图像来掩蔽拉普拉斯图像
- 灰度变换拉伸动灰度级来扩大动态范围
图b。原图的拉普拉斯图像,将处理的后的图像灰度值0调成了127,不然不好看出来。

图c,图a减去图b得到的锐化图像。虽然骨骼轮廓更加明显了,但是噪声也被放大了。
图d,原图的Sobel图像。
图e,对图d施加了一个5x5盒式滤波。
图f,图b和图e相乘得到的mask。
图g,图a加上图f的mask。
图h,对图g施加了一个幂律变换拉伸对比度。