FCN网络结构解析

daily：作为深度学习图片分割第一个学习的网络结构

Q1： 为什么要用FCN？

A1：应为和以前网络R-CNN，SDS相比提升比较大

Q2：与CNN什么区别？

A2:使用全卷积层代替全连接层

Q3：为什么要进行代替？

A3：1.全连接层训练时输入节点个数是固定的，如果输入节点发生变化就会报错（以后解决了），使用全卷积代替全连接层可以不用对于图片大小做规定。

        2.如果使用全连接层结果是一个柱状图的形式（向量），但是使用全卷积代替全连接得到的结果是一个2D的形式，可以将其可视化为一个heatmap形式。

 Q4：如何将全连接替换成全卷积(论文中，达到最高精度的分类网络是VGG16，但提供的模型基于AlexNet)

   全连接层和卷积层之间唯一的不同就是卷积层中的神经元只与输入数据中的一个局部区域连接，并且在卷积列中的神经元共享参数。然而在两类层中，神经元都是计算点积，所以它们的函数形式是一样的。因此，将此两者相互转化是可能的：
   （1）对于任一个卷积层，都存在一个能实现和它一样的前向传播函数的全连接层。权重矩阵是一个巨大的矩阵，除了某些特定块，其余部分都是零。而在其中大部分块中，元素都是相等的。
   （2）任何全连接层都可以被转化为卷积层。比如VGG16中第一个全连接层是25088 * 4096的数据尺寸，将它转化为512 * 7 * 7 * 4096的数据尺寸，即一个K=4096的全连接层，输入数据体的尺寸是7 * 7 * 512，这个全连接层可以被等效地看做一个F=7, P=0, S=1, K=4096 的卷积层。换句话说，就是将滤波器的尺寸设置为和输入数据体的尺寸一致7 * 7, 这样输出就变为1 * 1 * 4096, 本质上和全连接层的输出是一样的。
   输出激活数据体深度是由卷积核的数目决定的(K=4096)。
   在两种变换中，将全连接层转化为卷积层在实际运用中更加有用。假设一个卷积神经网络的输入是227x227x3的图像，一系列的卷积层和下采样层将图像数据变为尺寸为7x7x512的激活数据体, AlexNet的处理方式为使用了两个尺寸为4096的全连接层，最后一个有1000个神经元的全连接层用于计算分类评分。我们可以将这3个全连接层中的任意一个转化为卷积层：
   （1）第一个连接区域是[7x7x512]的全连接层，令其滤波器尺寸为F=7,K=4096，这样输出数据体就为[1x1x4096]。
   （2）第二个全连接层，令其滤波器尺寸为F=1,K=4096，这样输出数据体为[1x1x4096]。
   （3）最后一个全连接层也做类似的，令其F=1,K=1000，最终输出为[1x1x1000]。

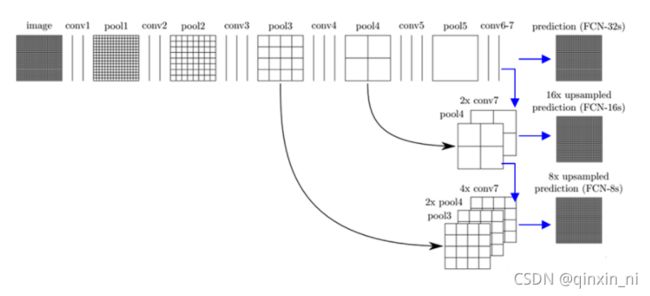
Q5: FCN-32s,FCN-16s,FCN-8s有什么区别?

A5:FCN-32S就是上采样32倍，FCN16s就是上采样16倍，FCN-8s就是上采样8倍，所以FCN-8s效果更好

Q6:为什么传统CNN的输入图片是固定大小？

A6:对于CNN，一幅输入图片在经过卷积和pooling层时，这些层是不关心图片大小的。比如对于一个卷积层，outputsize = (inputsize - kernelsize) / stride + 1，它并不关心inputsize多大，对于一个inputsize大小的输入feature map，滑窗卷积，输出outputsize大小的feature map即可。pooling层同理。但是在进入全连接层时，feature map（假设大小为n×n）要拉成一条向量，而向量中每个元素（共n×n个）作为一个结点都要与下一个层的所有结点（假设4096个）全连接，这里的权值个数是4096×n×n，而我们知道神经网络结构一旦确定，它的权值个数都是固定的，所以这个n不能变化，n是conv5的outputsize，所以层层向回看，每个outputsize都要固定，那每个inputsize都要固定，因此输入图片大小要固定。

Q8:把全连接层的权重W重塑成卷积层的滤波器有什么好处？

A8:这样的转化可以在单个向前传播的过程中, 使得卷积网络在一张更大的输入图片上滑动，从而得到多个输出(可以理解为一个label map)。
   比如: 我们想让224×224尺寸的浮窗，以步长为32在384×384的图片上滑动，把每个经停的位置都带入卷积网络，最后得到6×6个位置的类别得分, 那么通过将全连接层转化为卷积层之后的运算过程为:
   如果224×224的输入图片经过卷积层和下采样层之后得到了[7x7x512]的数组，那么，384×384的大图片直接经过同样的卷积层和下采样层之后会得到[12x12x512]的数组, 然后再经过上面由3个全连接层转化得到的3个卷积层，最终得到[6x6x1000]的输出((12 – 7)/1 + 1 = 6), 这个结果正是浮窗在原图经停的6×6个位置的得分。
   一个确定的CNN网络结构之所以要固定输入图片大小，是因为全连接层权值数固定，而该权值数和feature map大小有关, 但是FCN在CNN的基础上把1000个结点的全连接层改为含有1000个1×1卷积核的卷积层，经过这一层，还是得到二维的feature map，同样我们也不关心这个feature map大小, 所以对于输入图片的size并没有限制。

FCN流程

原理：FCN将传统卷积网络后面的全连接层换成了卷积层，这样网络输出不再是类别而是 heatmap；同时为了解决因为卷积和池化对图像尺寸的影响，提出使用上采样的方式恢复。

 

 1.卷积：

以原图像进行卷积conv1、pool1后原图像缩小为1/2；之后对图像进行第二次conv2、pool2后图像缩小为1/4；接着继续对图像进行第三次卷积操作conv3、pool3缩小为原图像的1/8，此时保留pool3的featureMap；接着继续对图像进行第四次卷积操作conv4、pool4，缩小为原图像的1/16，保留pool4的featureMap；最后对图像进行第五次卷积操作conv5、pool5，缩小为原图像的1/32，

2.全卷积：

然后把原来CNN操作中的全连接变成卷积操作conv6、conv7，图像的featureMap数量改变但是图像大小依然为原图的1/32，此时图像不再叫featureMap而是叫heatMap。

 3.上采样：

现在我们有1/32尺寸的heatMap，1/16尺寸的featureMap和1/8尺寸的featureMap，1/32尺寸的heatMap进行upsampling（上采样）操作之后，因为这样的操作还原的图片仅仅是conv5中的卷积核中的特征，限于精度问题不能够很好地还原图像当中的特征，因此在这里向前迭代。把conv4中的卷积核对上一次upsampling之后的图进行反卷积补充细节（相当于一个差值过程），最后把conv3中的卷积核对刚才upsampling之后的图像进行再次反卷积补充细节，最后就完成了整个图像的还原。

notes:上采样upsample

图像上采样upsampling的主要目的是放大图像，主要包括：

（1）几乎都是采用内插值法，即在原有图像像素的基础上，在像素点值之间采用合适的插值算法插入新的元素；

（2）反卷积方法（Deconvolution），又称转置卷积法(Transposed Convolution)；

（3）反池化方法（Unpooling）。

详情见：图像上采样--双线性插值_qinghuaci666的博客-CSDN博客_双线性采样

 4.跳跃结构：

对第5层的输出执行32倍的反卷积得到原图，得到的结果不是很精确，论文中同时执行了第4层和第3层输出的反卷积操作（分别需要16倍和8倍的上采样），再把这3个反卷积的结果图像融合，提升了结果的精确度：

FNC模型实现过程：

用AlexNet，VGG16或者GoogleNet训练好的模型做初始化，在这个基础上做fine-tuning，全部都fine-tuning，只需在末尾加上upsampling，参数的学习还是利用CNN本身的反向传播原理。
   （2）采用whole image做训练，不进行patchwise sampling。实验证明直接用全图已经很effective and efficient。
   （3）对class score的卷积层做全零初始化。随机初始化在性能和收敛上没有优势。
举例：
   FCN例子: 输入可为任意尺寸图像彩色图像；输出与输入尺寸相同，深度为：20类目标+背景=21，模型基于AlexNet。
   蓝色：卷积层。
   绿色：Max Pooling层。
   黄色: 求和运算, 使用逐数据相加，把三个不同深度的预测结果进行融合：较浅的结果更为精细，较深的结果更为鲁棒。
   灰色: 裁剪, 在融合之前，使用裁剪层统一两者大小, 最后裁剪成和输入相同尺寸输出。
   对于不同尺寸的输入图像，各层数据的尺寸（height，width）相应变化，深度（channel）不变。

 （1）全卷积层部分进行特征提取, 提取卷积层（3个蓝色层）的输出来作为预测21个类别的特征。

 （2）图中虚线内是反卷积层的运算, 反卷积层（3个橙色层）可以把输入数据尺寸放大。和卷积层一样，升采样的具体参数经过训练确定。

    

        1.以经典的AlexNet分类网络为初始化。最后两级是全连接（红色），参数弃去不用。

  2.从特征小图（蓝色）预测分割小图（橙色），之后直接升采样为大图。

反卷积（橙色）的步长为32，这个网络称为FCN-32s

   3.升采样分为两次完成（橙色×2）, 在第二次升采样前，把第4个pooling层（绿色）的预测结果（蓝色）融合进来。使用跳级结构提升精确性。

第二次反卷积步长为16，这个网络称为FCN-16s

   4. 升采样分为三次完成（橙色×3）, 进一步融合了第3个pooling层的预测结果。

第三次反卷积步长为8，记为FCN-8s

• 其他参数: minibatch：20张图片。   
• learning rate：0.001。   
• 初始化：分类网络之外的卷积层参数初始化为0。   
• 反卷积参数初始化为bilinear插值。   
• 最后一层反卷积固定位bilinear插值不做学习。

 FCN缺点

   （1）得到的结果还是不够精细。进行8倍上采样虽然比32倍的效果好了很多，但是上采样的结果还是比较模糊和平滑，对图像中的细节不敏感。
   （2）对各个像素进行分类，没有充分考虑像素与像素之间的关系。忽略了在通常的基于像素分类的分割方法中使用的空间规整（spatial regularization）步骤，缺乏空间一致性。

BTY:部分转载于DeepLearning-500-questions