Python实现粒子群算法（PSO）+支持向量回归机（SVR）的时间序列预测

本实验使用环境为Anaconda3 Jupyter，调用Sklearn包，请提前准备好。

1.引入一些常见包

import csv
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from datetime import datetime 
from sklearn.metrics import explained_variance_score
from sklearn.svm import SVR 
from sklearn.metrics import mean_squared_error 
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import explained_variance_score
from sklearn import metrics
from sklearn.metrics import mean_absolute_error # 平方绝对误差
import random

2.引入数据

将准备好的CSV文件导入，将数据分为目标集和特征集，本文预测溶解氧。由于是时间序列预测，所以目标集和特征集需要需要反转。

#时间
time=[]
#特征
feature=[]
#目标
target=[]

csv_file = csv.reader(open('南沙水质数据.csv'))
for content in csv_file:
    content=list(map(float,content))
    if len(content)!=0:
        feature.append(content[1:4])
        target.append(content[0:1])

csv_file = csv.reader(open('南沙水质时间.csv'))
for content in csv_file:
    content=list(map(str,content))
    if len(content)!=0:
        time.append(content)
        
targets=[]
for i in target:
    targets.append(i[0])
 
feature.reverse()
targets.reverse()

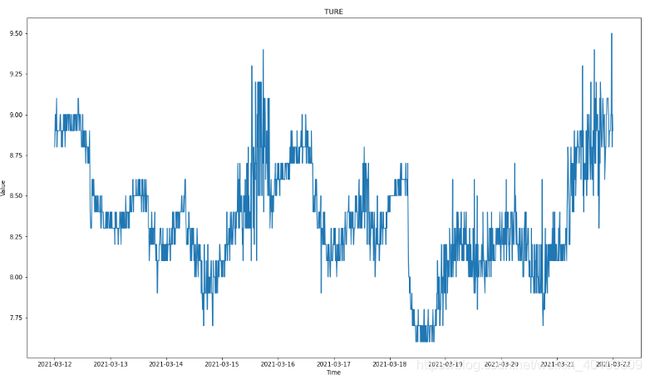
调整时间日期的格式，画出溶解氧数据的变化图。

#str转datetime
time_rel=[]
for i,j in enumerate(time):
    time_rel.append(datetime.strptime(j[0],'%Y/%m/%d %H:%M'))
time_rel.reverse()

fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title('TURE')
plt.plot(time_rel, targets)
plt.xlabel('Time')
plt.ylabel('Value')

结果如下：

3.数据标准化

使用StandardScaler()方法将特征数据标准化归一化。

# 标准化转换
scaler = StandardScaler()
# 训练标准化对象
scaler.fit(feature)
# 转换数据集
feature= scaler.transform(feature)

4.使用支持向量回归机（SVR）

先将数据随机90%做测试集，剩下10%当验证集，随机种子任意设置。本文采取时间序列预测，将特征集和目标集的后10%留出来，做为验证集并覆盖之前的验证值。

feature_train, feature_test, target_train, target_test = train_test_split(feature, targets, test_size=0.1,random_state=8)

feature_test=feature[int(len(feature)*0.9):int(len(feature))]
target_test=targets[int(len(targets)*0.9):int(len(targets))]
label_time=time_rel[int(len(time_rel)*0.9):int(len(time_rel))]

model_svr = SVR(C=1,epsilon=0.1,gamma=10)
model_svr.fit(feature_train,target_train)
predict_results=model_svr.predict(feature_test)
plt.plot(label_time,target_test)#测试数组
plt.plot(label_time,predict_results)#测试数组
plt.legend(['True','SVR'])
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("SVR")  # 标题
plt.show()
print("MSE:",mean_squared_error(target_test,predict_results))
print("R2 = ",metrics.r2_score(target_test,predict_results)) # R2
print("MAE = ",mean_absolute_error(target_test,predict_results)) # R2

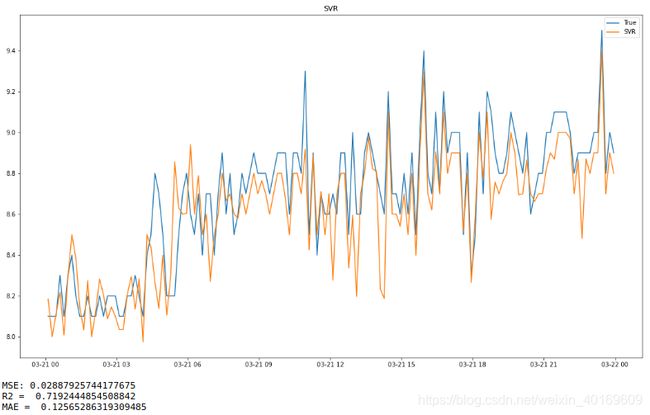
最终结果如下：
精度过低，需要使用优化算法进行优化，本文选择PSO。

5.使用PSO算法对SVR进行调参

对SVR参数的惩罚参数C、损失函数epsilon、核系数gamma进行调参，设置其范围为[0,10]、[0,5]、[0,100]，可以自行设置。一共20代，每代20人，可以自行设置。

class PSO:
    def __init__(self, parameters):
        """
        particle swarm optimization
        parameter: a list type, like [NGEN, pop_size, var_num_min, var_num_max]
        """
        # 初始化
        self.NGEN = parameters[0]    # 迭代的代数
        self.pop_size = parameters[1]    # 种群大小
        self.var_num = len(parameters[2])     # 变量个数
        self.bound = []                 # 变量的约束范围
        self.bound.append(parameters[2])
        self.bound.append(parameters[3])
 
        self.pop_x = np.zeros((self.pop_size, self.var_num))    # 所有粒子的位置
        self.pop_v = np.zeros((self.pop_size, self.var_num))    # 所有粒子的速度
        self.p_best = np.zeros((self.pop_size, self.var_num))   # 每个粒子最优的位置
        self.g_best = np.zeros((1, self.var_num))   # 全局最优的位置
 
        # 初始化第0代初始全局最优解
        temp = -1
        for i in range(self.pop_size):
            for j in range(self.var_num):
                self.pop_x[i][j] = random.uniform(self.bound[0][j], self.bound[1][j])
                self.pop_v[i][j] = random.uniform(0, 1)
            self.p_best[i] = self.pop_x[i]      # 储存最优的个体
            fit = self.fitness(self.p_best[i])
            if fit > temp:
                self.g_best = self.p_best[i]
                temp = fit
 
    def fitness(self, ind_var):
        X = feature_train
        y = target_train
        """
        个体适应值计算
        """
        x1 = ind_var[0]
        x2 = ind_var[1]
        x3 = ind_var[2]
        
        if x1==0:x1=0.001
        if x2==0:x2=0.001
        if x3==0:x3=0.001
            
        clf = SVR(C=x1,epsilon=x2,gamma=x3)
        clf.fit(X, y)
        predictval=clf.predict(feature_test)
        print("R2 = ",metrics.r2_score(target_test,predictval)) # R2
        return  metrics.r2_score(target_test,predictval)
 
    def update_operator(self, pop_size):
        """
        更新算子：更新下一时刻的位置和速度
        """
        c1 = 2     # 学习因子，一般为2
        c2 = 2
        w = 0.4    # 自身权重因子
        for i in range(pop_size):
            # 更新速度
            self.pop_v[i] = w * self.pop_v[i] + c1 * random.uniform(0, 1) * (
                        self.p_best[i] - self.pop_x[i]) + c2 * random.uniform(0, 1) * (self.g_best - self.pop_x[i])
            # 更新位置
            self.pop_x[i] = self.pop_x[i] + self.pop_v[i]
            # 越界保护
            for j in range(self.var_num):
                if self.pop_x[i][j] < self.bound[0][j]:
                    self.pop_x[i][j] = self.bound[0][j]
                if self.pop_x[i][j] > self.bound[1][j]:
                    self.pop_x[i][j] = self.bound[1][j]
            # 更新p_best和g_best
            if self.fitness(self.pop_x[i]) > self.fitness(self.p_best[i]):
                self.p_best[i] = self.pop_x[i]
            if self.fitness(self.pop_x[i]) > self.fitness(self.g_best):
                self.g_best = self.pop_x[i]
 
    def main(self):
        popobj = []
        self.ng_best = np.zeros((1, self.var_num))[0]
        for gen in range(self.NGEN):
            self.update_operator(self.pop_size)
            popobj.append(self.fitness(self.g_best))
            print('############ Generation {} ############'.format(str(gen + 1)))
            if self.fitness(self.g_best) > self.fitness(self.ng_best):
                self.ng_best = self.g_best.copy()
            print('最好的位置：{}'.format(self.ng_best))
            print('最大的函数值：{}'.format(self.fitness(self.ng_best)))
        print("---- End of (successful) Searching ----")
 
        plt.figure()
        fig = plt.gcf()
        fig.set_size_inches(18.5, 10.5)
        plt.title("Figure1")
        plt.xlabel("iterators", size=14)
        plt.ylabel("fitness", size=14)
        t = [t for t in range(self.NGEN)]
        plt.plot(t, popobj, color='b', linewidth=2)
        plt.show()

跑起来～

if __name__ == '__main__':
    NGEN = 20
    popsize = 20
    low = [0,0,0]
    up = [10,5,100]
    parameters = [NGEN, popsize, low, up]
    pso = PSO(parameters)
    pso.main()

最优适应值变化如下：

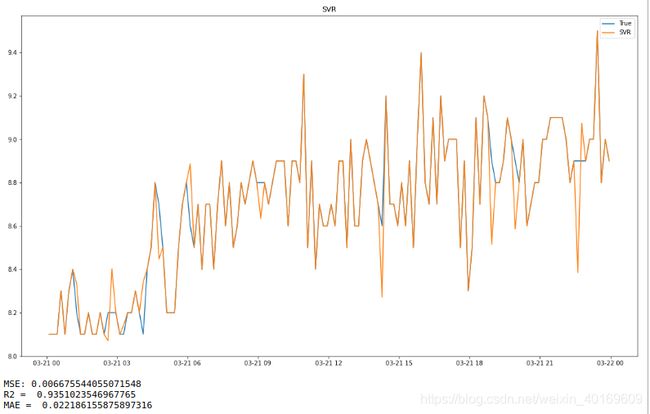
6.融合PSO-SVR模型

model_svr = SVR(C=10,epsilon=0,gamma=34.03015737)
model_svr.fit(feature_train,target_train)
predict_results=model_svr.predict(feature_test)
plt.plot(label_time,target_test)#测试数组
plt.plot(label_time,predict_results)#测试数组
plt.legend(['True','SVR'])
fig = plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.title("SVR")  # 标题
plt.show()
print("MSE:",mean_squared_error(target_test,predict_results))
print("R2 = ",metrics.r2_score(target_test,predict_results)) # R2
print("MAE = ",mean_absolute_error(target_test,predict_results)) # R2

结果如下：
其各项评价指标均变优