推荐系统学习笔记召回策略之基于协同过滤召回

图1. 推荐系统整体架构

---

推荐系统学习笔记系列链接：

推荐系统学习笔记——特征工程
推荐系统学习笔记召回策略之基于内容召回
推荐系统学习笔记召回策略之基于协同过滤召回
推荐系统召回策略之多路召回与Embedding召回

---

1. 概述

协同过滤算法在推荐系统界可谓是大名鼎鼎，甚至一度两者被划上等号。对协同过滤算法的研究最早可以追溯到1992年，Xerox开发出了一款基于协同过滤算法的邮件筛选软件，后来到了2003年，Amazon的一篇关于协同过滤的论文让其在互联网领域大放光彩，时至今日，关于协同过滤的研究已经与当前最热门的深度学习相结合，仍发挥着其不可替代的作用。基于协同过滤的推荐算法可以划分为两部分：

• 基于近邻的协同过滤
• 基于模型的协同过滤

其中基于近邻的协同过滤又可以被划分为：

• 基于用户的协同过滤（UserCF）
• 基于物品的协同过滤（ItemCF）

基于近邻的协同过滤算法是指记住每个用户消费过什么东西，然后推荐给他相似的物品（ItemCF）或者推荐与他有相似喜好的人所喜欢的东西（UserCF）。基于模型的协同过滤算法则是从用户和物品的关系矩阵中学习一个可以泛化的模型，从而将那些矩阵空白处填满。

当一个推荐系统度过了最初期的冷启动阶段后，就能够拥有了一定可观的用户行为了。这些用户行为或明或暗地表达了他们对一些物品的喜欢程度，这些行为可以构成一个用户与物品的关系矩阵（Matrix）。这个关于用户和物品的关系矩阵中填充的就是用户对物品的态度，但不一定每个位置都有内容，而我们需要做的就是把那些还没有内容的空格填充上。需要注意的是，这个关系矩阵是协同过滤算法的”命根子“，一切工作都围绕着这个关系矩阵来进行。 关系矩阵如下图所示：

	Item1	Item2	Item3	Item4	Item5	Item6	Item7
User1	1	1	?	?	1	?	0
User2	?	1	?	1	0	?	?
User3	1	0	1	?	?	?	1
User4	1	1	?	0	?	1	?
User5	?	?	1	?	1	?	0

图1 用户关系矩阵

2. 基于近邻的协同过滤算法

所谓的协同过滤算法，顾名思义，就是协同大家一起来对海量的信息进行处理过滤，从中筛选出目标用户可能感兴趣的信息的推荐过程。

1. 基于用户的协同过滤算法（UserCF）

基于用户的协同过滤算法听上去可能你会觉得很陌生，但是举个身边的例子你就会明白这个算法是用来干啥的了。比如说你刚上研究生去实验室的时候你可能会问你的师兄师姐们应该买什么书籍，读什么论文，这个时候师兄师姐们就会给你一些关于书籍和论文的推荐。在这个例子中，你可能会问很多师兄师姐，他们都给了你一些推荐，你在其中做选择的时候很大概率会选择跟你研究方向相同或者相近的人的建议。这就是UserCF在现实中的实例，所以说该算法会推荐跟你兴趣爱好相似的人的喜欢的物品。（哈哈，描述的有点绕）

这里还想再啰嗦几句，UserCF其实就是一个给用户聚类的过程，把用户按照兴趣口味聚类成不同的群体，给用户的推荐就来自于这个群体。所以要做好这个推荐关键就在于如何量化”口味相似“这个看起来很简单直接的事情，这关系到用户对推荐系统体验好坏的问题。

从上面的例子来说，基于用户的协同过滤算法主要包括了两个步骤：

1. 找到和目标用户兴趣相似的用户合集
2. 找到这个集合中的用户喜欢的，且目标用户没有见过的物品推荐给目标用户

第一步的关键就是计算两个用户的兴趣相似度。在前面提到过那个非常重要的关系矩阵（Matrix），这里终于要派上用场啦，是不是很期待…言归正传，我们需要先准备用户向量，然后两两计算用户向量的相似度。同时，我们需要设定一个相似度阈值或者一个最大数量，为每个用户保留与其最相似的用户。至于计算相似度的方法在下文中介绍。

1.得到用户向量的前提是用户在我们的产品中有行为数据
2. 用户向量的维度就是物品的个数
3. 用户向量是稀疏的，也就是说并不是每个维度都有数值

第二步：在经过第一步的计算之后，我们就得到了一个和目标用户兴趣相似的用户合集，接下来就是用户最爱的推荐环节…把和他”臭味相投“的用户喜欢的物品汇总起来，去掉用户已经消费过物品，剩下的排序就是推荐结果。这里说一下汇总的方式，我们用一个公式来表示：

$$P_{u,i}=\frac{{\sum }_j^n(si{m}_{u,j}\ast R_{j,i})}{{\sum }_j^{n}si{m}_{u,j}}$$

公式说明：$u$表示用户$u$，$i$表示物品$i$，$j$表示用户$j$，$n$表示总用户数，$si{m}_{u,j}$表示用户$u$和$j$的相似度，$R_{j,i}$表示用户$j$对物品$i$的评分，$P_{u,i}$表示预估用户$u$对物品$i$的评分。

公式解读： 这个公式等号的左边是计算一个物品$i$和一个用户$u$的匹配分数，等号右边是这个分数的计算过程。分母是把和用户$u$相似的$n$个用户的相似度累加起来，分子是把这$n$个用户各自对物品$i$的态度按照相似度加权求和，这里的态度最简单的就是”0“和”1“，”1“表示喜欢，”0“表示不喜欢，如果是评分的话，则可以是0~5之间的取值。整个公式的结果就是相似用户的态度加权平均值。

最后，想说的是基于用户的协同过滤算法有以下两个产出：

• 相似用户列表 基于用户的推荐结果
• 基于物品的相似度计算（ItemCF）

所以我们不但可以推荐物品，还可以推荐用户！比如在一个社交平台上看到的”相似粉丝”和你“和你口味相似的人”等等。

基于用户的协同过滤算法（UserCF）有其弊端：

• 在互联网应用场景下，用户数量往往远大于物品数量，这就导致维护和存储这些相似度矩阵的开销非常大

• 用户的历史数据向量往往非常稀疏，，对只有几次购买或者点击的用户来说，找到相似的用户准确度是非常的低的

• 用户的兴趣爱好是会变化的，不是静态的，所以兴趣改变问题很难被反映出来

  ---

2. 基于物品的协同过滤算法（ItemCF）

由于UserCF存在上述三点缺陷，所以在业界更多还是采用ItemCF，比如Amazon、Netflix、Hulu等等。

ItemCF是通过计算用户关系矩阵中物品列向量的相似度得到物品之间的相似矩阵，再找到用户的历史正反馈物品的相似物品进行进一步排序和推荐，ItemCF的具体步骤如下：

1. 基于用户历史数据，构建如图1所示的用户关系矩阵
2. 计算用户关系矩阵两两列向量间的相似性（计算方式与用户相似度计算方式相同），构建$n\ast n$维的物品相似度矩阵
3. 获得用户历史行为数据中的正反馈物品列表
4. 利用物品相似度矩阵，针对目标用户历史行为中的正反馈物品，找出相似的Top k个物品，组成相似物品集合
5. 对相似物品集合中的物品，利用相似度分值进行排序，生成最终的推荐列表

在第5步中，如果一个物品与多个用户行为历史中的正反馈物品相似，那么该物品最终的相似度应该是多个相似度的累加，如下式所示：

$$R_{u,p}=\sum _{h\in H}(W_{p,h}\ast R_{u,h})$$

其中，$H$是目标用户的正反馈物品集合，$W_{p,h}$是物品$p$与物品$h$的物品相似度，$R_{u,h}$是用户$u$对物品$h$的已有评分。

在得到物品的相似度之后，接下来就是为用户推荐他可能感兴趣的物品，基于物品的协同过滤算法有两种应用场景：

1. 第一种是Top $k$推荐，尝尝表现为类似“猜你喜欢”这样的形式。触发方式是当用户访问首页时，汇总和用户已经消费过的物品相似的物品，按照汇总后分数从高到低推出。汇总的公式是这样的：

$$\widehat{R_{ui}}=\frac{{\sum }_{j=1}^{m}sim(i,j)\times R_{uj}}{{\sum }_{j=1}^{m}sim(i,j)}$$

要预测一个用户$u$对一个物品$i$的评分数，就要遍历用户$u$评分过的所有物品。假如一共有$m$个物品，用每一个物品和待计算物品$i$的相似度乘以用户的评分，加权求和后除以所有这些相似度的总和，就得到了一个加权平均评分，作为用户$u$对物品$i$的分数预测。

2. 第二种属于相关推荐，也就是本节开篇时提到的场景。当用户访问一个物品的详情页面时，后者完成一个物品消费的结果页面时，可以直接获取这个物品的相似物品推荐，也就是“看了又看”或者“买了又买”。

之前的UserCF算法有改良版的算法，这里对于ItemCF也有对应改良版的——Slope One算法，这里先留个坑，以后再说吧。。。键盘敲得的手很累，先偷个懒，哈哈哈。。。

3. 相似度计算方法

在协同过滤算法中，用户相似度的计算是算法中最关键的一步。在图1中，关系矩阵的行向量代表相应用户的用户向量。那么计算用户$i$和用户$j$的相似度问题，就是计算用户向量$i$和用户向量$j$之间的相似度问题了。好了，言归正传，常用的两个向量的相似度计算方法有以下几种：

1. 余弦相似度

余弦相似度衡量了用户$i$和$j$向量之间的向量夹角大小。显然，向量夹角越小，证明余弦相似度越大，两个用户越相似。余弦相似度公式：

$$sim(i,j)=cos(i,j)=\frac{i\ast j}{||i||\ast ||j||}$$

$||i||$是对向量$i$中每个元素平方求和再开方。

余弦相似度对绝对值大小不敏感，所以在某些情况下是有问题的。例如：用户A对两部电影的评分分别为1分和2分，用户B对两部电影的评分分别为4分和5分，通过计算余弦相似度，两个用户相似度达到0.98，这显然是不合理的。

针对上面说的这个问题，对余弦相似度进行改进，改进后的叫做调整的余弦相似度。调整的方法很简单，就是先计算向量每个维度上的均值，然后每个向量在各个维度上都减去均值后再计算余弦相似度。前面的小例子，如果使用调整后的余弦相似度计算得到的相似度分数为-0.1，即表示两个用户的口味相反。

2. 皮尔逊相关系数

相比余弦相似度，皮尔逊相关系数通过使用用户平均分对各独立评分进行修正，减小了用户评分偏置影响。

$$sim(i,j)=\frac{{\sum }_{p\in P}(R_{i,p}-R_i)(R_{j,p}-R_j)}{\sqrt{{\sum }_{p\in P}(R_{i,p}-R_i{)}^2}\ast \sqrt{{\sum }_{p\in P}(R_{j,p}-R_j{)}^2}}$$

其中，$R_{i,p}$代表用户$i$对物品$p$的评分。$R_i$代表用户$i$对所有物品的平均评分，$P$代表所有物品的集合。

3. 改进的皮尔逊相关系数思路：通过引入物品平均分的方式，减少物品评分偏置对结果的影响。

$$sim(i,j)=\frac{{\sum }_{p\in P}(R_{i,p}-R_p)(R_{j,p}-R_p)}{\sqrt{{\sum }_{p\in P}(R_{i,p}-R_p{)}^2}\ast \sqrt{{\sum }_{p\in P}(R_{j,p}-R_p{)}^2}}$$

其中，$R_p$代表物品$p$得到所有评分的平均分。

4. 欧氏距离

顾名思义，欧氏距离就是一个欧式空间下度量距离的方法。两个点$p$和$q$在同一欧式空间下之间的距离计算方式为：

$$E(p,q)=\sqrt{\sum _{i=1}^n(p_i-q_i{)}^2}$$

公式中的$n$是空间维度，也可以理解为坐标轴的个数，$p_i$和$q_i$就是每一个坐标上的取值。显示，欧氏距离不适合布尔向量之间使用。

欧式距离的值是一个非负数，最大值是正无穷。所以当我们期望的值得范围是[0,1]或者[-1,1]之间的话，我们需要经过二次转换，转换公式为：

$$\frac{1}{1+E(p,q)}$$

欧式距离测量的是空间中两个点的绝对差异，适用于分析用户能力模型之间的差异，比如消费能力、贡献内容能力等。它的计算结果是一个绝对的客观值，而不是相对值，差异是多大就是多大。

5. Jaccard相似度

Jaccard相似度表示两个集合的交集元素个数占并集元素个数的比例。Jaccard相似度非常适用于布尔向量。假设$P$和$Q$是两个集合，两集合元素去重后有$n$个，把两个集合表示为布尔向量$p$和$q$，如果第$i$个元素出现在集合$P$中，那么$p_i=1$，否则$p_i=0$。计算两个向量的Jaccard相似度的方式如下：

$$J(p,q)=\frac{|P\bigcap Q|}{|P\bigcup Q|}=\frac{{\sum }_{i=0}^n{p}_i{q}_i}{{\sum }_{i=0}^n{p}_i|q_i}$$

• 上式中分子为两个布尔向量做点积计算，得到的是交集元素的个数
• 分母为两个布尔向量做或运算，再求元素和，即并集元素个数

余弦相似度适用于评分数据，Jaccard相似度适用于隐式反馈数据。例如用户的收藏行为计算用户之间的相似度就适合使用Jaccard相似度。

最后想说的是，在相似用户的计算过程中，理论上，任何合理的”向量相似度定义方式“都可以作为相似用户计算的标准。

4. 协同过滤算法的进化—矩阵分解

1. 概述。

上面谈到了基于近邻模型的召回算法，这中算法是存在弊端的：

• 物品之间存在相关性，信息量并不随着向量维度的增加而线性增加
• 矩阵元素稀疏，计算结果不稳定。增减一个向量维度，可能会导致近邻结果差异很大

上面两个问题都可以在矩阵分解中得以解决。直观上说，矩阵分解就是把原来的大矩阵，近似分解成两个小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。

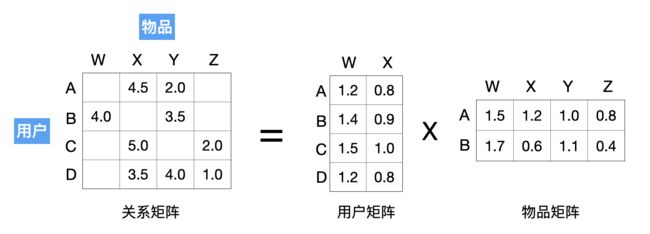
矩阵分解算法将$m$ x $n$维的关系矩阵$R$分解为$m$x$k$维的用户矩阵$U$和$k$x$n$维的物品矩阵$V$相乘的形式。其中$m$是用户数量，$n$是物品数量，$k$是隐向量的维度。$k$的大小决定了隐向量表达能力的强弱。$k$的取值越小，隐向量包含的信息就越少，模型的泛化程度越高；反之，$k$取值越大，隐向量的表达能力越强，但泛化程度相应降低。此外，$k$的取值还与矩阵分解的求解复杂度直接相关。在具体应用中，$k$的取值要经过多次试验找到一个推荐效果和工程开销的平衡点。

基于用户矩阵$U$和物品矩阵$V$，用户$u$对物品$i$的预估评分如下面公式所示：
$$\widehat{r_{ui}}=q_i^T{p}_u$$

其中$p_u$是用户$u$在用户矩阵$U$中对应行向量，$q_i$是物品$i$在物品矩阵$V$中对应的列向量。

---

2. 矩阵分解的求解过程

对矩阵进行矩阵分解主要方法就是利用梯度下降法进行求解。既然涉及到了梯度下降法，就必不可少的需要相应的目标函数（如下式所示），该目标函数的目的是让原始评分$r_{u,i}$与用户向量和物品向量之积 ${{\mathbf{q}}_{\mathbf{i}}}^{\mathrm{T}}{p}_u$ 的差尽量小，这样才能最大限度的保存用户关系矩阵中的原始信息。

$$\underset{q^{\ast },p^{\ast }}{\min }\sum _{(u,i)\in K}(r_{ui}-q_i^T{p}_u{)}^2$$

其中$K$是所有用户评分样本的集合。为了减小过拟合现象，加入正则化后的目标函数如下式所示：
$$\underset{q^{\ast },p^{\ast }}{\min }\sum _{(u,i)\in K}(r_{ui}-q_i^T{p}_u{)}^2+\lambda (||q_i||+||p_u||{)}^2$$

整个梯度下降法标准求解过程：

1. 准备好用户关系矩阵$R$，将$R$中的每一条频分数据看做一条训练样本；
2. 给分解后的$P$矩阵和$Q$矩阵随机初始化元素值；
3. 确定目标函数（上式），用来计算$P$矩阵和$Q$矩阵的预测值与真实值之间的差异；
4. 对目标函数求偏导，取梯度下降的方向和幅度；
5. 利用第4步的求导结果，沿梯度的反方向更新参数和$P$矩阵和$Q$矩阵中的元素值；
6. 当迭代次数超过上限$n$或损失低于阈值$\theta$时，结束训练否则循环第3步。

在完成矩阵分解过程后，即可得到所有用户和物品的隐向量。在对某用户进行推荐时，可利用还用户的隐向量与所有物品的隐向量进行逐一内积运算，得出该用户对所有物品的频分预测，再逐次排序，得到最终的推荐列表。之所以说矩阵分解相对基于近邻的协同有更强的泛化能力，主要是因为矩阵分解过程中产生的隐向量，隐向量生成的过程其实就是对用户物品关系矩阵的全局拟合的过程，因此隐向量是利用全局信息生成的。

---

3. 谈谈矩阵分解的优缺点

相比基于近邻的协同过滤算法来说，MF有以下几个优点：

• 泛化能力强。一定程度上解决了数据稀疏的问题 ；
• 空间复杂度低 。只需存储用户和物品的隐向量，空间复杂度由$n^2$级别降到$(n+m)\ast k$级别；
• 更好的扩展性与灵活性

其局限性：

• 缺乏用户历史行为时，无法进行有效的推荐；
• MF不方便加入用户、物品和上下文相关的特征。

---

参考文章：

1. 《推荐系统》陈开江著
2. 《推荐系统实践》项亮著
3. 《深度学习推荐系统》王喆著
4. 《美团机器学习实践》美团算法团队著
5. https://zhuanlan.zhihu.com/p/58198384
6. https://blog.csdn.net/nicajonh/article/details/79657317