(02)Cartographer源码无死角解析-(38) PoseExtrapolator→AdvanceImuTracker()、ImuTracker姿态推断

讲解关于slam一系列文章汇总链接:史上最全slam从零开始，针对于本栏目讲解(02)Cartographer源码无死角解析-链接如下:
(02)Cartographer源码无死角解析- (00)目录_最新无死角讲解：https://blog.csdn.net/weixin_43013761/article/details/127350885
 
$文末正下方中心提供了本人联系方式，点击本人照片即可显示WX\to 官方认证$
 

一、前言

在上一篇博客中，对 src/cartographer/cartographer/mapping/pose_extrapolator.cc 文件中的 PoseExtrapolator::AddPose() 进行了讲解，其中有两个重要的函数：

  // 根据加入的pose计算线速度与角速度
  UpdateVelocitiesFromPoses();

  // 将imu_tracker_更新到time时刻
  AdvanceImuTracker(time, imu_tracker_.get());

前者 UpdateVelocitiesFromPoses() 会根据剪裁过的 timed_pose_queue_ 队列数据，计算线速度与角速度，分别存储在成员变量 linear_velocity_from_poses_ 与 angular_velocity_from_poses_ 之中。对于后者 AdvanceImuTracker() 函数暂未分析，另外在 PoseExtrapolator::AddPose() 函数中，还创建了好些 ImuTracker 对象指针：

    imu_tracker_ = absl::make_unique<ImuTracker>(gravity_time_constant_, tracker_start);
    odometry_imu_tracker_ = absl::make_unique<ImuTracker>(*imu_tracker_);
    extrapolation_imu_tracker_ = absl::make_unique<ImuTracker>(*imu_tracker_);

很明显，接下来的内容与 ImuTracker 这个类是息息相关的了，前面一直在逃避，闲现在肯定躲避不了了，不过没有关系，对齐进行详细分析即可。该类也比较简单，实现于 src/cartographer/cartographer/mapping/imu_tracker.cc 文件中。

$顺着该思路阅读源码：$ ImuTracker 这个类主要的作用，是可以输入一个时间 time，然后预测出该时间点的姿态 orientation_。其预测的原理，是利用上一时刻 Imu 的角速度。另外还会利用 Imu 的线性加速度对最新的 orientation_ 进行校正。
 

二、构造函数

在 ImuTracker 中定义了如下成员变量：

 private:
  const double imu_gravity_time_constant_; //Imu 重力时间参量，
  common::Time time_; //时间点
  common::Time last_linear_acceleration_time_; //最后(最近)线性加速度的时间点
  Eigen::Quaterniond orientation_; //四元数表示的旋转
  Eigen::Vector3d gravity_vector_; //重力方向向量
  Eigen::Vector3d imu_angular_velocity_; //Imu角速度

如果不是很明白其含义，也没有关系，先来看一下 ImuTracker 的构造函数：

/**
 * @brief Construct a new Imu Tracker:: Imu Tracker object
 * 
 * @param[in] imu_gravity_time_constant 这个值在2d与3d情况下都为10
 * @param[in] time 
 */
ImuTracker::ImuTracker(const double imu_gravity_time_constant,
                       const common::Time time)
    : imu_gravity_time_constant_(imu_gravity_time_constant),
      time_(time),
      last_linear_acceleration_time_(common::Time::min()),
      orientation_(Eigen::Quaterniond::Identity()), // 初始方向角
      gravity_vector_(Eigen::Vector3d::UnitZ()),    // 重力方向初始化为[0,0,1]
      imu_angular_velocity_(Eigen::Vector3d::Zero()) {}

首先传入一个重力时间常量，通过初始化列表赋值给 imu_gravity_time_constant_，时间点 time_ 也一样。稍后再来看该时间点具体是什么的时间点。初始化 last_linear_acceleration_time_ 为最小时间点。orientation_ 初始化为实部为1，虚部为0的四元数，可以理解为单位旋转矩阵。

$gravity\_vector\_$ 是一个比较重要的变量，初始化的 gravity_vector_ 是一个单位向量 (0,0,1)。显然，初始时 orientation_ 与 gravity_vector_ 乘积也为(0,0,1)。另外需要知道，世界坐标系中，Z轴是与重力方向平行的。

最后剩下的 imu_angular_velocity_变量初始化成全为0的向量。ImuTracker 中的有三个成员函数：

void ImuTracker::Advance(const common::Time time) {CHECK_LE(time_, time);
void ImuTracker::AddImuLinearAccelerationObservation(const Eigen::Vector3d& imu_linear_acceleration)
void ImuTracker::AddImuAngularVelocityObservation(const Eigen::Vector3d& imu_angular_velocity)

其并没有相互调用关系，那么就按顺序来，一个一个对其进行分析吧。
 

三、ImuTracker::Advance()

该成员函数，需要传入一个时间参数 const common::Time time。代码注释如下：

/**
 * @brief 预测出time时刻的姿态与重力方向
 * 
 * @param[in] time 要预测的时刻
 */
void ImuTracker::Advance(const common::Time time) {
  CHECK_LE(time_, time);
  const double delta_t = common::ToSeconds(time - time_);
  // 上一时刻的角速度乘以时间,得到当前时刻相对于上一时刻的预测的姿态变化量,再转换成四元数
  const Eigen::Quaterniond rotation =
      transform::AngleAxisVectorToRotationQuaternion(
          Eigen::Vector3d(imu_angular_velocity_ * delta_t));
  // 使用上一时刻的姿态 orientation_ 乘以姿态变化量, 得到当前时刻的预测出的姿态
  orientation_ = (orientation_ * rotation).normalized();

  // 根据预测出的姿态变化量,预测旋转后的线性加速度的值
  gravity_vector_ = rotation.conjugate() * gravity_vector_;
  // 更新时间
  time_ = time;
}

$(1)$ 传入的时间参数 time 其会计算与 time_ 的差值，获得时间段 delta_t。然后调用了 transform::AngleAxisVectorToRotationQuaternion() 函数，该函数的作用与前面介绍的 transform::RotationQuaternionToAngleAxisVector() 函数用作刚好相反，可以把一个轴角(旋转向量转换成一个四元数)

可以参考 史上最简SLAM零基础解读(8.1) - 旋转矩阵、旋转向量、欧拉角推导与相互转换，其中有相关公式的推导过程。这里是通过角速度乘以时间段求轴角(旋转向量)的，具体公式推导再上一篇博客已经进行过推导，这里就不在重复了。

$(2)$ 通过步骤(1) 求解出来的时上一时刻到 time_ 到 time 时刻(当前)的姿态变换rotation，这里
        ①记 time_ 时刻的姿态 orientation_ 记为 $orientatio{n}_{time\_}^{init}$，其中 init 表示初始姿态。
        ②记 time 时刻的姿态，为 $orientatio{n}_{time}^{init}$其中 init 表示初始姿态。
        ③记 rotation，为 $rotatio{n}_{time}^{time\_}$，表示 time_ 时刻到 time 时刻的之态变化。
显然成立如下公式：
$$orientatio{n}_{time}^{init}=orientatio{n}_{time\_}^{init}\ast rotatio{n}_{time}^{time\_}\text{\hspace{1em}(01)}$$，
$(3)$ rotation表示绕旋转轴逆时针旋转一定角度，那么 rotation.conjugate() 表示绕旋转轴顺时针旋转一定角度。可知：

gravity_vector_ = rotation.conjugate() * gravity_vector_;

表示 gravity_vector_ 绕 rotation 的旋转轴顺时针旋转一定角度，其与步骤(2)是相反的。rotation 是一个位姿变换，该变换的共轭作用作用在 gravity_vector_ 之后，再重新赋值给 gravity_vector_。
        ①rotation与前面保持一致，记为 $rotatio{n}_{time}^{time\_}$，
        ②gravity_vector_ 表示相对于初始状态的线性加速度
        ③记$gravity\_vecto{r}_{time\_}^{init}$，表示相对于初始状态的 time_ 时刻的线性加速度。
        ④记$gravity\_vecto{r}_{time}^{init}$，表示相对于初始状态的 time 时刻的线性加速度。
        ⑤$记gravity\_vecto{r}_{time}^{time\_}$，表示相对于time_ 时刻下 time 时刻的线性加速度。

构造函数中 gravity_vector_ 初始状态为(0,0,1),记为，根据上面几号，可以推导出如下数学公式：
$$gravity\_vecto{r}_{time\_}^{time}=[rotatio{n}_{time}^{time\_}{]}^{-1}\ast gravity\_vecto{r}_{time\_}^{init}\text{\hspace{1em}(02)}$$该公式看起来貌似不知道做啥，把 gravity_vector 绕 了 rotation 反方向旋转一定角度？因为四元数的共轭表示绕旋转轴反向旋转(顺时针)。

 
$总结：$有的朋友可能比较迷糊，为什么步骤(2)与步骤(3)，也就是对 orientation_ 与 gravity_vector_的更新是相反的。这里是埋了一个伏笔，注意到
        $\to orientation\_初始化时，实部为1，虚部为0。$
        $\to gravity\_vector\_初始化时，为(0,0,1)单位向量$

如果把 $orientatio{n}_{time}^{init}$ 与 $gravity\_vecto{r}_{time\_}^{time}$ 乘起来可以得到如下结果：
$$\{orientatio{n}_{time\_}^{init}\ast rotatio{n}_{time}^{time\_}\}\ast \{[rotatio{n}_{time}^{time\_}{]}^{-1}\ast gravity\_vecto{r}_{time\_}^{init}\}\text{\hspace{1em}(03)}$$上式等价于$$orientatio{n}_{time\_}^{init}\ast gravity\_vecto{r}_{time\_}^{init}=(1,0,0,0)\ast (0,0,1)=(0,0,1)\text{\hspace{1em}(04)}$$ 也就是说，ImuTracker 在不停更新 orientation_ 与 gravity_vector_ 过程中，他们的乘以应一直保持单位向量(0,0,1)。

 

四、ImuTracker::AddImuLinearAccelerationObservation()→代码流程

该函数稍微复杂一点，不过没有关系：

$(1)$ 调用该函数，需要传入一个三维的 Imu 线性加速度 imu_linear_acceleration，这里很有可能就是传入 Imu 测量到的数据，也可以理解为每个时刻 Imu 的位姿，注意这里的是加速度，不是角速度，也不是角加速度。
 
$(2)$ 在前面 ImuTracker::Advance() 函数中，会对变量 time_ 进行更新。因为构造函数初始化 last_linear_acceleration_time_ 变量是就是 common::Time::min()，如果 last_linear_acceleration_time_ > common::Time::min() 成立，说明 last_linear_acceleration_time_ 被更新过了，那么技计算 time_ 与 last_linear_acceleration_time_ 的差值给 delta_t，否则返回一个 double 类型的最大值给 delta_t。同时把 time_ 赋值给 last_linear_acceleration_time_。
 
$(3)$ 求权重 alpha，其与 delta_t 相关，公式为 $$alpha=1-{\exp }^{(-delta\_t/10)}⟹\alpha =1-exp(-\delta t/10)$$从公式可以看出，delta_t 越大，alpha 越大，但是 alpha最大 为1，代码如下：

  // Step: 2 求alpha, alpha=1-e^(-delta_t/10)
  // delta_t越大, alpha越大
  const double alpha = 1. - std::exp(-delta_t / imu_gravity_time_constant_);

也就是说，单第一次 last_linear_acceleration_time_ 没有被更新过，alpha 接近1。alpha 还与 imu_gravity_time_constant_ 参数相关。本人利用软件绘画了一下该函数的图示(https://www.desmos.com/calculator?lang=zh-CN)：

 
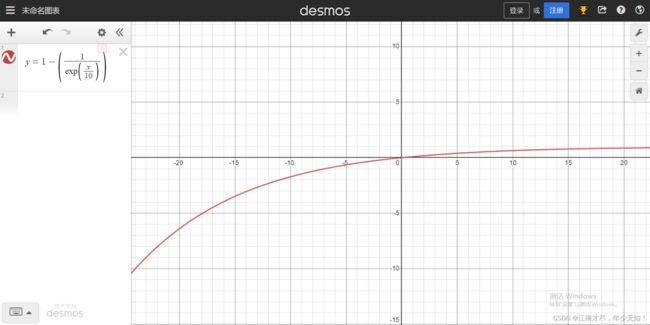
$(4)$ 使用 alpha 来确定权重，代码如下：

  // 指数来确定权重, 因为有噪声的存在, 时间差越大, 当前的线性加速度的权重越大
  // 这里的gravity_vector_改成线性加速度更清晰一些
  gravity_vector_ =
      (1. - alpha) * gravity_vector_ + alpha * imu_linear_acceleration;

结合(3)总的来说，当时间差 delta_t 比较下，则相信历史记录的 gravity_vector_，如果 delta_t 比较大，则相信新传入的 Imu 位姿 imu_linear_acceleration。总的来说，这里通过外部传入，或者说观测到 imu_linear_acceleration 数据，对 gravity_vector_ 进行更新(由上一次更新到当前)，从这里可以看出来，gravity_vector_ 与 imu_linear_acceleration 联系十分紧密。
 
$(5)$ 对 gravity_vector_ 更新之后，就是要对 orientation_ 进行更新了，前面提到过他们的乘积永远需要保持在 (0,0,1) 左右。要对 orientation_ 进行更新，那么肯定需要算出当前的 gravity_vector_ 与 上一次的 gravity_vector_ 的旋转变换量。上一次机器人的位姿为 orientation_ 记为 $orientatio{n}_{time\_}^{init}$，使用他的逆乘初始值(0,0,1)向量，那么可以得到 gravity_vector_ 上一时刻的加速度，代码如下

orientation_.conjugate() * Eigen::Vector3d::UnitZ()  //就表示 gravity_vector_ 上一次的位姿。

 
$(6)$ 接着调用了 Eigen 中的 Quaternion::FromTwoVectors 函数，后续为大家讲解一下其推导过程，这里先略过。该函数主要的功能就是求两个3维向量之间的旋转，这个旋转以四元数的方式返回。就是说：

  // Change the 'orientation_' so that it agrees with the current
  // 'gravity_vector_'.
  // Step: 4 求得 线性加速度的值 与 由上一时刻姿态求出的线性加速度 间的旋转量
  const Eigen::Quaterniond rotation = FromTwoVectors(
      gravity_vector_, orientation_.conjugate() * Eigen::Vector3d::UnitZ());

求解的就是当前次 gravity_vector_ 到上一次 gravity_vector_ 的角速度变换量(四元数表示)。

$(7)$ 步骤(6)求解出来的 rotation 是 gravity_vector_ 到上一次 gravity_vector_ 的旋转，那么其为正方向(逆时针)的旋转变化，orientation_ 与其相乘，然后再赋值给 orientation_，相当于对 orientation_。进行了更新。

$(8)$ 通过如下函数，对 orientation_ 与 gravity_vector_ 进行校验：

  // note: glog CHECK_GT: 第一个参数要大于第二个参数
  // 如果线性加速度与姿态均计算完全正确,那这二者的乘积应该是 0 0 1
  CHECK_GT((orientation_ * gravity_vector_).z(), 0.);
  CHECK_GT((orientation_ * gravity_vector_).normalized().z(), 0.99);

 

四、ImuTracker::AddImuLinearAccelerationObservation()→代码注释

关于 ImuTracker::AddImuLinearAccelerationObservation() 函数的注释如下：

/**
 * @brief 更新线性加速度的值,并根据重力的方向对上一时刻的姿态进行校准
 * 
 * @param[in] imu_linear_acceleration imu的线加速度的大小
 */
void ImuTracker::AddImuLinearAccelerationObservation(
    const Eigen::Vector3d& imu_linear_acceleration) {
  // Update the 'gravity_vector_' with an exponential moving average using the
  // 'imu_gravity_time_constant'.
  // 指数滑动平均法 exponential moving average
 
  // Step: 1 求delta_t, delta_t初始时刻为infinity, 之后为time_-last_linear_acceleration_time_
  const double delta_t =
      last_linear_acceleration_time_ > common::Time::min()
          ? common::ToSeconds(time_ - last_linear_acceleration_time_)
          : std::numeric_limits<double>::infinity();
  last_linear_acceleration_time_ = time_;

  // Step: 2 求alpha, alpha=1-e^(-delta_t/10)
  // delta_t越大, alpha越大
  const double alpha = 1. - std::exp(-delta_t / imu_gravity_time_constant_);

  // Step: 3 将之前的线加速度与当前传入的线加速度进行融合, 这里采用指数滑动平均法

  // 指数来确定权重, 因为有噪声的存在, 时间差越大, 当前的线性加速度的权重越大
  // 这里的gravity_vector_改成线性加速度更清晰一些
  gravity_vector_ =
      (1. - alpha) * gravity_vector_ + alpha * imu_linear_acceleration;
      
  // Change the 'orientation_' so that it agrees with the current
  // 'gravity_vector_'.
  // Step: 4 求得 线性加速度的值 与 由上一时刻姿态求出的线性加速度 间的旋转量
  const Eigen::Quaterniond rotation = FromTwoVectors(
      gravity_vector_, orientation_.conjugate() * Eigen::Vector3d::UnitZ());

  // Step: 5 使用这个旋转量来校准当前的姿态
  orientation_ = (orientation_ * rotation).normalized();

  // note: glog CHECK_GT: 第一个参数要大于第二个参数
  // 如果线性加速度与姿态均计算完全正确,那这二者的乘积应该是 0 0 1
  CHECK_GT((orientation_ * gravity_vector_).z(), 0.);
  CHECK_GT((orientation_ * gravity_vector_).normalized().z(), 0.99);
}

 

五、ImuTracker::AddImuAngularVelocityObservation

该函数比较简单，添加Imu测量到的加速度：

// 更新角速度
void ImuTracker::AddImuAngularVelocityObservation(
    const Eigen::Vector3d& imu_angular_velocity) {
  imu_angular_velocity_ = imu_angular_velocity;
}

 

六、ImuTracker 总体复盘

通过上面的分析，下面来做一个总结：

$(1)$ 总体来说， ImuTracker 的作用应该是根据之前的 Imu 数据推断出指定 time 时刻位姿(可以早于当前时刻)，调用 ImuTracker::orientation() 函数查询。构造函数：orientation_ 初始化为→实部为1，虚部为0；gravity_vector_ 初始化为→(0,0,1)单位向量；

$(2)$ 预测时先调用 ImuTracker::Advance(const common::Time time) 函数，该函数会利用存储的最新角速度 imu_angular_velocity_ 对 orientation_ 与 gravity_vector_ 进行更新。注意 orientation_ 逆时针更新，gravity_vector_ 顺时针更新。更新之后，所以把 time_ 刷新，赋值成 time。可以知道，该函数更新只使用到了最新的角速度 imu_angular_velocity_ 。

$(3)$ 那么最新的角速度从哪里来，Imu的线性加速度又有什么作用？其 ImuTracker 内部又是如何工作的呢？想要 ImuTracker 正常的工作起来，需要不停的调用如下函数：

//添加观测到的，或者说通过Imu测量到的线性加速度。
void ImuTracker::AddImuLinearAccelerationObservation(const Eigen::Vector3d&imu_linear_acceleration) 
//添加观测到的。或者说通过Imu测量到的角速度。
void ImuTracker::AddImuAngularVelocityObservation(const Eigen::Vector3d& imu_angular_velocity)

$(4)$ AddImuLinearAccelerationObservation()：该函时数添Imu测量的线性加速度，本质上是利用线性加速度对 gravity_vector_ 与 orientation_ 进行校准。$核心理解$→ImuTracker::Advance 函数进行位姿推断的时候，会对 orientation_、gravity_vector_ 进行更新，长时间不进行校准，或导致 orientation_、gravity_vector_ 发生漂移。

$(5)$ AddImuLinearAccelerationObservation()：该函数对于 gravity_vector_ 的更新不太好理解，首先就是使用了一个时间指数平滑平均。时间差越大，历史的 gravity_vector_ 权重就越小。举例：长时间没有获取到可用的 Imu 线速度，那么之前的历史 gravity_vector_ 也就没有太大参考价值了。

$(6)$ AddImuLinearAccelerationObservation()：该函数 gravity_vector_ 的更新，实际上就 Imu 传感器获得的线性加速度的更新。该更新没有只依靠变量 imu_linear_acceleration。

$(7)$ AddImuLinearAccelerationObservation()：该函数是利用 imu_linear_acceleration 数据，对 orientation_(姿态进行校准)
 

七、结语

ImuTracker 这个类主要的作用，是可以输入一个时间 time，然后预测出该时间点的姿态 orientation_。其预测的原理，是利用上一时刻 Imu 的角速度。另外还会利用 Imu 的线性加速度对最新的 orientation_ 进行校正。

这里很明显存在一个局限性，那就是校正使用 Imu 的线性加速度，其只有在物体慢速或者匀速的状态下，才能起到较好的作用，且按原理来说，ImuTracker 初始化必须处于静止状态。可以参考一下 Imu 的预积分，其可以解决该问题，也算对 Cartographer 优化的一个方向。参考论文：

论文：D-LIOM: Tightly-coupled Direct LiDAR-Inertial Odometry and Mapping
源码：https://github.com/peterWon/D-LIOM

贡献(Imu方面)：D-LIOM支持与6轴IMU配合的传感器配置初始化，不论机器人载体是静态或运动状态，都可以完成imu的初始化功能并使得估计状态与重力对齐。D-LIOM前端还可以利用imu预积分的功能完成多激光雷达输入和点云去畸变。