数据挖掘第二课

facebook案例

还是原来的案例，经过学习改进之后的分析过程

import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

导入数据

train_facebook = pd.read_csv(r'D:\学习资料\数据挖掘\第二讲数据理解与准备\dataset\train_facebook.csv', encoding = 'gbk')
test_facebook = pd.read_csv(r'D:\学习资料\数据挖掘\第二讲数据理解与准备\dataset\train_facebook待预测.csv', encoding = 'gbk')

1. 数据预处理

      1.1 描述性统计

train = train_facebook[:10000]
test = test_facebook[10000:]
true = train_facebook.loc[10000:, 'y']
train.describe()

     1.2 哑变量生成

## 数据集中有些特征不是数值型的，而是字符型的，无法运算
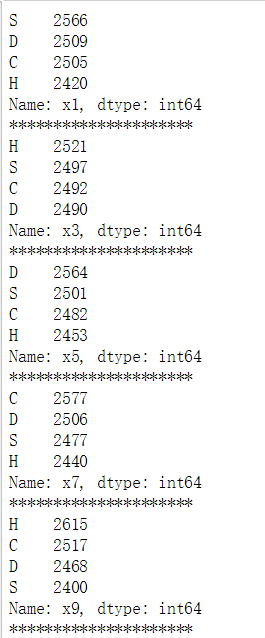
dummies_dat = ['x1', 'x3', 'x5', 'x7', 'x9']
for i in dummies_dat:
    print(train[i].value_counts())
    print('*********************')

trains = train.copy()
for i in dummies_dat:  ## 生产哑变量
    dummies_ = pd.get_dummies(train[i], prefix = i)
    trains = trains.join(dummies_)
trains

## 删去原行，为了避免多次共线性，另删去w为D的行
drop_dat = dummies_dat.copy()
for i in dummies_dat:
    s = i + '_D'
    drop_dat.append(s)
trains.drop(columns = drop_dat, inplace = True)
## 本例中数据无缺失值，而且基本可以认为是离散的数据，因此亦不须离群值探索，直接进行指标选择

2. 数据可视化分析

## 5个四分类特征
plt.rcParams['font.sans-serif']=['SimHei']    # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False    # 用来正常显示负号
fig = plt.figure(figsize = (16, 20))
dummies_values = ['D', 'S', 'C', 'H']
fig.suptitle('5个四分类特征不同取值时，y的取值情况', fontsize = 20)
for i in range(5):  ## 五个指标
    for j in range(4):   ## 四个分类
        ax = fig.add_subplot(5, 4 ,i * 4 + j + 1)
        ax_values = train.loc[train[dummies_dat[i]] == dummies_values[j], 'y']
        label = ax_values.value_counts().index
        rect = ax.bar(label, ax_values.value_counts() / len(ax_values),color = f'#f{i*2}{i}{i}{i}{j}')
        for rec in rect:
            x = rec.get_x()
            height = rec.get_height()
            ax.text(x + 0.1,1.02 * height,'{:.1f}'.format(height * 100), fontsize = 10)                   
        ax.set_title(f'{dummies_dat[i]}取{dummies_values[j]}')

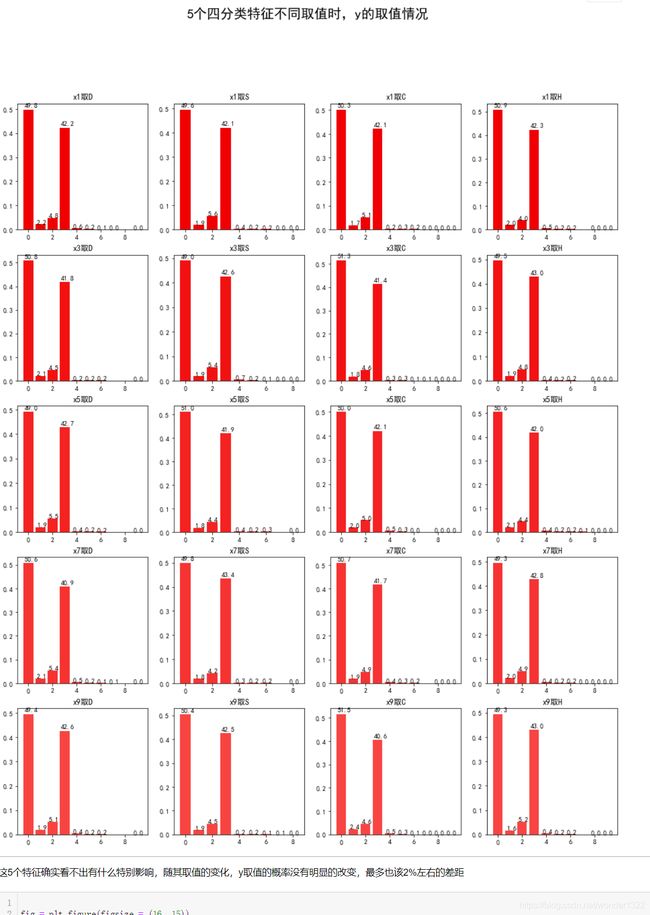
这5个特征确实看不出有什么特别影响，随其取值的变化，y取值的概率没有明显的改变，最多也该2%左右的差距

fig = plt.figure(figsize = (16, 15))
plt.rcParams['font.size'] = 20
for i in range(len(dummies_dat)):
    ax = fig.add_subplot(3, 2, i + 1)
    ax = sns.boxplot(train['y'], train[dummies_dat[i]])

fig = plt.figure(figsize = (16, 15))
plt.rcParams['font.size'] = 20
continuous = ['x2', 'x4', 'x6', 'x8', 'x10']
for i in range(len(continuous)):
    ax = fig.add_subplot(3, 2, i + 1)
    ax = sns.boxplot(train[continuous[i]], train['y'] )

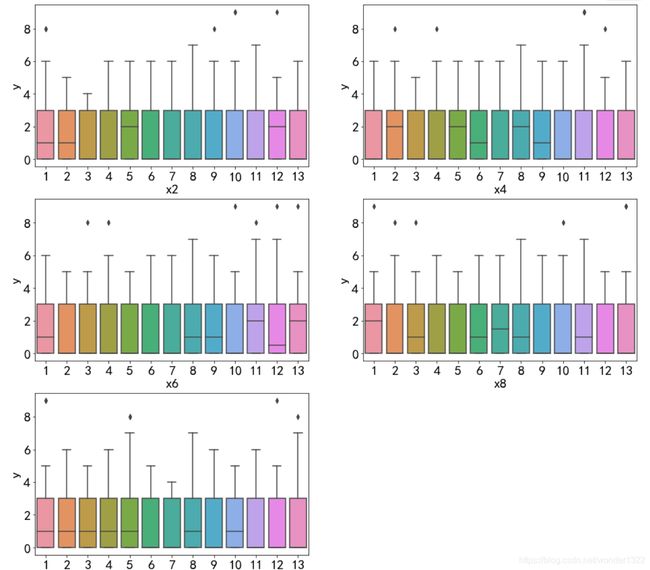
从箱线图看，这10个变量也对y的影响不明显，需使用定性指标来衡量

3.特征选择

     3.1 相关系数

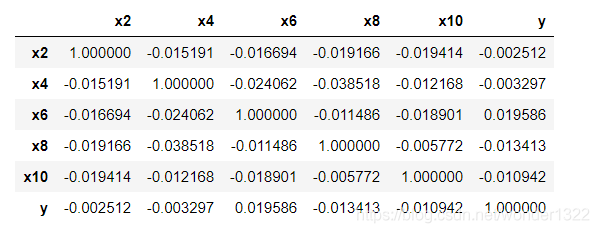
#对于 ['x2', 'x4', 'x6', 'x8', 'x10']可以试试相关系数，但其他几个变量相关系数就不再适用
## pearson 相关系数
train[continuous + ['y']].corr()

## spearman 相关系数
train[continuous + ['y']].corr('spearman')

## Kendall Tau相关系数
train[continuous + ['y']].corr('kendall')

都非常小，没有一个与y的相关系数大于0.1的

    3.2 熵（基尼系数）的指标

def entropy(dat):
    '''
    该函数用于计算熵，主要注意不能有缺失值
    Args:
        dat:要计算的熵的序列            
    Return:
        返回熵的结果
    '''
    prob = dat.value_counts() / len(dat)
    entropys = -sum(np.log2(prob) * prob)
    return entropys
def gini(dat):
    '''
    该函数用于计数基尼系数，主要注意不能有缺失值
     Args:
        dat:要计算的基尼系数的序列            
    Return:
        返回基尼系数的结果
    '''
    prob = dat.value_counts() / len(dat)
    gini = 1 - sum(prob * prob)
    return gini
def gain(date, condition, ways = 'entropy', y = -1):
    '''
    该函数用于计算信息增益，注意不要有缺失值
    Args:
        date: 传入的数据框
        condition: 条件,条件列的名称
        wars:计算信息增益的方法，默认为熵，可选'gini':基尼系数
        y: 目标列的位置，默认为最后一列
    Return:
        返回计算的信息增益
    
    '''
    condition_list = date[condition]
    total_length = len(condition_list)
    indexs = condition_list.value_counts().index
    info_s = 0
    if ways =='entropy':
        info_m = entropy(date.iloc[:, y])
        for i in indexs:
            _aim = date.iloc[(date[condition] == i).values, y]
            info_s += entropy(_aim) * len(_aim)/ total_length    
    elif ways =='gini':
        info_m = gini(date.iloc[:, y])
        for i in indexs:
            _aim = date.iloc[(date[condition] == i).values, y]            
            info_s += gini(_aim) * len(_aim)/ total_length 
    else:
        print('无该方法') 
    gains = info_m - info_s
    return gains

def gain_ratio(date, condition, ways = 'entropy', y = -1):
    '''
    该函数用于计算信息增益率，注意不要有缺失值
    Args:
        date: 传入的数据框
        condition: 条件,条件列的名称
        wars:计算信息增益的方法，默认为熵，可选'gini':基尼系数
        y: 目标列的位置，默认为最后一列
    Return:
        返回计算的信息增益率
    
    '''
    condition_list = date[condition]
    total_length = len(condition_list)
    indexs = condition_list.value_counts().index
    info_s = 0
    if ways =='entropy':
        info_m = entropy(date.iloc[:, y])
        iv = entropy(condition_list)
        for i in indexs:
            _aim = date.iloc[(date[condition] == i).values, y]
            info_s += entropy(_aim) * len(_aim)/ total_length    
    elif ways =='gini':
        info_m = gini(date.iloc[:, y])
        iv = gini(condition_list)
        for i in indexs:
            _aim = date.iloc[(date[condition] == i).values, y]            
            info_s += gini(_aim) * len(_aim)/ total_length 
    else:
        print('无该方法') 
    gains = (info_m - info_s) / iv
    return gains

columns = train.columns
columns = columns.drop(['No', 'y'])
dic_gini = {}
for col in columns:
    gains = gain(train, col, ways = 'gini')
    print(f'{col}列的信息增益率为{gains}(基于基尼系数)')
    dic_gini[col] = gains
dic_entropy = {}
for col in columns:
    gains = gain(train, col)
    print(f'{col}列的信息增益率为{gains}（基于熵）')
    dic_entropy[col] = gains    
plt.rcParams['font.size']  = 20
fig = plt.figure(figsize = (16 ,9))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
rect1 = ax1.bar(dic_gini.keys(), dic_gini.values() )
for rec in rect1:
    x = rec.get_x()
    height = rec.get_height()
    ax1.text(x + 0.1,1.02 * height,'{:.3f}%'.format(height * 100), fontsize = 20)
rect2 = ax2.bar(dic_entropy.keys(), dic_entropy.values() )
for rec in rect2:
    x = rec.get_x()
    height = rec.get_height()
    ax2.text(x + 0.1,1.02 * height,'{:.3f}%'.format(height * 100), fontsize = 20)
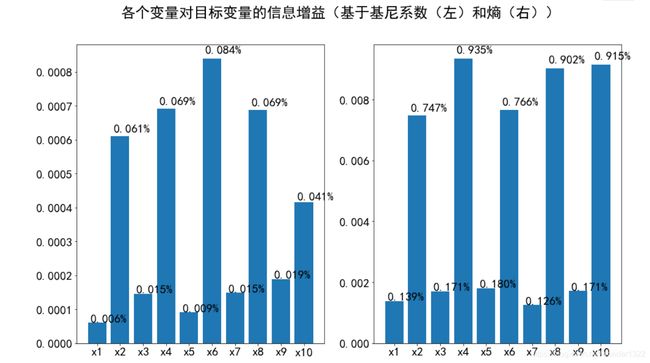
fig.suptitle('各个变量对目标变量的信息增益（基于基尼系数（左）和熵（右））')
plt.show()

columns = train.columns
columns = columns.drop(['No', 'y'])
dic_ratio_gini = {}
for col in columns:
    gains = gain_ratio(train, col, ways = 'gini')
    print(f'{col}列的信息增益率为{gains}(基于基尼系数)')
    dic_ratio_gini[col] = gains
dic_ratio_entropy = {}
for col in columns:
    gains = gain_ratio(train, col)
    print(f'{col}列的信息增益率为{gains}（基于熵）')
    dic_ratio_entropy[col] = gains    
plt.rcParams['font.size']  = 20
fig = plt.figure(figsize = (16 ,9))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
rect1 = ax1.bar(dic_ratio_gini.keys(), dic_ratio_gini.values() )
for rec in rect1:
    x = rec.get_x()
    height = rec.get_height()
    ax1.text(x + 0.1,1.02 * height,'{:.3f}%'.format(height * 100), fontsize = 20)
rect2 = ax2.bar(dic_ratio_entropy.keys(), dic_ratio_entropy.values() )
for rec in rect2:
    x = rec.get_x()
    height = rec.get_height()
    ax2.text(x + 0.1,1.02 * height,'{:.3f}%'.format(height * 100), fontsize = 20)
fig.suptitle('各个变量对目标变量的信息增益率（基于基尼系数（左）和熵（右））')
plt.show()

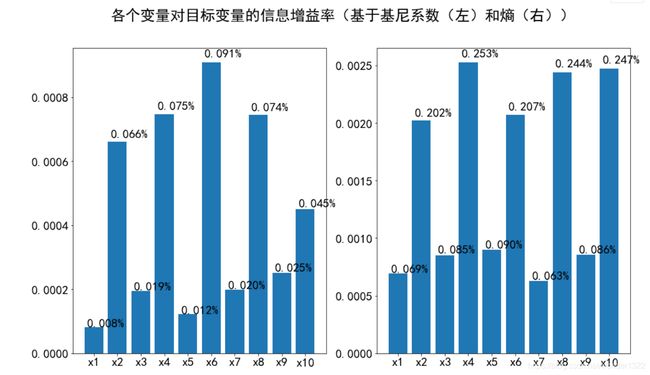
奇数列无论是信息增益，还是信息增益率都不及偶数列,不妨选择偶数列作为特征

train_x = train[['x2', 'x4', 'x6', 'x8', 'x10']]
train_y = train['y']
test_x = test[['x2', 'x4', 'x6', 'x8', 'x10']]

4.模型拟合

      1.logistic回归

## logistic回归
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(n_jobs = -1)
lr.fit(train_x,train_y)
score = (lr.predict(test_x) == true).mean()
score
# 结果为 0.49808256259869166

     2.决策树

# 决策树
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
dtc = DecisionTreeClassifier()
dtc.fit(train_x,train_y)
score = (dtc.predict(test_x) == true).mean()
score
## 0.533498759305211

     3.随机森林

# 随机森林
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc.fit(train_x,train_y)
score = (rfc.predict(test_x) == true).mean()
score
## 0.6352357320099256

     4.贝叶斯

# 贝叶斯
from sklearn.naive_bayes import GaussianNB,MultinomialNB,BernoulliNB
gnb = GaussianNB()
gnb.fit(train_x,train_y)
score = (gnb.predict(test_x) == true).mean()
score
# 0.49616512519738326

      5.其他一些模型

from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier(n_estimators=500, criterion='entropy',n_jobs = -1)
rfc.fit(train_x,train_y)
score = (rfc.predict(test_x) == true).mean()
score
# 0.6404240920369952

from sklearn.ensemble import ExtraTreesClassifier
etc = ExtraTreesClassifier()
etc.fit(train_x,train_y)
score = (etc.predict(test_x) == true).mean()
score
# 0.6281299345815475

from sklearn.ensemble import AdaBoostClassifier
abc = AdaBoostClassifier(n_estimators=100)
abc.fit(train_x,train_y)
score = (abc.predict(test_x) == true).mean()
score
# 0.48590119557861494

from sklearn.ensemble import GradientBoostingClassifier
gbd = GradientBoostingClassifier()
gbd.fit(train_x,train_y)
score = (gbd.predict(test_x) == true).mean()
score
# 0.6122264831942251

# pip install lightgbm
from lightgbm import LGBMClassifier
lgbm = LGBMClassifier()
lgbm.fit(train_x,train_y)
score = (lgbm.predict(test_x) == true).mean()
score
## 0.6443717572749831

lgbm = LGBMClassifier(n_estimators=250)
lgbm.fit(train_x,train_y)
score = (lgbm.predict(test_x) == true).mean()
score
# 0.673584480036093

from xgboost import XGBClassifier
xgb = XGBClassifier()
xgb.fit(train_x,train_y)
score = (xgb.predict(test_x) == true).mean()
score
# 0.728287841191067

特征减少之后过拟合现象有所减轻，最高的准确率可以到72%。这也突出了数据预处理、特征选择的必要性