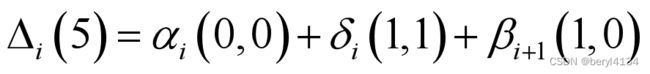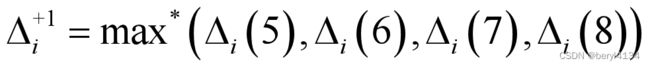(2,1,2)卷积码BCJR译码matlab仿真

---

前言

仿真(2,1,2)卷积码的性能，每个码块信息比特长度为1000，要求编码最终状态归0。要求输出的结果为译码后信息比特的BER。级联的调制方式采用QPSK。

(2,1,2)卷积码示意图

代码侧重于BCJR译码算法的编写过程

一、卷积码

1.1 卷积码状态转移图

黑色分支代表信息比特为0的状态转移分支,红色分支代表信息比特为1的状态转移分支。
假设在实际的传输过程中，0映射成-1,1映射成+1。

1.2 分支度量

卷积码基于接收比特似然比的分支计算：

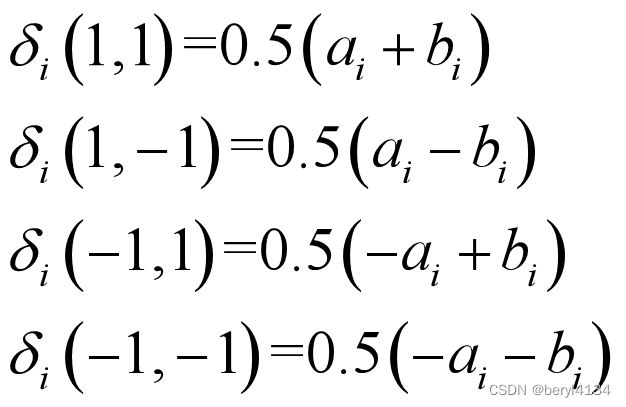第i级Trellis格图对应的分支为δi，在(2,1,2)编码中，每一个状态转移分支对应两个比特，假设从解调器获得的接收比特似然比分别为ai bi , 则对应不同分支的似然比可以根据以上公式计算

1.3 前向状态度量

第i级前向度量用αi表示，第i+1级前向度量用αi+1表示，基于第i级α度量计算第i+1级α度量。
前向状态度量计算示例(递推)

其中max*()运算如下，赋初值：

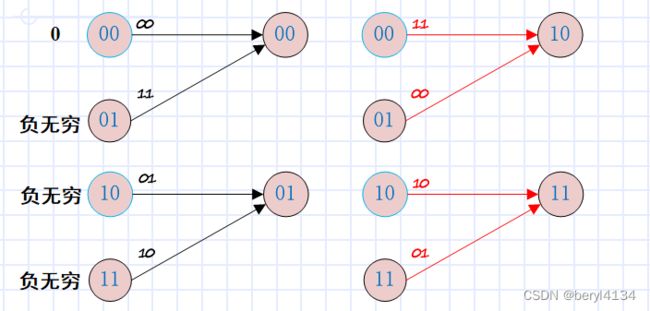
负无穷在实际的译码中可以取较大的负数值，例如可以取-1e6；
由于是前向度量，因此赋值是对第1级Trellis的4个状态赋值。

每个码块长1000比特，要求最终状态归0，需要1002比特(最后两位为0)，所以总的状态数位1003。但是第1003个状态的前向状态度量不会被使用。

每一步做归一化：
通过第i级前向状态度量可以计算得到第i+1级前向状态度量

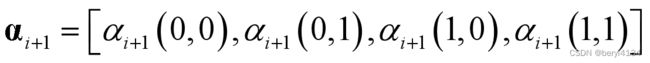
每一步进行归一化操作，以免溢出。

1.4 后向状态度量

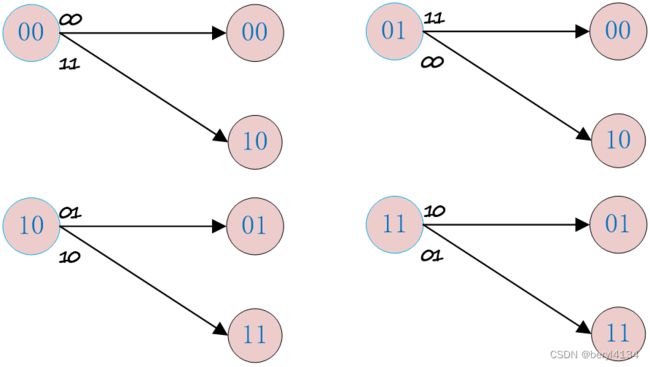
后向状态度量计算示例：
第i级前向度量用βi表示，第i+1级前向度量用βi+1表示，基于第i+1级β度量计算第i级β度量。

寄存器状态在最后需要归0，通过在发送序列最后补2个0，使得寄存器状态最终归0。第1个状态的后向状态度量也未被使用。

后向状态度量初值赋值：
负无穷在实际的译码中可以取较大的负数值，例如可以取-1e6，由于是后向度量，因此赋值是对最后1级Trellis的4个状态赋值。

后向状态度量每一步做归一化:
通过第i+1级后向状态度量可以计算得到第i级后向状态度量
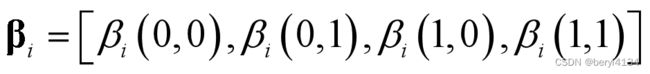
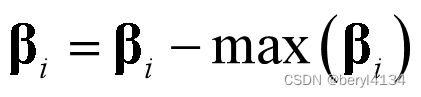每一步进行归一化操作

1.5 比特似然计算

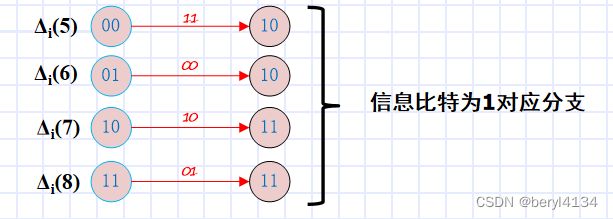
信息比特计算分组：
信息比特计算分组示例-1
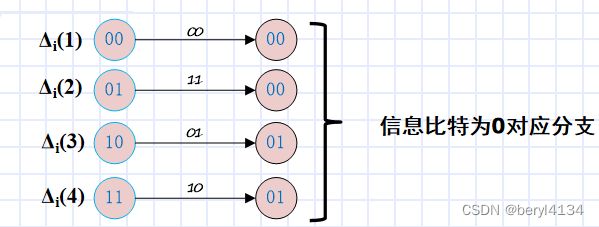
总的分支度量:

4个数求max*( )可以先将前2个数做一个max*()，得到的结果和第3个做max*()，然后得到的结果再和第4个做max*()。 也有其他方法，可查阅资料

信息比特计算分组示例-2
总的分支度量:

信息比特译码似然比

二、仿真代码

卷积码编码 -> QPSK调制 -> 通过高斯噪声信道 -> 接收端软解调

1.设置仿真参数

代码如下：

clear;
close all;
M = 4; % 调制方式QPSK
k = log2(M); % Bits/symbol
N = 1000; %每个码块信息比特长度
maxBitErrors = 100;    % 最大误比特数
maxNumBits = 1e6;      % 最大传输比特数

2.仿真所需系统对象

代码如下：

%设置QPSK调制和解调器，使它们接受二进制输入
qpskMod = comm.QPSKModulator("BitInput",true);
%qpskDemod = comm.QPSKDemodulator("BitOutput",true);
%将AWGN通道对象的NoiseMethod属性设置为Variance，并定义VarianceSource属性，以便可以从输入端口设置噪声功率。
channel = comm.AWGNChannel('NoiseMethod','Variance','VarianceSource','Input port');
%将ResetInputPort属性设置为true，以便在模拟期间重置错误率计算器。
errorRate = comm.ErrorRate('ResetInputPort',true);

3.定义星座点，用于计算软信息

a = -1/sqrt(2);

%定义星座点，用于计算软信息
cons_bit = zeros(k,M); %2行，4列的数组，每一列代表一个星座点
cons_sym = zeros(1,M);
cons_p = zeros(1,M);
for loop_modu = 1:1:k %星座点的实现
    temp_1 = [ones(1,2^(k-loop_modu)),-ones(1,2^(k-loop_modu))];
    cons_bit(loop_modu,:) = kron(ones(1,2^(loop_modu-1)),temp_1);
    clear temp_1
end
if k == 2  %假定第一列为虚部，第二列为实部
    cons_sym = a * (cons_bit(2,:) + 1i.*cons_bit(1,:)); %调制，格雷映射
    cons_p = abs(cons_sym).^2; %验证星座点功率,发送符号功率归一化p_ave=sum(cons_p)/2^Modu_t=1，峰值功率1.8；平均功率1；峰均比1.8
end

4.模拟通信链路

在Es/No值的范围内模拟通信链路，对于每个Es/No值，模拟运行直到记录maxBitErrors且传输的总位数超过maxNumBits。 ,横坐标步长为1dB

a = -1/sqrt(2);

%定义星座点，用于计算软信息
cons_bit = zeros(k,M); %2行，4列的数组，每一列代表一个星座点
cons_sym = zeros(1,M);
cons_p = zeros(1,M);
for loop_modu = 1:1:k %星座点的实现
    temp_1 = [ones(1,2^(k-loop_modu)),-ones(1,2^(k-loop_modu))];
    cons_bit(loop_modu,:) = kron(ones(1,2^(loop_modu-1)),temp_1);
    clear temp_1
end
if k == 2  %假定第一列为虚部，第二列为实部
    cons_sym = a * (cons_bit(2,:) + 1i.*cons_bit(1,:)); %调制，格雷映射
    cons_p = abs(cons_sym).^2; %验证星座点功率,发送符号功率归一化p_ave=sum(cons_p)/2^Modu_t=1，峰值功率1.8；平均功率1；峰均比1.8
end
在Es/No值的范围内模拟通信链路，对于每个Es/No值，模拟运行直到记录maxBitErrors且传输的总位数超过maxNumBits。 ,横坐标步长为1dB
%在符号信噪比0dB到5dB的情况下进行讨论
%根据所需的Es/No范围设置信噪比矢量。
EsN0_dB = (0:1:5)';
%初始化误码率和错误统计数组。
ber = zeros(length(EsN0_dB),3); %硬判决,comm.ErrorRate
errorStats = zeros(1,3);
%创建一个网格结构，以表示码率为1/2卷积编码器
trellis = poly2trellis(3,[5 7]) %记忆长度为3，生成多项式的二进制向量[101][111]分别表示八进制5，7

for snr = 0:1:5
    delta = zeros(4,N+2); %分支度量
    alpha = zeros(4,N+2); %前向状态度量，加上初始状态和结束状态一共有N+3个状态，但是结束状态的前向状态度量未被使用，未进行赋值
    beta = zeros(4,N+2);  %后向状态度量，初始状态的后向状态度量未被使用，未进行赋值
    Delta = zeros(8,N+2); %总的分支度量

    while errorStats(2) <= maxBitErrors || errorStats(3) <= maxNumBits
        data = randi([0 1],N,1); %生成二进制数据
        dataIn = [data' [0,0]]'; %使编码最终状态归零
        codedData = convenc(dataIn,trellis); %使用指定的网格结构对数据进行卷积编码
        qpskTx = qpskMod(codedData); %QPSK调制
      
        noiseVar = 10^(0.1*(-snr)); %计算噪声方差
        rxSig = channel(qpskTx,noiseVar); %通过高斯噪声信道
        

        %QPSK生成LLR的过程需要调用函数
        %获取接收比特似然比，参数：调制阶数、符号长度、星座点、星座点对应的比特序列、接收序列、噪声方差
        [llr_det] = euc_soft_sym_det(k,N+2,cons_sym,cons_bit,rxSig.',noiseVar); %A.'转置不共轭,A'共轭转置

        llr = reshape(llr_det,2,N+2);
        %计算分支度量(1-4行分别代表编码比特00,01,10,11)
        delta(1,:) = [-1,-1]*llr./2;
        delta(2,:) = [-1,1]*llr./2;
        delta(3,:) = [1,-1]*llr./2;
        delta(4,:) = [1,1]*llr./2;

        %计算前向状态度量(1-4行分别代表状态00,01,10,11)
        alpha(:,1) = [0,-10^6,-10^6,-10^6]'; %初始化第一列，默认初始状态为00
        for p = 2:1:N+2 %循环，每一次循环计算格图的一级
            %max*运算调用函数 max*(a,b) =  max(a,b)+log( 1 + exp( min(a,b)-max(a,b) ) )
            alpha(1,p) = max_(2,[alpha(1,p-1)+delta(1,p-1),alpha(2,p-1)+delta(4,p-1)]); %第一行，状态00
            alpha(2,p) = max_(2,[alpha(3,p-1)+delta(2,p-1),alpha(4,p-1)+delta(3,p-1)]); %状态01
            alpha(3,p) = max_(2,[alpha(1,p-1)+delta(4,p-1),alpha(2,p-1)+delta(1,p-1)]); %状态10
            alpha(4,p) = max_(2,[alpha(3,p-1)+delta(3,p-1),alpha(4,p-1)+delta(2,p-1)]); %状态11
            %每一步进行归一化操作
            alpha(:,p) = alpha(:,p)-max(alpha(:,p));
        end

        %计算后向状态度量(1-4行分别代表状态00,01,10,11)
        beta(:,N+2) = [0,-10^6,-10^6,-10^6]'; %初始化最后一列，默认初始状态为00
        for q = N+1:-1:1 %循环，每一次循环计算格图的一级
            %max*运算调用函数 max*(a,b) =  max(a,b)+log( 1 + exp( min(a,b)-max(a,b) ) )
            beta(1,q) = max_(2,[beta(1,q+1)+delta(1,q+1),beta(3,q+1)+delta(4,q+1)]); %第一行，状态00
            beta(2,q) = max_(2,[beta(1,q+1)+delta(4,q+1),beta(3,q+1)+delta(1,q+1)]); %状态01
            beta(3,q) = max_(2,[beta(2,q+1)+delta(2,q+1),beta(4,q+1)+delta(3,q+1)]); %状态10
            beta(4,q) = max_(2,[beta(2,q+1)+delta(3,q+1),beta(4,q+1)+delta(2,q+1)]); %状态11
            %每一步进行归一化操作
            beta(:,q) = beta(:,q)-max(beta(:,q));
        end

        %计算信息比特
        %计算总的分支度量，信息比特为0对应分支
        Delta(1,:) = alpha(1,:) + delta(1,:) + beta(1,:);
        Delta(2,:) = alpha(2,:) + delta(4,:) + beta(1,:);
        Delta(3,:) = alpha(3,:) + delta(2,:) + beta(2,:);
        Delta(4,:) = alpha(4,:) + delta(3,:) + beta(2,:);
        D0 = zeros(1,N+2);
        for t = 1:1:N+2
            D0(t) = max_(4,[Delta(1,t),Delta(2,t),Delta(3,t),Delta(4,t)]);
        end
        %信息比特为1对应分支
        Delta(5,:) = alpha(1,:) + delta(4,:) + beta(3,:);
        Delta(6,:) = alpha(2,:) + delta(1,:) + beta(3,:);
        Delta(7,:) = alpha(3,:) + delta(3,:) + beta(4,:);
        Delta(8,:) = alpha(4,:) + delta(2,:) + beta(4,:);
        D1 = zeros(1,N+2);
        for r = 1:1:N+2
            D1(r) = max_(4,[Delta(5,r),Delta(6,r),Delta(7,r),Delta(8,r)]);
        end

        %信息比特译码似然比
        L = D1-D0;

        %信息比特的似然比(若取+1的概率大于取-1的概率，LLR为正，反之为负)
        output = (sign(L)+1)/2; %判断正负,将-1,+1映射到0,1

        %统计误比特率
        errorStats = errorRate(dataIn,output',0);  %收集错误统计数据

      
    end
    ber(snr+1,:) = errorStats; %保存BER数据
    errorStats = errorRate(dataIn,output',1);%重置错误率计算器

end

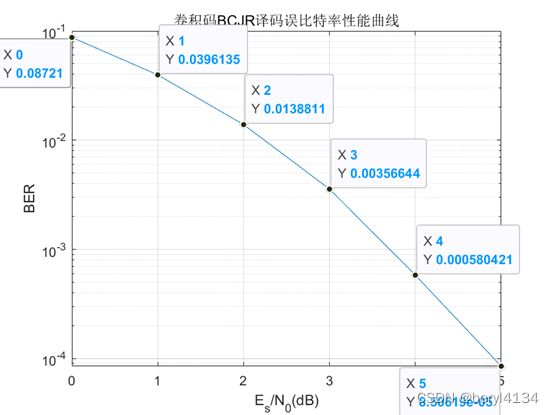
1.5 仿真结果图

semilogy(EsN0_dB,ber(:,1),'-*'); %对数函数，Es_N0单位为dB
title('卷积码BCJR译码误比特率性能曲线');
xlabel('E_s/N_0(dB)');
ylabel('BER');
grid

1.6 自定义接收比特似然比函数

%解调的软信息，可求比特的似然比
function [llr_det] = euc_soft_sym_det(Modu_t,N_sample,cons_sym,cons_bit,s_con_mat,sigma_hard)
%参数:Modu_t调制阶数，N_sample解调的符号长度，cons_sym星座点(const)，(const)cons_bit星座点bit序列，s_con_mat接收信号，sigma_hard噪声方差
euc_det = zeros(2^Modu_t,N_sample); %欧氏距离(对于每一个符号，都要计算其与每一个星座点的欧式距离)
for loop_modu_det = 1:1:2^Modu_t 
    %每一次循环计算所有的符号到一个某一个星座点的欧氏距离，按行计算
    euc_det(loop_modu_det,:) = - abs( s_con_mat - cons_sym(1,loop_modu_det)).^2./sigma_hard;
end
llr_det = zeros(1,Modu_t*N_sample);

if Modu_t == 2  %调制阶数为2,QPSK
    for loop_llr_det = 1:1:N_sample %外层循环，对每一个符号进行判决
        for loop_llr_bit = 1:1:Modu_t %遍历星座点每一个比特
            ind_temp_plus = cons_bit(loop_llr_bit,:) == 1; %符号星座点第loop_llr_bit个比特为+1的序号
            ind_temp_minus = cons_bit(loop_llr_bit,:) == -1;
            a_temp_plus = euc_det(ind_temp_plus,loop_llr_det);
            a_temp_minus = euc_det(ind_temp_minus,loop_llr_det);
            llr_det(1,(loop_llr_det-1)*Modu_t+loop_llr_bit) = max(a_temp_plus)+log(sum(exp(a_temp_plus-max(a_temp_plus))))-max(a_temp_minus)-log(sum(exp(a_temp_minus-max(a_temp_minus))));
            %这里euc_det是负数，本来不易溢出，但这样计算更不容易溢出
        end
    end
end

1.7 自定义max*()函数

这个函数写复杂了，可以省略num这个参数，num可以用list.length得到。

%max*函数，递归函数
function log_max = max_(num,list)
%参数：num输入的个数，list待比较的数组
if num == 2
    a = list(1); b = list(2);
    log_max = max(a,b)+log( 1 + exp( min(a,b)-max(a,b) ) );
else
    log_max = max_(2,[list(num),max_(num-1,list(1:num-1))]);
end
    
end

三、仿真结果

Es_N0(dB)	BER	误比特数	传输比特数
0	0.087209964	87297	1000998
1	0.039613466	39653	1000998
2	0.013881147	13895	1000998
3	0.003566441	3570	1000998
4	0.000580421	581	1000998
5	8.51E-05	101	1187370

---

总结

仿真结果图如上，随着符号信噪比Es_N0的增加，误比特率BER降低。在信噪比为5dB时，误比特率BER达到10^-4量级，说明使用BCJR算法对卷积码进行译码的误码性能较好。