matlab卷积画图,基于MATLAB的卷积演示系统课程设计

1卷积演示程序设计原理

数字信号处理的直接对象是数字信号，处理的方式是数值运算的方式，它涉及到的内容非常丰富和广泛，它是应用最快、成效最显著的新学科之一，作为信息专业的专业基础课，需要掌握其基本理论和基本的分析方法，通过理论实践、原理和应用结合掌握知识。而MATLAB是集数学计算、图形处理和程序语言设计于一体的软件，通过MATLAB来实现数字信号处理的有关表达，最终实现课程设计的目的。卷积演示程序设计要求

(1)序列的长度和内容由运行时输入；

(2)分别动态演示它们进行线性卷积和循环卷积的过程，要求体现翻转、移位、相乘、求和等过程；

(3)根据卷积结果，分析两类卷积的关系。卷积演示程序设计目的

(1)、通过基于MATLAB的算法仿真实验及分析，进一步领会和深化课堂上学到的有关数字信号处理的基本概念、基本原理以及基本的信号处理操作及设计方法。

(2)、掌握线性卷积与圆周卷积软件实现的方法，并验证二者之间的关系。

1.2 卷积演示程序设计内容

(1)可输入任意2待卷积序列x1(n)、x2(n)，长度不做限定。测试数据为：

x1(n)={1,1,1,1,0, 0,1,1,1,1,0,0}，x2(n)={0,1,2,1,0,0,0,1,2,1,0,0}；

(2)分别动态演示2序列进行线性卷积x1(n)﹡x2(n)和圆周卷积x1(n) x2 (n)的过程；要求分别动态演示翻转、移位、乘积、求和的过程。

(3)圆周卷积默认使用2序列中的最大长度，但卷积前可以指定卷积长度N用以进行混叠分析。

(4)根据实验结果分析2类卷积的关系。

2卷积演示程序总体设计及关键技术分析

2.1 卷积演示程序设计基本原理

2.1.1 线性卷积

线性时不变系统(Linear Time-Invariant System, or L. T. I系统)的输入、输出间的关系为：当系统输入序列为x(n)，系统的单位脉冲响应为h(n)，输出序列为y(n)，则系统输出为：

或

上式称为离散卷积或线性卷积。

2.1.2 圆周卷积

设两个有限长序列x1(n)和x2(n)，均为N点长

x1(n)

X1(K)

x2(n)

X2(K)

如果X3(K)=X1(K)﹒X2(K)

则

N

上式称为循环卷积或圆周卷积

注：

为x1(n)序列的周期化序列；

为

的主值序列。

编程计算时，x3(n)可表示如下：

2.2 两个有限长序列的线性卷积

序列x1(n)为L点长，序列x2(n)为P点长，x3(n)为这两个序列的线性卷积，则x3(n)为

且线性卷积x3(n)的最大长L+P-1，也就是说当

和

时x3(n)=0。

2.3 两个有限长序列的圆周卷积

线性卷积是求离散系统响应的主要方法之一，许多重要应用都建立在这理论基础上，如卷积滤波等，专用函数conv(x,h)可完成线性卷积过程。

圆周卷积的计算速度远快于线性卷积，如果选择圆周卷积的长度

,则可以用圆周卷积取代线性卷积。方法如下：定义圆周卷积的长度：选择N=L+P-1。

将两个序列的长度都补足为N:

将长为L的序列x1(n)延长到N，补N-L个零；

将长为P的序列x2(n)延长到N，补N-P个零；翻转x1(n)，周期延拓为序列

，取主周期。

循环移位：与线性卷积不同，圆周卷积运算中采用的是循环移位，有限长序列x1(n)的循环移位定义为：

其含义如下：

表示x(n)的周期延拓序列

的移位：



表示对移位的周期序列

取主值序列。所以f(n)仍然是一个长度为N的有限长序列。

2.4 卷积演示程序设计思想

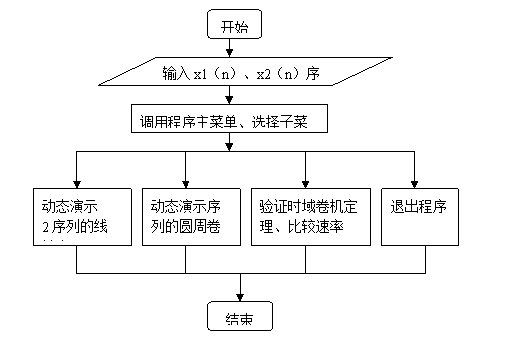
首先建立一个基本的框架，制作一个菜单，其中包括主程序菜单和子程序的菜单，子程序菜单可以选择回到主程序菜单选择功能。菜单的框架完成后，实现可以任意输入两个序列，然后分别制作动态演示序列的线性卷积的程序、动态演示序列的圆周卷积、以及验证时域卷机定理以及比较运行速率的程序。结合上面建立的框架完成菜单选择以及功能的调用，让整个设计完美。

2.4.1卷积演示程序设计流程图

卷积演示程序设计流程图如图1所示：

图1  流程图

2.4.2卷积演示程序关键技术分析

本个设计主要要实现动态的演示，为实现动态演示，有很多不同的方法，而我采用的是for循环加上pause，在for循环中的一次执行中，实现一次绘图，表示某一时刻的状态，用pause暂停等待for循环中下一次执行，实现动态演示。这是主要的一个设计，另外一个重要的技巧是如何将循环卷积表示出来，因为循环卷积的结果是周期的，其循环卷积的方法和线性卷积不同，并且循环卷积中要处理几种情况：如当x1序列和x2序列之间的最大长度比卷积N长度大时是一种画图方法，比它小时是另外一种方法，然而困难的是当循环卷积长度比序列最大长度小时还要分析x1和x2序列各自长度与N的关系而做不同的情况分析，具体的解决方法见程序实现。

3卷积演示程序

3.1程序实现

3.1.1线性卷积程序实现

x1=[1,1,1,1,0,0,1,1,1,1,0,0];

x2=[0,1,2,1,0,0,0,1,2,1,0,0];

p=length(x1);

q=length(x2);

n=p+q-1;

a= 0 : q-1;

y2(a+1)=x2(q-a);

for n=1 : p+q-1

k=-q+n:1:-1+n;

subplot(3,1,2)

stem(k,y2)

title('x2(n-m)');

axis([-16,16,0,24]);

以上部分是实现翻转并移位，在设计中是将序列x2进行翻转和移位。

y=conv(x1,x2);

t=1:1:n

h(t)=y(t);

subplot(3,1,3)

t=0:n-1;

stem(t,h);

title('线性卷积y(n)')

axis([-16,16,0,24]);

pause(1)

end

以上整个部分就是实现线性卷积的过程。

subplot(3,2,1)

stem(x1);

title('x1(m)')

axis([0,15,0,1]);

pause(1)

subplot(3,2,2)

stem(x2);

title('x2(m)')

axis([0,15,0,2]);

pause(1)

end

3.1.2圆周卷积程序实现

对于循环卷积，要求我们进行判断并根据情况做不同的分析：

x1=[1,1,1,1,0,0,1,1,1,1,0,0];

x2=[0,1,2,1,0,0,0,1,2,1,0,0];

p=length(x1);q=length(x2);k=max(p,q);%p

if k>N

if p

x11=[x1,zeros(1,N-p)];

n=0:1:N-1;

x22(n+1)=x2(n+1);

elseif p==q|p>N

n=0:1:N-1;

x11(n+1)=x1(n+1);

x22(n+1)=x2(n+1);

else disp('错误，x1的长度要比x2短')

end

3.2结果及分析

开始运行程序，会进入主菜单，按照提示进行选择：

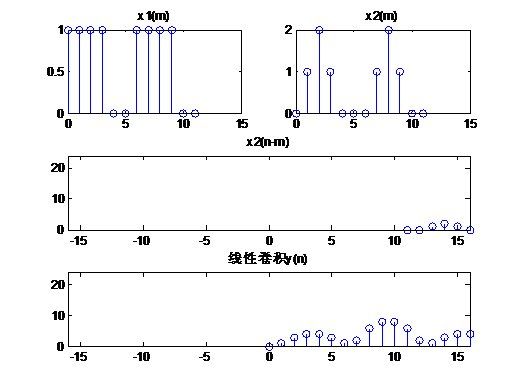
请输入x1:[1,1,1,1,0,0,1,1,1,1,0,0]

请输入x2:[0,1,2,1,0,0,0,1,2,1,0,0]

(1)、动态演示2序列的线性卷积

图2   线性卷积结果

(2)、动态演示2序列的10点的圆周卷积

图3  圆周卷积结果

4结论

针对卷积演示的程序进行设计，并给出了两个示例序进行线性卷积和圆周卷积的翻转、移位、乘机、求和的过程等。圆周卷积是将所有数据限定一个固定的长度。设线性卷积和圆周卷积有用信号部分长度分别为L、P，则当圆周卷积长度大于等于L+P-1时两者等价。

线性卷积和圆周卷积对运算有不同的要求：线性卷积的对象可以是有限长或无限长非周期序列，若两个序列的长度分别为M和N，则卷积后的序列长度为L=M+N-1。圆周卷积的对象是两个同长度(若长度不同可用补零的方法达到同长度)的有限长序列，圆周卷积的结果也是同一长度的有限长序列。

它们的关系是：圆周卷积是线性卷积L点周期延拓的主值区间。

5心得体会

通过本次论文设计巩固了所学过的数字信号处理课程的有关知识，同时也对matlab这个软件有了更深的了解，它与数字信号处理这门课程之间有着紧密关系，matlab中是采用数组和距阵的方式处理数据，如何将数字信号处理有关的资料以数组和距阵进行编程是我们学习的一个方面，通过这次的课程设计，让我发现了数字信号处理在matlab中的应用，同时也激发了我利用这软件来实现数字信号处理有关问题的兴趣。

本次设计中，有机地结合了理论与实践，既考察了我们对理论知识的掌握情况，还反映出我们实际动手能力和编程能力，更主要的是它激起我们创新思维，提高了自己独立分析问题和解决问题的能力，这在无形中以及提高了我各方面的能力。无论是在知识上，还是在思想上都给我烙下了深刻的印象。

完整的Word格式文档51黑下载地址：

2018-6-22 17:02 上传

点击文件名下载附件

下载积分: 黑币 -5