机器学习——聚类——商场客户聚类

聚类的介绍

…………………………………………

…………………………………………

案例——商场客户聚类

目录

聚类的介绍

案例——商场客户聚类

一、读取数据

二、聚类

KMeans函数的参数讲解：

KMeans属性列表

KMeans接口列表​

三、查看数据及可视化

sort_values（）方法

groupby（）的常见用法

 groupby（）的配合函数

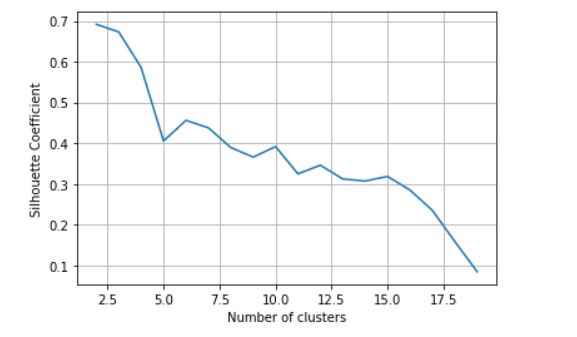
 四、聚类评价指标。计算聚簇数量从2到19时的轮廓系数。

---

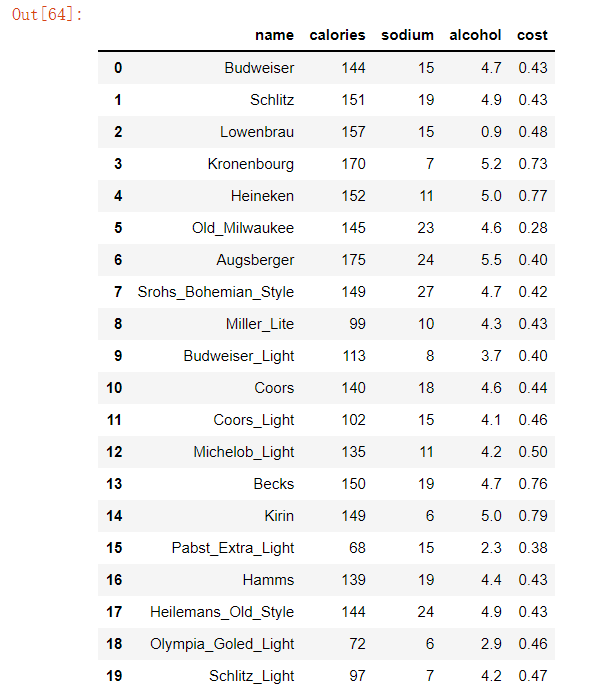
一、读取数据

import pandas as pd 
beer=pd.read_csv('beer.txt',sep=' ')
#输出文件内容
beer

pandas.read_csv

常用参数为：header, sep, name……

header(表头)：

指定行数用来作为列名，数据开始行数。

如果文件中没有列名，则默认为0，否则设置为None。如果明确设定header=0 就会替换掉原来存在列名。

header参数可以是一个list例如：[0,1,3]，这个list表示将文件中的这些行作为列标题（意味着

每一列有多个标题），介于中间的行将被忽略掉（例如本例中的2；本例中的数据1,2,4行将被作为多级标题出现，第3行数据将被丢弃，dataframe的数据从第5行开始）。

注意：如果skip_blank_lines=True 那么header参数忽略注释行和空行，所以header=0表示第一

行数据而不是文件的第一行。
 

sep(分隔符)：

​ 指定分隔符。如果不指定参数，则会尝试使用逗号分隔。分隔符长于一个字符并且不是‘\s+’,

将使用python的语法分析器。并且忽略数据中的逗号。正则表达式例子：’\r\t’

 names(列名)：

用于结果的列名列表，如果数据文件中没有列标题行，就需要执行header=None。默认列表中不

能出现重复，除非设定参数mangle_dupe_cols=True。

二、聚类。把除name之外的所有属性当作输入特征

name 为离散型，所有使用drop删除此行，剩下的为连续性数据

n_clusters：初始化一个3个的聚簇

random_state：及初始化生成的3个聚簇进行标记
确定质心初始化的随机数生成。使用int可以使随机性具有确定性。 确定质心初始化的随机数生成.使用int可以使随机性具有确定性.

fit训练过程：

1.（随机）选择K个聚类的初始中心；

2.对任意一个样本点，求其到K个聚类中心的距离，将样本点归类到距离最小的中心的聚类，如此迭代n次；

3.每次迭代过程中，利用均值等方法更新各个聚类的中心点(质心)；

4.对K个聚类中心，利用2,3步迭代更新后，如果位置点变化很小(可以设置阈值)，则认为达到稳定状态，迭代结束，对不同的聚类块和聚类中心可选择不同的颜色标注。
 

#准备输入特征X
X=beer.drop('name',axis=1)
from sklearn.cluster import KMeans
km=KMeans(n_clusters=3,random_state=1)
km.fit(X)

drop函数的使用：删除行、删除列：

参数名称	参数取值	参数意义
axis	0 or ‘index’, 1 or ‘columns’ , default 0	确定是删除包含缺失值的行还是列
how	‘any’ or ‘all’, default ‘any’	表明是至少存在一个NAN值还是全为NAN值时执行删除操作
thresh	int, 可选	指定存在多少个NAN值才进行删除操作
subset	array, 可选	可选子集列表
inplace	bool, default False	如果为真，执行inplace操作，并返回None

KMeans函数的参数讲解：

1、n_clusters : 聚类中心数量（开始时需要产生的聚类中心数量），默认为8

2、max_iter : 算法运行的最大迭代次数，默认300

3、tol: 容忍的最小误差，当误差小于tol就会退出迭代（算法中会依赖数据本身），默认为1e-4

4、n_init : k-means算法会随机运行n_init次，最终的结果将是最好的一个聚类结果，默认10

5、init : 聚类中心的初始化方案，有三个选择{'k-means++', 'random' or an ndarray}

  5.1、 'k-means++' : 默认选项，初始化过程如下

（1）、从输入的数据点集合（要求有k个聚类）中随机选择一个点作为第一个聚类中心；

（2）、对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)；

（3）、选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大；（4）、重复2和3直到k个聚类中心被选出来

  5.2、'random': 随机选择k个实例作为聚类中心

  5.3、ndarray：如果传入为矩阵（ndarray），则将该矩阵中的每一行作为聚类中心

6、algorithm :可选的K-means距离计算算法， 可选{"auto", "full" or "elkan",default="auto"}

       6.1"full"：传统的距离计算方式.

       6.2"elkan"：使用三角不等式，效率更高，但是目前不支持稀疏数据。1、计算任意两个聚类中心的距离；2当计算x点应该属于哪个聚类中心时，当发现2*S(x，K1)S(x，K1)，

       6.3"auto"：当为稀疏矩阵时，采用full，否则elkan。

7、precompute_distances : 是否将数据全部放入内存计算，可选{'auto', True, False}，开启时速度更快但是更耗内存.

       7.1、'auto' : 当n_samples * n_clusters > 12million，不放入内存，否则放入内存，double精度下大概要多用100M的内存

       7.2、True : 进行预计算

       7.3、False : 不进行预计算

8、n_jobs : 同时进行计算的核数（并发数），n_jobs用于并行计算每个n_init，如果设置为-1，使用所有CPU，若果设置为1，不并行，如果设置小于-1，使用CPU个数+1+n_jobs个CPU

9、random_state : 用于随机产生中心的随机序列

10、verbose : 是否输出详细信息，默认为0，bush

11、copy_x : 是否直接在原矩阵上进行计算。默认为True，会copy一份进行计算。

KMeans属性列表

KMeans接口列表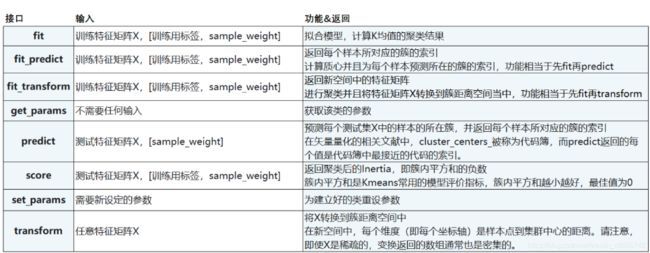

三、查看数据及可视化

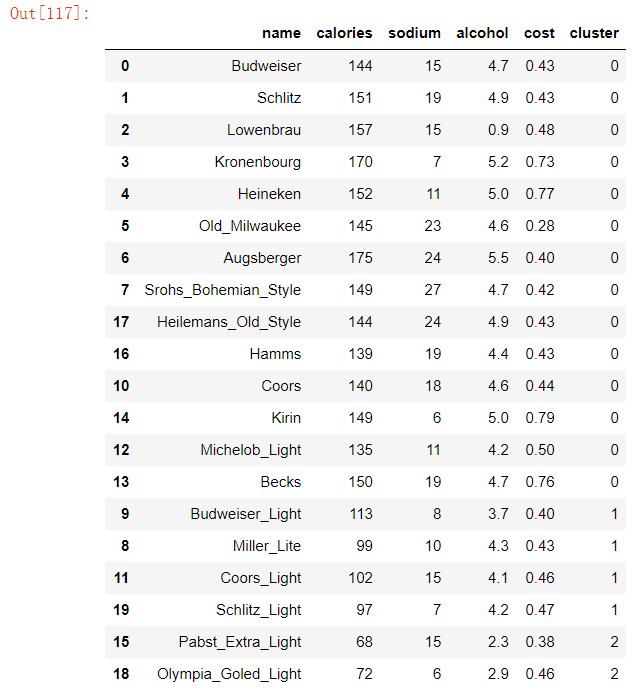
在表beer中添加一列cluster放入标签数据，km.labels_每个样本点对应的标签，并进行升序排序

beer['cluster']=km.labels_
beer.sort_values(by='cluster')

sort_values（）方法

sort_values(by, axis=0, ascending=True, inplace=False, kind=‘quicksort’, na_position=‘last’)

参数	含义
axis	如果axis=0，那么by=“列名”； 如果axis=1，那么by=“行名”；
ascending	True则升序，可以是[True,False]，即第一字段升序，第二个降序
inplace	是否用排序后的数据框替换现有的数据框 ，True,或者False
kind	排序方法
na_position	{‘first’, ‘last’}, default ‘last’，默认缺失值排在最后面

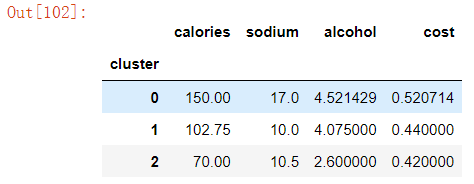
 查看每个聚类的每维特征上的平均值（即聚簇中心点）

centers=beer.groupby('cluster').mean()
centers

groupby（）的常见用法

函数	适用场景	备注
df.groupby(‘key1’)	一列聚合	分组键为列名（可以是字符串、数字或其他Python对象）
df.groupby([‘key1’,‘key2’])	多列聚合	分组键为列名，引入列表list[]
df[‘data1’].groupby(df[‘key1’]).mean()	按某一列进行一重聚合求均值	分组键为Series
A=df[‘订单编号’].groupby([ df[‘运营商’], df[‘分类’], df[‘百度圣卡’] ]).count()	按某一列进行多重聚合计数	分组键为Series，引入列表list[]
df[‘data1’].groupby([states,years]).mean()	分组键与原df无关，而是另外指定的任何长度适当的数组	分组键是数组，state和year均为数组

 groupby（）的配合函数

函数	适用场景	备注
.mean()	均值
.count()	计数
.min()	最小值
.mean().unstack()	求均值，聚合表的层次索引不堆叠
.size()	计算分组大小	GroupBy的size方法，将返回一个含有分组大小的Series
.apply()
.agg()

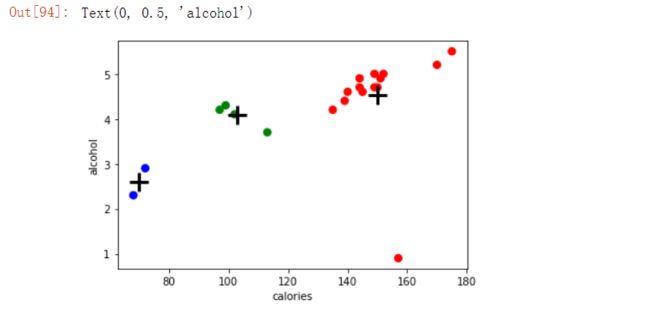
#可视化
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
colors =np.array(['red','green','blue','yellow'])
plt.scatter(beer.calories,beer.alcohol,c=colors[beer.cluster],s=50)
plt.scatter(centers.calories,centers.alcohol,linewidths=3,marker='+',s=300,c='black')
plt.xlabel('calories')
plt.ylabel('alcohol')

 四、聚类评价指标。计算聚簇数量从2到19时的轮廓系数。

from sklearn import metrics
k_range=range(2,20)
scores=[]
for k in k_range:
    km=KMeans(n_clusters=k,random_state=1)
    km.fit(X)
    scores.append(metrics.silhouette_score(X,km.labels_))
plt.plot(k_range,scores)
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Coefficient')
plt.grid(True)

聚类性能评估-轮廓系数 - 知乎

轮廓系数（Silhouette Coefficient）

是聚类效果好坏的一种评价方式。轮廓系数取值范围为[-1,1]，取值越接近1则说明聚类性能越好，相反，取值越接近-1则说明聚类性能越差。

a：某个样本与其所在簇内其他样本的平均距离
b：某个样本与其他簇样本的平均距离
针对某个样本的轮廓系数s为：

聚类总的轮廓系数SC为：

轮廓系数的优点：

轮廓系数为-1时表示聚类结果不好，为+1时表示簇内实例之间紧凑，为0时表示有簇重叠。
轮廓系数越大，表示簇内实例之间紧凑，簇间距离大，这正是聚类的标准概念。

轮廓系数的缺点：

对于簇结构为凸的数据轮廓系数值高，而对于簇结构非凸需要使用DBSCAN进行聚类的数据，轮廓系数值低，因此，轮廓系数不应该用来评估不同聚类算法之间的优劣，比如Kmeans聚类结果与DBSCAN聚类结果之间的比较。
根据折线图可直观的找到系数变化幅度最大的点，认为发生畸变幅度最大的点就是最好的聚类数目。
 

完整代码：

import pandas as pd 
beer=pd.read_csv('beer.txt',sep=' ')
beer

#准备输入特征X
X=beer.drop('name',axis=1)
from sklearn.cluster import KMeans
km=KMeans(n_clusters=3,random_state=1)
km.fit_predict(X)

beer['cluster']=km.labels_
beer.sort_values(by='cluster')

centers=beer.groupby('cluster').mean()
centers

#可视化
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
colors =np.array(['red','green','blue','yellow'])
plt.scatter(beer.calories,beer.alcohol,c=colors[beer.cluster],s=50)
plt.scatter(centers.calories,centers.alcohol,linewidths=3,marker='+',s=300,c='black')
plt.xlabel('calories')
plt.ylabel('alcohol')

from sklearn import metrics
k_range=range(2,20)
scores=[]
for k in k_range:
    km=KMeans(n_clusters=k,random_state=1)
    km.fit(X)
    scores.append(metrics.silhouette_score(X,km.labels_))
plt.plot(k_range,scores)
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Coefficient')
plt.grid(True)

---

今天看到了一句话：

当你已经差到谷底的时候，已经不能再差了，那无论你做什么，都是在走上坡路。

努力奋斗，你行滴！

点个小♥