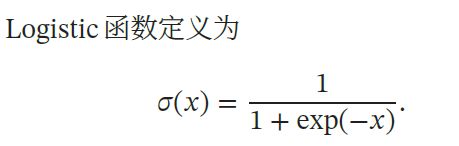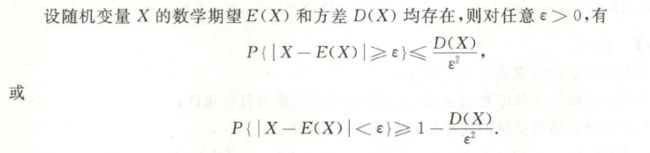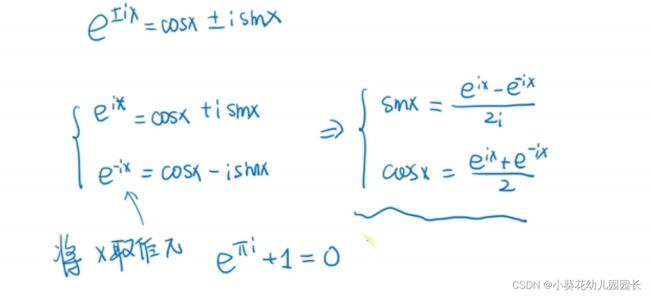算法工程师（机器学习）面试题目2---数学基础

说明：这些是自己整理回答的答案 可以借鉴 也可能存在错误 欢迎指正

数学基础

1. 微积分

1.1 SGD,Momentum,Adagard,Adam原理

SGD（Stochastic Gradient Decent）随机梯度下降

• 在批量梯度下降法（Batch Gradient Descent，BGD）的基础上改进，批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和（空间复杂度高，计算开销大）。
• 为了减少每次迭代的计算复杂度。在每次迭代时只采集一个样本，计算这个样本损失函数的梯度并更新参数----随机梯度下降法（增量梯度下降法）。

当经过足够次数的迭代时，也可以收敛到局部最优解

Momentum（动量）

动量（Momentum）是模拟物理中的概念，一个物体的动量指的是该物体在它运动方向上保持运动的趋势，是该物体的质量和速度的乘积

• 动量法（Momentum Method）是用之前积累动量来替代真正的梯度。每次迭代的梯度可以看作加速度。

这样，每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值。
当某个参数在最近一段时间内的梯度方向不一致时，其真实的参数更新幅度变小；
相反，当在最近一段时间内的梯度方向都一致时，其真实的参数更新幅度变大，起到加速作用。
在迭代后期，梯度方向会不一致，在收敛值附近振荡，动量法会起到减速作用，增加稳定性

AdaGard（Adaptive Gradient Algorithm）

在标准的梯度下降法中，每个参数在每次迭代时都使用相同的学习率．由于每个参数的维度上收敛速度都不相同，因此根据不同参数的收敛情况分别设置学习率．

• 每次迭代时自适应地调整每个参数的学习率．

在AdaGrad 算法中，如果某个参数的偏导数累积比较大，其学习率相对较小；相反，如果其偏导数累积较小，其学习率相对较大．但整体是随着迭代次数的增加，学习率逐渐缩小．

AdaGrad 算法的缺点是在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点．

Adam（Adaptive Moment Estimation Algorithm）

动量法和RMSprop算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率

1.2 L1不可导的时候该怎么办

当损失函数不可导时，梯度下降算法不再有效，可以使用坐标轴下降法进行求解。

梯度下降法： 沿着当前点的负梯度方向进行参数更新
坐标轴下降法：沿着坐标轴的方向进行参数更新

1.3 sigmoid函数特性

常用的Sigmoid型函数有Logistic 函数和Tanh 函数．

特性：

1. “挤压”函数，把一个实数域的输入“挤压”到一定范围内（Logistics—（0,1）；Tanh—（-1,1））
2. 当输入值在0 附近时，Sigmoid 型函数近似为线性函数；当输入值靠近两端时，对输入进行抑制。输入越小，越接近于0；输入越大，越接近于1。（Logistics为例）

2. 概率论

2.1 a,b~U[0,1]，互相独立,求Max(a,b)期望

2.2 问题：

一个活动,n个女生手里拿着长短不一的玫瑰花,无序的排成一排,一个男生从头走到尾,试图拿更长的玫瑰花,一旦拿了一朵就不能再拿其他的,错过了就不能回头,问最好的策略?

可以参考：37%

37%法则

2.3 问题：

某大公司有这么一个规定：只要有一个员工过生日，当天所有员工全部放假一天。但在其余时候，所有员工都没有假期，必须正常上班。这个公司需要雇用多少员工，才能让公司一年内所有员工的总工作时间期望值最大？

365个人

2.4 切比雪夫不等式

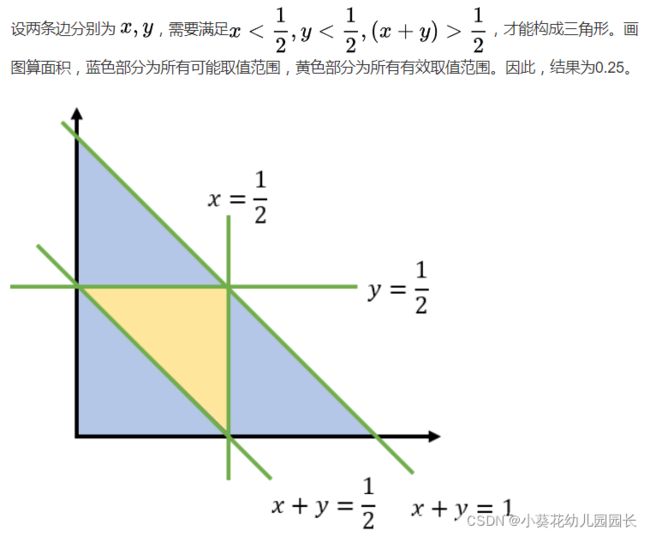
2.5 一根绳子,随机截成3段,可以组成一个三角形的概率有多大

2.6 最大似然估计和最大后验概率的区别?

最大似然估计（Maximum likelihood estimation, 简称MLE）
最大后验概率估计（Maximum a posteriori estimation, 简称MAP）

最大似然函数

似然函数描述的是在已知一种模型下，针对某个参数，观察到了一种抽样结果（或者说有了一种观察到的结果）的概率函数 【即：特定分布模型下，观察值x在给定某参数sita下的条件概率函数）

求最大似然估计，就是去求参数sita应该取什么值的时候能够让如上所说的条件概率最大，也就是这种观察发生的概率最大。

最大后验概率

最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似，但是最大的不同时，最大后验估计的融入了要估计量的先验分布在其中。故最大后验估计可以看做规则化的最大似然估计。
特点：

1. 概率函数。是在已知模型，已知关于某参数sita的先验知识（分布），以及基于该参数得到抽样或观察结果x的条件概率分布等条件下，描述在已经观察到某抽样或已经得到了某观察结果的条件下，该参数的分布概率情况；

2. 考虑了特定模型的自身分布情况，也就是考虑了先验分布概率。

3. 利用了贝叶斯定理，是贝叶斯公式最重要的实际应用之一。是通过已知的先验知识和观察到的实际结果，对知识进行更新的过程。

2.7 什么是共轭先验分布

2.8 概率和似然的区别

概率（Probability）
似然（Likelihood）

概率

概率研究的问题是，已知一个模型和参数，怎么去预测这个模型产生的结果的特性（例如均值，方差，协方差等等）。

举个例子，我想研究怎么养猪（模型是猪），我选好了想养的品种、喂养方式、猪棚的设计等等（选择参数），我想知道我养出来的猪大概能有多肥，肉质怎么样（预测结果）。

似然

似然函数(通常简称似然)是参数空间内参数的函数，描述获得观测数据的概率。

统计推断则根据观测的数据，反向思考其数据生成过程。预测、分类、聚类、估计等，都是统计推断的特殊形式，强调对于数据生成过程的研究

2.9 频率学派和贝叶斯学派的区别

贝叶斯学派和频率学派的区别之一是

• 特别重视先验信息对于inference的影响
  贝叶斯公式：做判断的时候，要考虑所有的因素。

贝叶斯学派的思想了——要考虑先验概率

2. 10 Lasso的损失函数（L1正则化）

Lasso(Least absolute shrinkage and selection operator)
基于回归系数的一范数

• 将变量的系数进行压缩并使某些回归系数变为0，进而达到变量选择的目的

2.11 Sfit特征提取和匹配的具体步骤

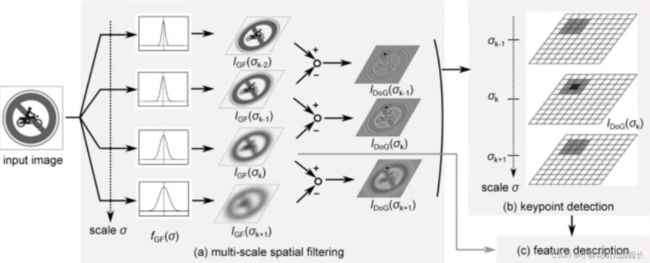
Sift（尺度不变特征变换）Scale Invariant Feature Transform
Sfit算法的实质是在不同的尺度空间上查找关键点（特征点），计算关键点的大小、方向、尺度信息，利用这些信息组成关键点对特征点进行描述的问题。

Sfit特征提取和匹配具体步骤

1. 尺度空间极值检测

   搜索所有尺度上的图像位置。通过高斯差分函数来识别潜在的对于尺度和旋转不变的关键点。
   

2. 关键点定位

   在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度

3. 关键点方向确定、方向赋值

   基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而保证了对于这些变换的不变性。

4. 关键点描述

   在每个关键点周围的领域内，在选定的尺度上测量图像局部的梯度。这些梯度作为关键点的描述符，它允许比较大的局部形状的变形或光照变化。

3. 线性代数

3.1、求mk矩阵A和nk矩阵的欧几里得距离?

向量的欧式距离

矩阵距离

3.2、PCA中第一主成分是第一的原因?

主成分分析（Principal Component Analysis，PCA）是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

主成分一：方差最大，能够保留最多的信息

3.3、欧拉公式

视频讲解：欧拉公式

推导

3.4、矩阵正定性的判断,Hessian矩阵正定性在梯度下降中的应用

矩阵正定性判断

矩阵正定性的性质：
1、正定矩阵的特征值都是正数。
2、正定矩阵的所有子行列式都是正数。
3.若A为n阶正定矩阵，则A为n阶可逆矩阵。

3.5、概率题：抽蓝球红球，蓝结束红放回继续，平均结束游戏抽取次数

3.6、讲一下PCA

参考链接:主成分分析

视频讲解：主成分分析

PCA的思想是将n维特征映射到k维上（k正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

主要优点：有效降维、提取特征

去找到新的坐标系

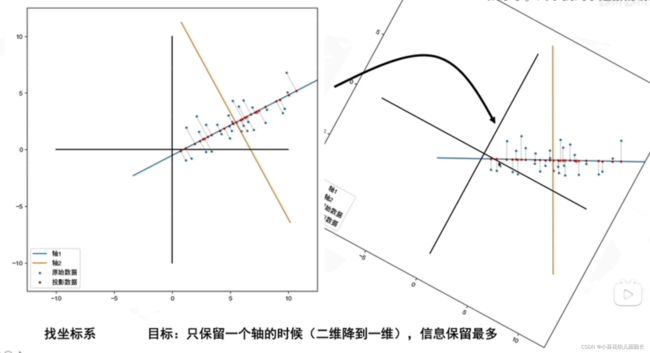
目标：只保留一个轴的时候（二维降到一维），信息保留最多

好的坐标系：找到数据分布最分散的方向（方差最大、更好的保存数据），作为主成分（坐标轴）

PCA步骤：

1. 去中心化（把坐标原点放在数据中心）
2. 找坐标系（找到方差最大的方向）

问题： 怎么找到方差最大的方向？

3.7、拟牛顿法的原理

参考学习:拟牛顿法

求解无约束问题最优化方法的常用方法