第13章 半监督学习

第13章 半监督学习

13.1 未标记样本

有标记样本：样本的类别标记已知

未标记样本：样本的类别标记未知

主动学习的目标是 使用尽量少的查询来获得尽量号的性能

半监督学习(semi-supervised learning)：让学习器不依赖外界交互，自动地利用未标记样本来提升学习性能

聚类假设(cluster assumption)：假设数据存在簇结构，同一簇的样本属于同一类别

流形假设(manifold assumption)：假设数据分布在一个流形结构上，邻近的样本拥有相似的输出值。

纯半监督学习：假定训练数据中的未标记样本并待预测的数据

直推学习：假定学习过程中所考虑的未标记样本恰是待预测数据

13.2 生成式方法

生成式方法(generative methods)是直接基于生成式模型的方法。假设所有数据都是由同一潜在的模型生成的。这个假设通过潜在模型的参数将未标记数据与学习目标联系起来，而未标记数据的标记可看作模型的缺失参数。

给定样本x，其真实类别标记为$y\in \mathcal{Y}$，其中$\mathcal{Y}=\left\{1,2,\dots ,N\right\}$为所有可能的类别，则概率密度生成

$$p\left(x\right)=\sum _{i=1}^N{\alpha }_i\ast p\left(x|{\mu }_i,{\Sigma }_i\right)$$

其中混合系数${\alpha }_i\ge 0,{\sum }_{i=1}^N{\alpha }_i=1;p\left(x|{\mu }_i,{\Sigma }_i\right)$是样本$x$属于第$i$个高斯混合成分的概率；${\mu }_i$和${\Sigma }_i$为该高斯混合成分的参数

令$f\left(x\right)\in \mathcal{Y}$表示模型$f$对$x$的预测标记，$\Theta =\left\{1,2,\dots ,N\right\}$表示样本$x$隶属的高斯混合成分。由最大化后验概率可知

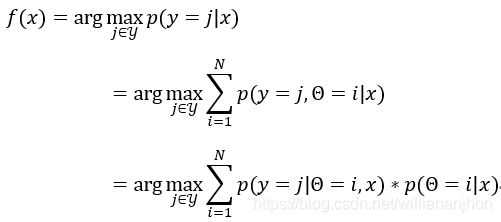
其中

$$p\left(\Theta =i|x\right)=\frac{{\alpha }_i\ast p\left(x|{\mu }_i,{\Sigma }_i\right)}{{\sum }_{i=1}^N{\alpha }_i\ast p\left(x|{\mu }_i,{\Sigma }_i\right)}$$

为样本$x$由第$i$个高斯成分生成的后验概率，$p\left(y=j|\Theta =i,x\right)$为$x$由第$i$个高斯成分生成且其类别为$j$的概率

给定有标记样本集$D_l=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\dots ,\left(x_l,y_l\right)\right\}$和未标记样本集$D_u=\left\{x_{l+1},x_{l+2},\dots ,x_{l+u}\right\},l\ll u,l+u=m$，假设所有样本独立同分布，且都是由同一高斯混合模型生成的。用极大似然法来估计高斯混合模型的参数$\left\{{\alpha }_i,{\mu }_i,{\Sigma }_i|1\le i\le N\right\},D_l\cup D_u$的对数似然为

$$\text{LL}\left(D_l\cup D_u\right)=\sum _{\left(x_j,y_j\right)\in D_l}\ln \left(\sum _{i=1}^N{\alpha }_i\ast p\left(x_j|{\mu }_i,{\Sigma }_i\right)\ast p\left(y_j|\Theta =i,x\right)\right)+\sum _{x_j\in D_u}\ln \left(\sum _{i=1}^N{\alpha }_i\ast p\left(x_j|{\mu }_i,{\Sigma }_i\right)\right)$$

上式由两项组成：基于有标记数据$D_l$的有监督项和基于未标记数据$D_u$的无监督项

高斯混合模型参数估计可用EM算法求解，迭代更新式如下：

E步：根据当前模型参数计算未标记样本$x_j$属于各高斯混合成分的概率

$${\gamma }_{\text{ji}}=\frac{{\alpha }_i\ast p\left(x_j|{\mu }_i,{\Sigma }_i\right)}{{\sum }_{i=1}^N{\alpha }_i\ast p\left(x_j|{\mu }_i,{\Sigma }_i\right)}$$

M步：基于${\gamma }_{\text{ji}}$更新模型参数，其中$l_i$表示第$i$类的有标记样本数目

$${\mu }_i=\frac{1}{{\sum }_{x_j\in D_u}^{}{\gamma }_{\text{ji}}+l_i}\left(\sum _{x_j\in D_u}{\gamma }_{\text{ji}}{x}_j+\sum _{\left(x_j,y_j\right)\in D_l\wedge y_j=i}{x}_j\right)$$

$${\Sigma }_i=\frac{1}{{\sum }_{x_j\in D_u}^{}{\gamma }_{\text{ji}}+l_i}\left(\sum _{x_j\in D_u}{\gamma }_{\text{ji}}\left(x_j-{\mu }_i\right){\left(x_j-{\mu }_i\right)}^T+\sum _{\left(x_j,y_j\right)\in D_l\wedge y_j=i}\left(x_j-{\mu }_i\right){\left(x_j-{\mu }_i\right)}^T\right)$$

$${\alpha }_i=\frac{1}{m}\left(\sum _{x_j\in D_u}{\gamma }_{\text{ji}}+l_i\right)$$

13.3 半监督SVM

半监督支持向量机(Semi-Supervised Support Vector Machine,S3VM)是支持向量机在半监督学习上的推广。

TSVM(Transductive Support Vector Machine)试图考虑对未标记样本进行各种可能的标记指派(label assignment)。

给定$D_l=\left\{\left(x_1,y_1\right),\dots ,\left(x_l,y_l\right)\right\}$和$D_u=\left\{x_{l+1},\dots ,x_{l+u}\right\}$，其中$y_i\in \left\{-1,+1\right\},l\ll u,l+u=m$。TSVM的学校目标是为$D_u$中的样本给出预测标记$\hat{y}=\left\{{\hat{y}}_{l+1},{\hat{y}}_{l+2},..,{\hat{y}}_{l+u}\right\},{\hat{y}}_i\in \left\{-1,+1\right\}$，使得

其中$\left(\omega ,b\right)$确定一个划分超平面；$\xi$为松弛向量，${\xi }_i\left(i=1,2,\dots ,l\right)$对应于有标记样本，${\xi }_i\left(i=l+1,l+2,\dots ,m\right)$对应于未标记样本；$C_l$和$C_u$是由樱花指定的用于平衡模型复杂度、有标记样本与未标记样本重要程度的折中参数

13.4 图半监督学习

给定$D_l=\left\{\left(x_1,y_1\right),\dots ,\left(x_l,y_l\right)\right\}$和$D_u=\left\{x_{l+1},x_{l+2},\dots ,x_{l+u}\right\},l\ll u,$
$l+u=m$，先基于$D_l\cup D_u$构建一个图$G=\left(V,E\right)$，其中结点集$V=\left\{x_1,\dots ,x_l,x_{l+1},\dots ,x_{l+u}\right\}$，边集$E$可表示为一个亲和矩阵(affinity matrix)，长基于高斯函数定义为

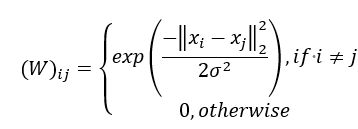
其中$i,j\in \left\{1,2,\dots ,m\right\},\sigma >0$是用户指定的高斯函数带宽参数。

假定从图$G=\left(V,E\right)$将学得一个实值函数$f:V\to \mathbb{R}$，其对于的分类规则为$y_i=\mathrm{sign}\left(f\left(x_i\right)\right),y_i\in \left\{-1.+1\right\}$。关于$f$的能量函数

$$E\left(f\right)=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\left(W\right)}_{\text{ij}}{\left(f\left(x_i\right)-f\left(x_j\right)\right)}^2$$

$$=\frac{1}{2}\left(\sum _{i=1}^m{d}_i{f}^2\left(x_i\right)+\sum _{j=1}^m{d}_j{f}^2\left(x_j\right)-2\sum _{i=1}^m\sum _{j=1}^m{\left(W\right)}_{\text{ij}}f\left(x_i\right)f\left(x_j\right)\right)$$

$$=\sum _{i=1}^m{d}_i{f}^2\left(x_i\right)-\sum _{i=1}^m\sum _{j=1}^m{\left(W\right)}_{\text{ij}}f\left(x_i\right)f\left(x_j\right)={\mathbf{f}}^{\mathbf{T}}\left(\mathbf{D}-\mathbf{W}\right)\mathbf{f}$$

其中$\mathbf{f}=\left({\mathbf{f}}_l^T;{\mathbf{f}}_u^T\right),{\mathbf{f}}_l=\left(f\left(x_1\right),f\left(x_2\right),\dots ,f\left(x_l\right)\right)$，${\mathbf{f}}_u=\left(f\left(x_{l+1}\right),f\left(x_{l+2}\right),\dots ,f\left(x_{l+u}\right)\right)$，分别为$f$在有标记样本和未标记样本上的预测结果，$\mathbf{D}=\text{di}\text{ag}\left(d_1,d_2,\dots ,d_{l+u}\right)$是对角矩阵，其对角元素$d_i={\sum }_{j=1}^{l+u}{\left(W\right)}_{\text{ij}}$为矩阵$\mathbf{W}$的第$i$行元素之和。

具有最小能量的函数$f$在有标记样本上满足$f\left(x_i\right)=y_i\left(i=1,2,..,l\right)$，在未标记样本上满足$△\mathbf{f}=0$，其中$△=\mathbf{D}-\mathbf{W}$为拉普拉斯矩阵(Laplacian matrix)，以第l行于第l列为界，采用分块矩阵表示方法$\mathbf{W}=\left[\begin{array}{cc}{\mathbf{W}}_{\text{ll}}& {\mathbf{W}}_{\text{lu}}\\ {\mathbf{W}}_{\text{ul}}& {\mathbf{W}}_{\text{uu}}\end{array}\right]$，则上式为

$$E\left(f\right)=\left({\mathbf{f}}_l^T;{\mathbf{f}}_u^T\right)\left(\left[\begin{array}{cc}{\mathbf{D}}_{\text{ll}}& {\mathbf{D}}_{\text{lu}}\\ {\mathbf{D}}_{\text{ul}}& {\mathbf{D}}_{\text{uu}}\end{array}\right]-\left[\begin{array}{cc}{\mathbf{W}}_{\text{ll}}& {\mathbf{W}}_{\text{lu}}\\ {\mathbf{W}}_{\text{ul}}& {\mathbf{W}}_{\text{uu}}\end{array}\right]\right)\left[\begin{array}{c}{\mathbf{f}}_l\\ {\mathbf{f}}_u\end{array}\right]$$

$$={\mathbf{f}}_l^T\left({\mathbf{D}}_{\text{ll}}-{\mathbf{W}}_{\text{ll}}\right){\mathbf{f}}_l-2{\mathbf{f}}_u^T{\mathbf{W}}_{\text{ul}}{\mathbf{f}}_l+{\mathbf{f}}_u^T\left({\mathbf{D}}_{\text{uu}}-{\mathbf{W}}_{\text{uu}}\right){\mathbf{f}}_u$$

由$\frac{\partial E\left(f\right)}{\partial {\mathbf{f}}_u}=0$，得

$${\mathbf{f}}_u={\left({\mathbf{D}}_{\text{uu}}-{\mathbf{W}}_{\text{uu}}\right)}^{-1}{\mathbf{W}}_{\text{ul}}{\mathbf{f}}_l$$

令

$$\mathbf{P}={\mathbf{D}}^{-1}\mathbf{W}=\left[\begin{array}{cc}{\mathbf{D}}_{\text{ll}}^{-1}& {\mathbf{D}}_{\text{lu}}\\ {\mathbf{D}}_{\text{ul}}& {\mathbf{D}}_{\text{uu}}^{-1}\end{array}\right]\left[\begin{array}{cc}{\mathbf{W}}_{\text{ll}}& {\mathbf{W}}_{\text{lu}}\\ {\mathbf{W}}_{\text{ul}}& {\mathbf{W}}_{\text{uu}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{D}}_{\text{ll}}^{-1}{\mathbf{W}}_{\text{ll}}& {{\mathbf{D}}_{\text{ll}}^{-1}\mathbf{W}}_{\text{lu}}\\ {\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{ul}}& {\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{uu}}\end{array}\right]$$

即${\mathbf{P}}_{\text{uu}}={\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{uu}},{\mathbf{P}}_{\text{ul}}={\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{ul}}$，则

$${\mathbf{f}}_u={\left({\mathbf{D}}_{\text{uu}}\left(\mathbf{I}-{\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{uu}}\right)\right)}^{-1}{\mathbf{W}}_{\text{ul}}{\mathbf{f}}_l=\left(\mathbf{I}-{\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{uu}}\right){\mathbf{D}}_{\text{uu}}^{-1}{\mathbf{W}}_{\text{ul}}{\mathbf{f}}_l={\left(\mathbf{I}-{\mathbf{P}}_{\text{uu}}\right)}^{-1}{\mathbf{P}}_{\text{ul}}{\mathbf{f}}_l$$

定义一个$\left(l+u\right)\times \left|\mathcal{Y}\right|$的非负标记矩阵$F={\left(F_1^T,F_2^T,\dots ,F_{l+u}^T\right)}^T$，其中第$i$行元素$F_i=\left({\left(F\right)}_{i1},{\left(F\right)}_{i2},\dots ,{\left(F\right)}_{i|\mathcal{Y}|}\right)$为示例$x_i$的标记向量，相应的分类规则为

对$i=1,2,\dots ,m,j=1,2,\dots ,\left|\mathcal{Y}\right|$，将F初始化为

$$F\left(0\right)={\left(Y\right)}_{\text{ij}}=\{\begin{array}{c}1,if\left(1\le i\le l\right)\wedge \left(y_i=j\right)\\ 0,otherwise\end{array}$$

基于W构造一个传播矩阵$S=D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}$，其中$D^{-\frac{1}{2}}=\text{diag}\left(\frac{1}{\sqrt{d_1}},\frac{1}{\sqrt{d_2}},\dots ,\frac{1}{\sqrt{d_{l+u}}}\right)$，有迭代计算式

$$F\left(t+1\right)=\alpha SF\left(t\right)+\left(1-\alpha \right)Y$$

其中$\alpha \in \left(0,1\right)$为用户指定的参数，用于对标记传播$\text{SF}\left(t\right)$与初始化项Y的重要性进行折中，上式迭代至收敛可得


该算法对应于正则化框架

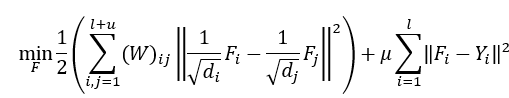
其中$\mu >0$为正则化参数

13.5 基于分歧的方法

基于分歧的方法(disagreement-based methods)使用多学习器，而学习器直接的分歧对未标记数据的利用至关重要。

协同训练正是很好地利用了多视图的相容互补性。

充分：每个视图都包含足以产生最优学习器的信息。

条件独立：在给定类别标记条件下两个视图独立。

13.6 半监督聚类

聚类任务中获得监督信息的类型，第一种类型是必连和勿连约束；第二种类型的监督信息则是少量的有标记样本

约束k均值算法是利用第一类监督信息。给定样本集$D=\left\{x_1,x_2,\dots ,x_m\right\}$以及必连关系集合$\mathcal{M}$和勿连关系集合$\mathcal{C},\left(x_i,x_j\right)\in \mathcal{M}$表示$x_i$和$x_j$必属于同簇，$\left(x_i,x_j\right)\in \mathcal{C}$表示$x_i$和$x_j$必不属于同簇。

给定样本集$D=\left\{x_1,x_2,\dots ,x_m\right\}$，假定少量的有标记样本集为$S={\bigcup }_{j=1}^k{S}_j\subset D$，其中$S_j̸=\varnothing$为隶属第$j$个聚类簇的样本。