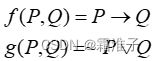【二】头歌平台实验-离散数学逻辑与推理
主要介绍基本逻辑运算,利用逻辑推理解决相关问题。
第1关:命题与逻辑
编程要求:编程得出(P→Q)∧R的真值表的所有结果。
#coding=utf-8
import sympy as sym
# 定义符号p,q,r。
#***** Begin *****#
p =sym.symbols("p")
q =sym.symbols("q")
r =sym.symbols("r")
#***** End *****#
# 输出(p->q)^r。
#***** Begin *****#
sym.pprint(r&(p>>q))
#***** End *****#
# 依次输出 (p->q)^r 的真值表。
#***** Begin *****#
N=[False,True]
print( '{:10} | {:10} | {:10} | {:10}'.format('p','q','r','(p>>q) & r'))
for i in N:
for j in N:
for k in N:
if i==True and j==True and k==False:
pass
else:
print('{:10} | {:10} | {:10} | '.format(str(i),str(j),str(k)),end='')
sym.pprint(((p>>q)&r).subs({p:i, q:j,r: k}))
#***** End *****#
结果显示:
相关知识
1、命题
具有真假意义的陈述句被称为命题。例如,“地球围着太阳转。”(真),“地球围着月亮转。”(假),为了对命题作逻辑演算,我们使用大写字母P,Q,R,...表示命题,称为命题符号。命题的真假我们用0和1表示,真为1,假为0。
2、逻辑联结词
若干个命题可以通过逻辑联结词构成新的命题,称之为复合命题。复合命题的子命题也可以是复合命题,我们称不是复合命题的命题为简单命题,它不包含任何联结词。复合命题的真值依赖于其中的简单命题的真值。有如下五个常用的联结词。
- 否定:设命题
P,与P的真值取值相反的复合命题被称为命题P的否定,记作┐P,读作非P。 - 真值表如下:
使用“sympy”库表示:
import sympy as sym
p = sym.symbols("p")
sym.pprint(~p) # 使用 ~ 符号表示非
sym.pprint((~p).subs({p:True})) # 假设p为真,输出非p的值。结果为:
┐p
False
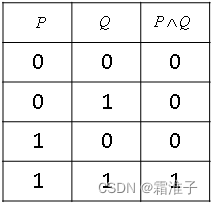
- 合取:设
P,Q是两个命题,复合命题“P并且Q”称为P和Q的合取,记为P∧Q,读作P合取Q,规定P∧Q为真当且仅当P与Q同时为真。真值表如下:
使用“sympy”库表示:
import sympy as sym
p, q = sym.symbols("p q")
sym.pprint(p & q) # 使用 & 符号表示合取
# 假设p真q真,输出p合取q的值。
sym.pprint((p & q).subs({p:True, q:True}))结果为:
p∧q
True
- 析取:设
P,Q是两个命题,复合命题“P或者Q”称为P和Q的析取,记为P∨Q,读作P析取Q,规定P∨Q为真当且仅当P与Q中至少一个为真。真值表如下:
使用“sympy”库表示:
import sympy as sym
p, q = sym.symbols("p q")
sym.pprint(p & q) # 使用 | 符号表示析取
# 假设p真q假,输出p析取q的值。
sym.pprint((p | q).subs({p:True, q:False}))结果为:
p∨q
True
- 蕴含:设
P,Q是两个命题,复合命题“如果P,则Q”称为P蕴含Q,记为P→Q,读作P蕴含Q,称P为条件,Q为结论。规定P→Q为假当且仅当P为真而Q为假。真值表如下:
使用“sympy”库表示:
import sympy as sym
p, q = sym.symbols("p q")
sym.pprint(p >> q) # 使用 >> 符号表示蕴含
# 假设p真q假,输出p蕴含q的值。
sym.pprint((p >> q).subs({p:True, q:False}))结果为:
p→q
False
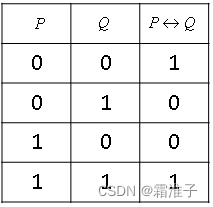
- 等价:设
P,Q是两个命题,复合命题“P当且仅当Q”称为P等价于Q,记为P↔Q,读作P等价于Q,规定P↔Q为真当且仅当P与Q同时为真。真值表如下:
使用“sympy”库表示:
import sympy as sym
p, q = sym.symbols("p q")
# 没有特定的符号表示用析取式表达。
sym.pprint((p >> q) & (q >> p))
# 假设p真q假,输出p等价于q的值。
sym.pprint((p >> q) & (q >> p).subs({p:True, q:False}))结果为:
(p→q)∧(q→p)
False
第2关:命题函数的等价
#coding=utf-8
import sympy as sym
# 定义符号p,q,r。
#***** Begin *****#
p, q, r = sym.symbols("p q r")
#***** End *****#
# 定义命题函数f=(p->q)^(p->r)和 g=p->(q^r)。
#***** Begin *****#
f = sym.Function("f")(p, q , r)
g = sym.Function("g")(p, q, r)
f = (p >> q) & (p >> r)
g = p >> (q & r)
#***** End *****#
# 输出命题函数f,g。
#***** Begin *****#
sym.pprint(f)
sym.pprint(g)
#***** End *****#
# 依次输出两个命题函数的真值表。
#***** Begin *****#
N=[False,True]
for i in N:
for j in N:
for k in N:
print(f.subs({p:i,q:j,r:k}),g.subs({p:i,q:j,r:k}))
#***** End *****#
# 直接判断两个函数是否等价。
#***** Begin *****#
print(f.equals(g))
#***** End *****#相关知识:
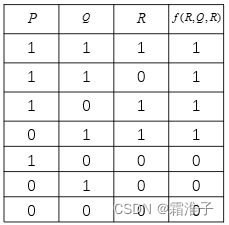
1、命题函数
运用若干个命题以及逻辑联结词进行的组合,我们称为命题公式。例如,P,Q,R均为一个命题,有关它们的函数f(P,Q,R)=(P∧Q)∨R被称为命题函数,我们来看这个命题函数的真值表:
对于四则运算我们有运算的优先级,而对于逻辑联结词我们则有联结词的优先级,五种联结词的运算优先级按如下次序由高到低: 规定括号()内的逻辑运算最先被计算。例如,我们有如下命题公式: 我们可以将其化简为: 使用“sympy"库来创建一个命题函数:
p,q = sym.symbols("p,q")
f = sym.Function("f")(p, q)
f = p >> q2、命题函数的等价
如果命题函数具有相同的真值表,那么它们在逻辑上是等价的。例如我们有如下两个命题函数:
它们的真值表为:
由于真值表相等,两个命题函数在逻辑上也相等。
p,q = sym.symbols("p,q")
f = sym.Function("f")(p, q)
g = sym.Function("f")(p, q)
f = p >> q
g = ~p | q
print(f.subs({p:True,q:True}),g.subs({p:True,q:True}) )输出为:
p→q
q∨┐p
True True
第3关:等值演算
#coding=utf-8
import sympy as sym
# 定义符号p,q。
#***** Begin *****#
p,q=sym.symbols("p,q")
#***** End *****#
# 使用函数验证两个命题公式是否等值,输出结果
#***** Begin *****#
def fun(a, b):
ff = a.subs({p:False,q:False}) == b.subs({p:False,q:False})
ft = a.subs({p:False,q:True}) == b.subs({p:False,q:True})
tf = a.subs({p:True,q:False}) == b.subs({p:True,q:False})
tt = a.subs({p:True,q:True}) == b.subs({p:True,q:True})
if ff and ft and tf and tt:
print(True)
else:
print(False)
f = p&q
g = q&p
fun(f, g)
#***** End *****#
# 将等值演算的每一步命题公式用变量stepx保存,例如step0 = p|~((~q|p)&q)
#***** Begin *****#
step0 = p|~((~q|p)&q)
step1 = p|~(0|(p&q))
step2 = p|~(p&q)
step3 = p|(~p|q)
step4 = (p|~p)|~q
step5 = (1|~q)
#***** End *****#
# 使用函数fun(a,b)验证等值演算每一步。例如,fun(step0, step1)
#***** Begin *****#
fun(step0, step1)
fun(step1, step2)
fun(step2, step3)
fun(step3, step4)
fun(step4, step5)
#***** End *****#相关知识:
1、常用的等值式
我们将一个命题公式的每一组真值(即真值表中的一行)称为该命题公式的一个解释。
设G是一个命题公式,若G在它的所有解释下均为真,则称G为重言式,或称G是永真的。
设G是一个命题公式,若G在它的所有解释下均为假,则称G为矛盾式,或称G是永假的。
设G是一个命题公式,若至少有一个解释使得G为真,则称G为可满足式,或称G是可满足的。
G是永真的,当且仅当非G是永假的,重言式一定是可满足式,反之不然。 若两个命题公式P,Q在其任何解释下,相应的真值均相同,则称P与Q等值,记为P≡Q。
常用的等值式如下:
幂等律:![]()
结合律:![]()
交换律:![]()
分配律:![]()
双重否定律:┐┐p![]() p
p
吸收律:![]()
零律:![]()
同一律:![]()
补余律:![]() ┐p
┐p![]() ┐p
┐p![]()
德摩根律:┐(p![]() )
)![]() ┐p
┐p ![]() ┐q;┐(p
┐q;┐(p![]() q)
q)![]() ┐p
┐p![]() ┐q
┐q
2、等值演算
等值关系是一个等价关系,正是由于这种性质,使得我们可以从某个逻辑公式出发,经过有限次使用常用的等值式,推演出另外一些逻辑公式,这一过程称为等值演算。
例如,证明如下逻辑公式为重言式:
第4关:推理规则
#coding=utf-8
import sympy as sym
# 定义符号p,q。
#***** Begin *****#
p,q=sym.symbols("p,q")
#***** End *****#
# 输出析取三段论,中间逗号使用析取符号。
#***** Begin *****#
sym.pprint((~p & (p |q)) >> q)
#***** End *****#
# 按照例子验证析取三段论为重言式。
#***** Begin *****#
def fun(a):
tt = (a).subs({p:True, q:True})
tf = (a).subs({p:True, q:False})
ft = (a).subs({p:False, q:True})
ff = (a).subs({p:False, q:False})
if tt and tf and ft and ff: # 判断四种解释是否为真
print(True)
else:
print(False)
fun((~p & (p |q)) >> q)
#***** End *****#
# 判断((p -> q) ^ q) -> p 是否为重言式。
#***** Begin *****#
fun(((p >>q)&q)>>p)
#***** End *****#相关知识:
1、推理规则
推理理论:设G和H是两个命题公式,若G→H是重言式,则称H是G的逻辑结果,或称G蕴含H,记为G⇒H。符号⇒是个关系词,而不是逻辑联结词。
由联结词→的定义知,G→H是重言式,当且仅当对G,H的任意解释I,若I满足G,则I也满足H。因此,G⇒H的充要条件是,满足G的解释均满足H。
一些基本的蕴含式:
附加:![]()
化简:![]()
合取:![]()
假言推理:![]()
析取三段论:![]()
拒取式:![]()
假言三段论:![]()
构造性二难:![]()
使用“sympy”库验证附加蕴含式为重言式:
import sympy as sym
p,q = sym.symbols('p q')
sym.pprint(p >> (p | q))
def fun(a):
tt = (p >> (p | q)).subs({p:True, q:True})
tf = (p >> (p | q)).subs({p:True, q:False})
ft = (p >> (p | q)).subs({p:False, q:True})
ff = (p >> (p | q)).subs({p:False, q:False})
if tt and tf and ft and ff: # 判断四种解释是否为真
print(True)
else:
print(False)
fun(p >> (p | q))结果为:
p→(p∨q)
True
可以看到所有解释都为真,输出真,即证为重言式。
-END-![]()