【论文笔记】激光里程计 DMLO: Deep Matching LiDAR Odometry 2020
图森未来
本文提出了基于深度学习方法的激光里程计，首次在激光里程计任务中使用全局稀疏匹配。
其性能超越了现有的DP-based的方法，与几何SOTA方法（SUMA）性能很接近。
相关工作
- 局部迭代方法：ICP系列。应用比较普遍，但是计算量大，异常值敏感，需要很小心的初始化。
- 全局稀疏配准：使用局部几何描述子，大多数手工提取，不适用于稀疏、不均匀的点云数据。
- DP-based：几何不可解释，泛化性不能保证。
本文方法：DMLO
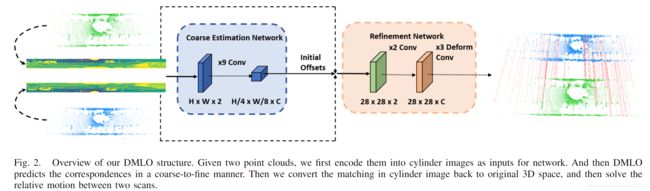
整体流程：
- 首先对输入的前后两个scan点云数据进行柱面投影，投影到2维
- 使用CNN求解匹配对
- 使用NMS＋RANSAC筛选匹配对
- 使用SVD求解相对位姿
1. 柱面投影
点云数据不太好处理：稀疏性，不均匀性，无序性
现有的方法有使用3D卷积、使用pointnet处理等。
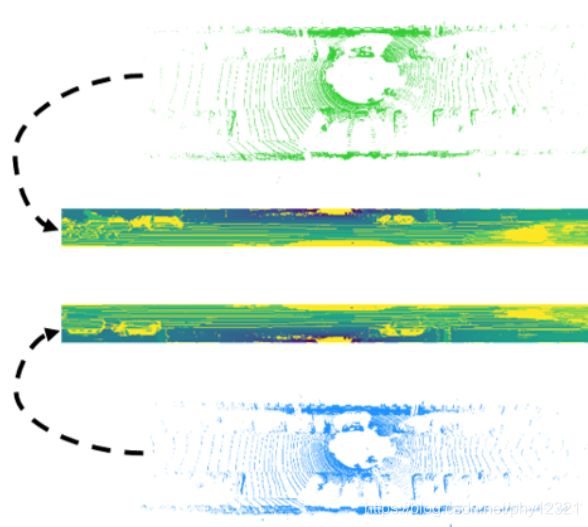
作者选择了柱面投影到二维，得到更为稠密、均匀、紧致的表达。
投影公式：3D->2D,记为函数 Φ ( ) \Phi() Φ()
w = arctan 2 ( y , x ) / Δ θ h = arctan 2 ( z , x 2 + y 2 ) / Δ ϕ \begin{array}{l} w=\arctan 2(y, x) / \Delta \theta \\ h=\arctan 2\left(z, \sqrt{x^{2}+y^{2}}\right) / \Delta \phi \end{array} w=arctan2(y,x)/Δθh=arctan2(z,x2+y2)/Δϕ
2D->3D，记为函数 Φ − 1 ( ) \Phi^{-1}() Φ−1()
z = D ( h , w ) ⋅ sin ( h Δ ϕ ) x = D ( h , w ) ⋅ cos ( h Δ ϕ ) ⋅ cos ( w Δ θ ) y = D ( h , w ) ⋅ cos ( h Δ ϕ ) ⋅ sin ( w Δ θ ) \begin{array}{l} z=\mathbf{D}(h, w) \cdot \sin (h \Delta \phi) \\ x=\mathbf{D}(h, w) \cdot \cos (h \Delta \phi) \cdot \cos (w \Delta \theta) \\ y=\mathbf{D}(h, w) \cdot \cos (h \Delta \phi) \cdot \sin (w \Delta \theta) \end{array} z=D(h,w)⋅sin(hΔϕ)x=D(h,w)⋅cos(hΔϕ)⋅cos(wΔθ)y=D(h,w)⋅cos(hΔϕ)⋅sin(wΔθ)
得到的柱面图像是2通道的，一个记录距离 r = x 2 + y 2 + z 2 r=\sqrt{x^{2}+y^{2}+z^{2}} r=x2+y2+z2，一个记录激光反射强度。
计算label
原始的真值数据只有3D点云之间的转换矩阵，因此需要将每对点云数据根据位姿真值对齐，然后投影到2D柱面, 计算点对之间的匹配关系。
c r = Φ ( p r ) p r ′ = Φ − 1 ( c r ) p t = T p r ′ c t = Φ ( p t ) \begin{array}{l} \boldsymbol{c}_{r}=\Phi\left(\boldsymbol{p}_{r}\right) \\ \boldsymbol{p}_{r}^{\prime}=\Phi^{-1}\left(\boldsymbol{c}_{r}\right) \\ \boldsymbol{p}_{t}=\mathbf{T} \boldsymbol{p}_{r}^{\prime} \\ \boldsymbol{c}_{t}=\Phi\left(\boldsymbol{p}_{t}\right) \end{array} cr=Φ(pr)pr′=Φ−1(cr)pt=Tpr′ct=Φ(pt)
上标 r, t 分别表示 reference 和 target， C，P 表示二维柱面图和三维点云
注意到这里使用 pr’ 而不是 pr 来计算3D空间转换后的target点云坐标pt，因为这种将3D空间坐标投影到2D像素是有量化误差的。直接使用 pr 会引入误差。此外，作者为了减少计算label过程中的量化误差，
-
去除距离过大的噪声点：
e = D t ( c t ) − ∥ p t ∥ 2 e=\mathbf{D}_{t}\left(\boldsymbol{c}_{t}\right)-\left\|\boldsymbol{p}_{t}\right\|_{2} e=Dt(ct)−∥pt∥2
实际上是去掉了入射角较小的点（因为小扰动会导致大误差），这种点距离雷达较远， -
使用子像素损失函数和置信度预测：
假设GT点被投影到二维的坐标为 ( x ˉ i , j , y ˉ i , j ) \left(\bar{x}_{i, j}, \bar{y}_{i, j}\right) (xˉi,j,yˉi,j),其不一定是整数(x,y)。定义概率P：
P i , j ( x , y ) = { ( 1 − Δ x ) ( 1 − Δ y ) Δ x < 1 or Δ y < 1 0 , Δ x ⩾ 1 and Δ y ⩾ 1 \mathbf{P}_{i, j}(x, y)=\left\{\begin{array}{ll} (1-\Delta x)(1-\Delta y) & \Delta x<1 \text { or } \Delta y<1 \\ 0, & \Delta x \geqslant 1 \text { and } \Delta y \geqslant 1 \end{array}\right. Pi,j(x,y)={(1−Δx)(1−Δy)0,Δx<1 or Δy<1Δx⩾1 and Δy⩾1
其中 Δ x = ∣ x ˉ i , j − x ∣ , Δ y = ∣ y ˉ i , j − y ∣ \Delta x=\left|\bar{x}_{i, j}-x\right|, \Delta y=\left|\bar{y}_{i, j}-y\right| Δx=∣xˉi,j−x∣,Δy=∣yˉi,j−y∣.这样就得到了置信度的真值。
根据里程计预测的转换关系计算预测的坐标Q，则可以计算损失函数：
L = − ∑ i , j ∑ x , y P i , j ( x , y ) log ( Q i , j ( x , y ) ) \mathcal{L}=-\sum_{i, j} \sum_{x, y} \mathbf{P}_{i, j}(x, y) \log \left(\mathbf{Q}_{i, j}(x, y)\right) L=−i,j∑x,y∑Pi,j(x,y)log(Qi,j(x,y))
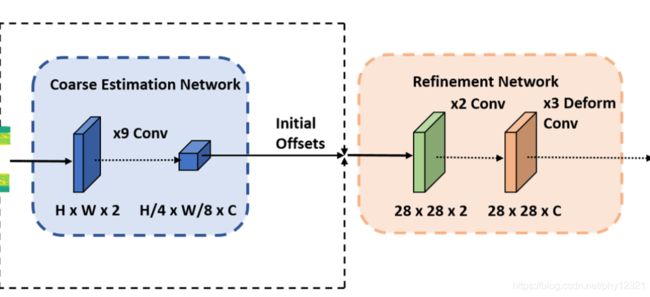
2. CNN求解匹配对
输入是两个柱面图像（HxWx2），预测2D-2D的对应关系，然后转换到3D空间。
作者使用了级联的两个网络进行由粗到细的预测（仿照光流估计，加入了最大位移D），以应对里程计出现的可能的大幅度运动的情况。
两个网络模块的stride不一样（4，8；1，1），D不一样（分别为10和5）此外，第二个refinement network使用了变形卷积以达到自适应感受野的效果，相比于叠加几层网络层更加经济。
根据得到的特征图计算相似性矩阵：
M i , j u , v ( h , w ) = ( x i , j r ) T ⋅ x i + u + h , j + v + w t 其中 h ∈ [ − D − 1 2 , D − 1 2 ] , w ∈ [ − D − 1 2 , D − 1 2 ] \begin{array}{c} \boldsymbol{M}_{i, j}^{u, v}(h, w)=\left(\boldsymbol{x}_{i, j}^{r}\right)^{T} \cdot \boldsymbol{x}_{i+u+h, j+v+w}^{t} \\ \text { 其中 } h \in\left[-\frac{D-1}{2}, \frac{D-1}{2}\right], w \in\left[-\frac{D-1}{2}, \frac{D-1}{2}\right] \end{array} Mi,ju,v(h,w)=(xi,jr)T⋅xi+u+h,j+v+wt 其中 h∈[−2D−1,2D−1],w∈[−2D−1,2D−1]
ij是二维坐标，上标r、t是reference、target，uv是偏移量，hw是stride，D是最大位移。
相当于计算了在reference图像中ij位置的点与在target图像中一块有限区域内L内的每一个点的相似度，然后得到了相似性矩阵。其中L区域表示以ij为中心偏移量为uv，边长为D的区域。
将相似度转化为置信度：
Q i , j u , v ( h , w ) = softmax ( M i , j u , v ( h , w ) ) \mathbf{Q}_{i, j}^{u, v}(h, w)=\operatorname{softmax}\left(\mathbf{M}_{i, j}^{u, v}(h, w)\right) Qi,ju,v(h,w)=softmax(Mi,ju,v(h,w))
3. NMS+RANSAC:
预定义半径R，根据预测的置信度对匹配点对进行非极大值抑制，保留前N个点对。
然后使用RANSAC剔除离群点对。
4. 计算转换关系T
SVD分解。
其他部件：
RANSAC处理后的内点数量少于10时，使用匀速运动模型代替
使用RangeNet++去除运动物体。
实验分析：
与DP方法相比：
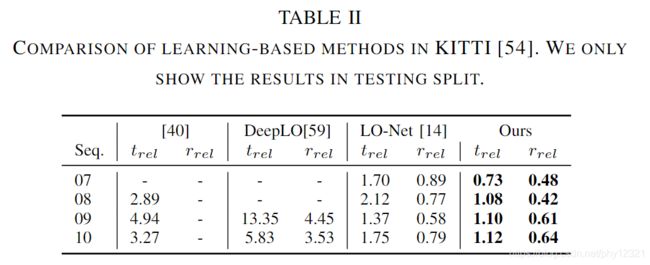
与几何方法相比： 
点云配准性能对比:
未来考虑将RGB信息整合到里程计的框架中。