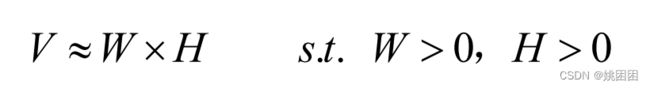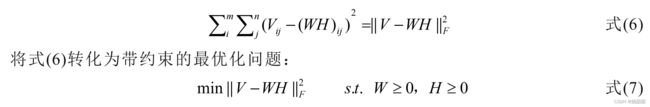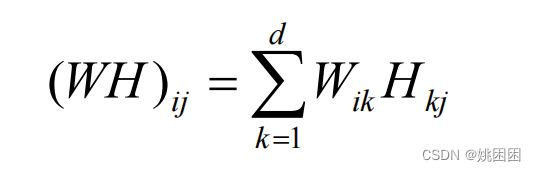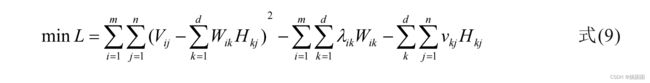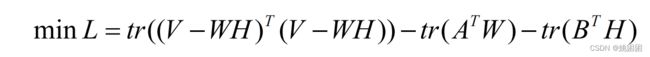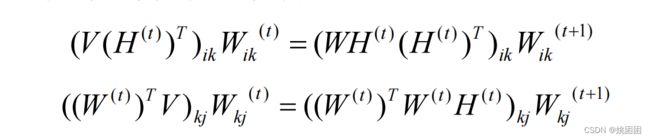期末周总结-矩阵理论-非负矩阵分解

矩阵理论结课作业主要介绍了非负矩阵分解，同时基于非负矩阵分解讲了两个实例。

非负矩阵分解（ Non-negative matrix factorization, NMF ）是一种常用的矩阵分解方法。对于一个 的矩阵 V ，可以将其分解为两个非负矩阵的乘积 W 和 H ( W 和 H 的相乘只能尽量逼近 V ) ，其中 W 的大小为 m d ， H 的大小为 d n 。用数学公式可以将其表示为：

损失函数有多种定义方式，其中最常见的是采用欧氏距离来定义损失函数进而描述 V 和 WH 的近似程度。对于式 (1) ，我们直接想法就是 V 和 WH 每个对应位置的元素都应该尽量接近，所以定义损失函数为

根据矩阵乘法的定义，矩阵WH 的第 i 行 j 列可以表示为

 

结合式 (7) 、式 (8) 和 KKT 条件，我们可以由拉格朗日乘子法得到无约束最优化问题，即：

对于 nn的矩阵 A 和 B，我们有以下表示：

 对上式子进行整理可以得到：

 对其进行矩阵求导并整理可以得到

 上述式子可以通过迭代法来求解

关于NMF的应用

第一个使用 NMF 做推荐算法（在CSDN上看一个大佬写的，自己修改了以下）

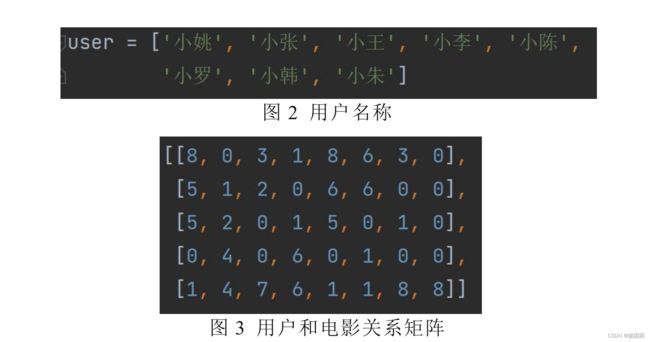
该算法首先定义用户和电影两个集合，通过每个用户对部分电影的打分，预测该用户对其他没看过电影的打分值，这样可以根据打分值为该用户做出推荐。其中，用户和电影的关系，可以用一个矩阵来表示，每一列表示用户，每一行表示电影，每个元素的值表示用户对已经看过的电影的打分。

接下来，我们预先设置这些电影可以分为两个部分，然后使用库函数对电影

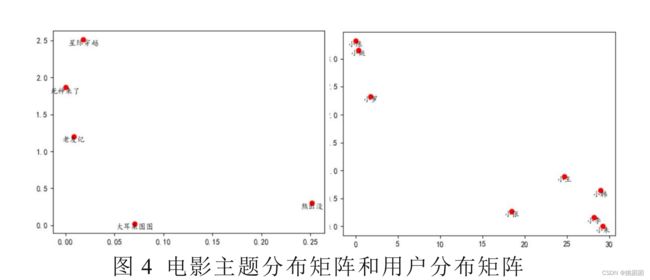
主题分布矩阵和用户分布矩阵进行绘制

 

如上图 所示，在设置电影主题数为 2 的情况下， “ 星际穿越 ” ， “ 死神来了 ” ， “ 老友记” 三者更加接近，而 “ 大耳朵图图 ” 和 “ 熊出没 ” 更加接近。通过分析后两者属于动画片，因此我认为这种分法是较为合理的。在用户分布矩阵中，“ 小姚 ” 和 “ 小陈 ” 极度相似，这两个用户仅在“ 死神来了 ” 这个影片上评分不同，其余评分都是相同的，因此我们认为这一划分也是合理的。最后，我们对该算法进行测试，选择用户“ 小姚 ”让算法为其推荐影片， 由下图 可以看出，因为 “ 小姚 ” 没有对 “ 大耳朵图图 ” 有过评分，因此算法会将该影片推荐给用户。

到此为止，使用 NMF 做推荐算法的整个过程已经完整呈现。但根据上文对矩 阵分解概念的介绍，我们知道在矩阵分解中一定会有误差。在这个案例中，误差主要来源于预先设置的电影主题数目，接下来本文设置不同的电影主题数目并记录误差（如下表 所示）。由表可知，随着主题的增多误差逐渐降低。原因在于主题越多，越接近原始矩阵，所以误差越少。

 这也启示我们在使用 NMF 做推荐算法时，要提前确定好需求再定义聚类数目

第二个使用 NMF 识别手写体

由上述对 NMF 的简单介绍可以知道， NMF 主要是对原始矩阵进行分解以得特征矩阵 W 和系数矩阵和 H ，这启发我们可以利用 NMF 实现特征提取。本节选取了著名的手写体数据集—2-digits ，对其使用 NMF 实现特征提取。图 6 是该数据集真实分布，由图可知，该数据集由 64 张照片组成，其中每张照片中含有两个数字。

 对于该数据集的处理本文采用的主要步骤如下：

1 、随机初始化特征矩阵 W 和系数矩阵和 H ，设定特征提取数目、误差阈值和

迭代次数

2 、基于前文所介绍的求解方法对 W 和 H 进行迭代更新

3 、当误差小于误差阈值或达到迭代次数，更新停止

4 、输出特征矩阵 W ， W 矩阵的每一列即为一个特征（对应一个数字）

5 、将得到的 W 矩阵进行绘制，得到识别结果

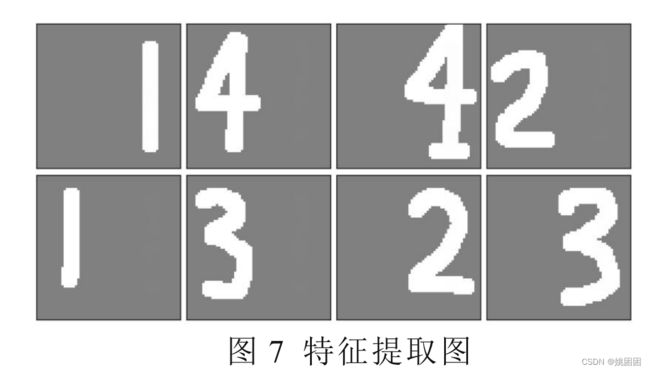
下图利用 NMF 识别后的结果，如果所示 NMF  的较为清晰地识别出 8 个特征数目（8 是预先在程序中设置的特征提取数目）。

总结

在大数据时代，数据大多呈现出维数高，数据量大等特点。缩减数据维数是指从高维数据中提取知识，发现内在规律，减少冗余，增强特征价值密度，进而提高后续计算效率。非负矩阵分解作为非线性且带有非负约束的矩阵分解降维方法，具有可解释性强、计算方便、可大规模处理数据等优点。