多目标启发式算法(NSGA2, MOEA, MOPSO)python实现

1. MODA-多目标差分进化算法

基于快速非支配排序算法和拥挤度。

算法主程序

def MODE(nIter, nChr, nPop, F, Cr, func, lb, rb):
    """多目标差分进化算法主程序 
    Params:
        nIter: 迭代次数
        nPop: 种群规模 
        F: 缩放因子 
        Cr: 交叉概率 
        func：优化函数 
        lb: 自变量下界 
        rb：自变量上界 
    Return：
        paretoPops: 帕累托解集 
        paretoFits: 对应的适应度 
    """
    # 生成初始种群 
    parPops = initPop(nChr, nPop, lb, rb) 
    parFits = fitness(parPops, func) 

    # 开始迭代  
    iter = 1 
    while iter <= nIter:
        # 进度条 
        print("【进度】【{0:20s}】【正在进行{1}代...】【共{2}代】".\
            format('▋'*int(iter/nIter*20), iter, nIter), end='\r')

        mutantPops = mutate(parPops, F, lb, rb)  # 产生变异向量 
        trialPops = crossover(parPops, mutantPops, Cr)  # 产生实验向量 
        trialFits = fitness(trialPops, func)  # 重新计算适应度 

        pops = np.concatenate((parPops, trialPops), axis=0)  # 合并成新的种群
        fits = np.concatenate((parFits, trialFits), axis=0) 
        ranks = nonDominationSort(pops, fits)  # 非支配排序 
        distances = crowdingDistanceSort(pops, fits, ranks)  # 计算拥挤度 

        parPops, parFits = select1(nPop, pops, fits, ranks, distances)   

        iter += 1 
    print("\n") 
    # 获取等级为0，即实际求解得到的帕累托前沿 
    paretoPops = pops[ranks==0] 
    paretoFits = fits[ranks==0] 
    
    return paretoPops, paretoFits

由父代种群和经过差分变异交叉后的实验种群混合成一个新的种群，对新的种群进行非支配排序，利用1对1锦标赛选择算子筛选出新的父代种群。

2. NSGA2-非支配排序遗传算法

采用精英策略，在进行交叉变异操作之后对新产生的种群与父代种群混合成新的种群，对新的种群进行优选。

算法主程序

def NSGA2(nIter, nChr, nPop, pc, pm, etaC, etaM, func, lb, rb): 
    """非支配遗传算法主程序 
    Params:
        nIter: 迭代次数 
        nPop: 种群大小 
        pc: 交叉概率 
        pm: 变异概率 
        func: 优化的函数 
        lb: 自变量下界
        rb: 自变量上界
     Return：
        paretoPops: 帕累托解集 
        paretoFits: 对应的适应度  
    """   
    # 生成初始种群 
    pops = initPops(nPop, nChr, lb, rb)  
    fits = fitness(pops, func) 

    # 开始第1次迭代 
    iter = 1 
    while iter <= nIter:
        print(f"当前正在第{iter}代....")
        ranks = nonDominationSort(pops, fits)  # 非支配排序 
        distances = crowdingDistanceSort(pops, fits, ranks)  # 拥挤度
        pops, fits = select1(nPop, pops, fits, ranks, distances) 
        chrpops = crossover(pops, pc, etaC, lb, rb)  # 交叉产生子种群 
        chrpops = mutate(chrpops, pm, etaM, lb, rb)  # 变异产生子种群 
        chrfits = fitness(chrpops, func)  
        # 从原始种群和子种群中筛选 
        pops, fits = optSelect(pops, fits, chrpops, chrfits)  
        iter += 1 
    # 对最后一代进行非支配排序 
    ranks = nonDominationSort(pops, fits)  # 非支配排序 
    distances = crowdingDistanceSort(pops, fits, ranks)  # 拥挤度 
    paretoPops = pops[ranks==0] 
    paretoFits = fits[ranks==0] 
    return paretoPops, paretoFits 

3. MOPSO-多目标粒子群算法

从archive集中更新gBest不仅采用支配解，还利用网格法，统计支配解的密度，选取网格中密度较低的解来更新gBest。

算法主程序

def MOPSO(nIter, nPop, nAr, nChr, func, c1, c2, lb, rb, Vmax, Vmin, M):
    """多目标粒子群算法
    Params:
        nIter: 迭代次数 
        nPOp: 粒子群规模 
        nAr: archive集合的最大规模 
        nChr: 粒子大小 
        func: 优化的函数
        c1、c2: 速度更新参数 
        lb: 解下界
        rb：解上界 
        Vmax: 速度最大值 
        Vmin：速度最小值 
        M: 划分的栅格的个数为M*M个
    Return:
        paretoPops: 帕累托解集
        paretoPops：对应的适应度 
    """
    # 种群初始化 
    pops, VPops = initPops(nPop, nChr, lb, rb, Vmax, Vmin) 
    # 获取个体极值和种群极值 
    fits = fitness(pops, func) 
    pBest = pops 
    pFits = fits 
    gBest = pops
    # 初始化archive集, 选取pops的帕累托面即可
    archive, arFits = getNonDominationPops(pops, fits) 
    wStart = 0.9 
    wEnd = 0.4  

    # 开始主循环 
    iter = 1 
    while iter <= nIter:
        print("【进度】【{0:20s}】【正在进行{1}代...】【共{2}代】".\
            format('▋'*int(iter/nIter*20), iter, nIter), end='\r') 

        # 速度更新 
        w = wStart - (wStart-wEnd) * (iter/nIter)**2 
        VPops = w*VPops + c1*np.random.rand()*(pBest-pops) + \
            c2*np.random.rand()*(gBest-pops) 
        VPops[VPops>Vmax] = Vmax 
        VPops[VPops<Vmin] = Vmin 
        # 坐标更新 
        pops += VPops 
        pops[pops<lb] = lb 
        pops[pops>rb] = rb  # 防止过界 
        fits = fitness(pops, func) 

        # 更新个体极值 
        pBest, pFits = updatePBest(pBest, pFits, pops, fits) 
        # 更新archive集 
        archive, arFits = updateArchive(pops, fits, archive, arFits) 
        # 检查是否超出规模，如果是，那么剔除掉一些个体 
        archive, arFits = checkArchive(archive, arFits, nAr, M)  
        # 重新获取全局最优解
        gBest = getGBest(pops, fits, archive, arFits, M)  
        iter += 1 
    print('\n')
    paretoPops, paretoFits = getNonDominationPops(archive, arFits) 
    return paretoPops, paretoFits 

4. 测试算例

FON标准问题：
$$f_1(x_1,x_2,x_3)=1-e^{-{\sum }_{i=1}^3(x_i-\frac{1}{\sqrt{3}})},f_2(x_1,x_2,x_3)=1-e^{-{\sum }_{i=1}^3(x_i+\frac{1}{\sqrt{3}})}$$
其中：$x_i\in [-2,2],i=1,2,3$

该问题具有极为简单易于表达的理论最优解集
$$x_1=x_2=x_3\in [-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}]$$

4. 测试结果

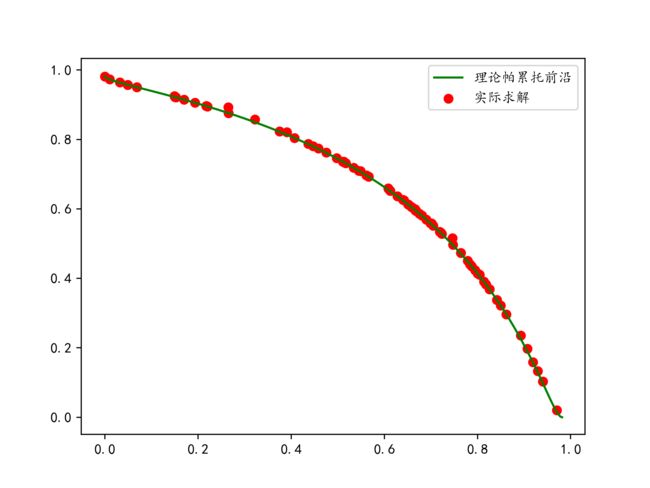
4.1. 多目标差分进化算法求解结果

（迭代次数100，种群规模50）

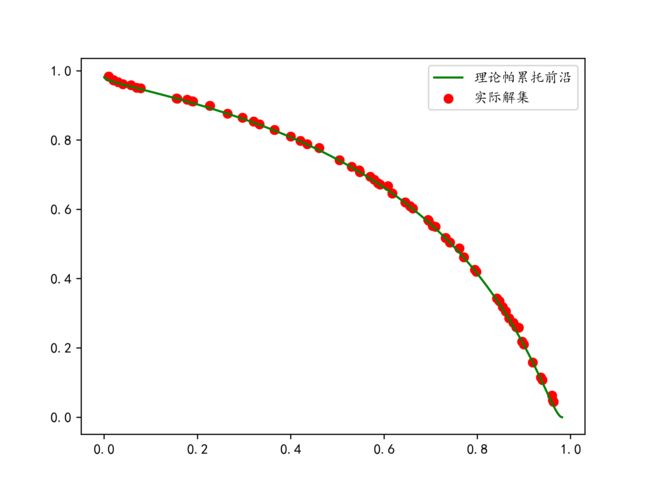
4.2. NSGA2算法求解结果

（迭代次数50，种群规模100）

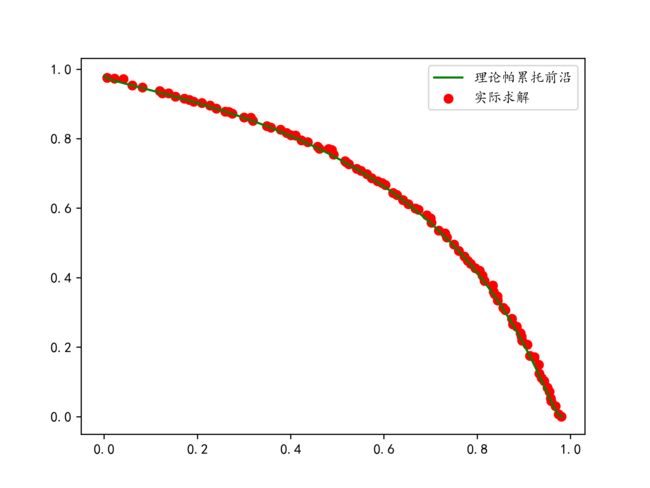
4.3 MOPSO算法求解结果

（迭代次数100，种群规模100）

4.4 结果对比

• 求解速度：MOPSO > MODA > NSGA2
• 求解质量：MOPSO > NSGA2 > MODA

---

5. 参考文献

参考文献：多目标差分进化在热连轧负荷分配中的应用
参考博客：多目标优化算法（一）NSGA-Ⅱ（NSGA2)
参考文献：MOPSO算法及其在水库优化调度中的应用
详细代码地址：部分多目标启发式算法python实现(github)