【网络流】 Ford-fulkerson算法__Dinic算法

适合初学者看的网络流知识点大全

---

网络流是什么

网络流是图论中一个非常重要的板块，也非常实用，经常在设计巴士路线，连接网线和运输水都有广泛运用，那为什么这样说呢，我们先来看一个例子

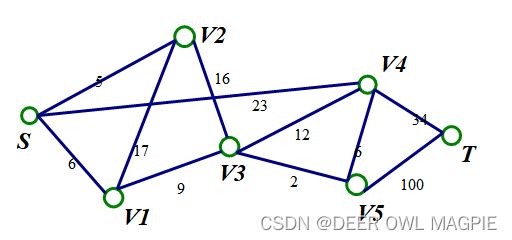
在生活中，我们常常会遇到这样一类问题，我们要把水从S点运送到T点，其中有很多条道路，我们要经过不同的点最终到达T点，而每条道路都有一个他自己的最大容量，也就是说把水从这条管道运送时运送的数量不能超过他的容量，在这个基础上让我们求各种最值问题，因为这些管道像网络一样密密麻麻的分布着，所以我们又把这类问题称为网络流。

网络流

网络流是一个很复杂的专题，刚接触网络流动朋友一定会出现这个问题：网络流的情况那么多，一会儿最大流，一会儿最小割，一会儿又有费用，咋那么多呢。这个时候我们就需要来梳理一下网络流的基本结构了，也就是他到底分为哪几个板块，然后系统的去学习。在学习的过程中，你会发现，网络流的算法一般都是特别复杂的，你刚学的时候会搞不清步骤，会感觉很复杂，这时候，小编推荐大家多看几遍相关文章或视频，多学习几遍，相信你的记忆和理解就会更深一层。

一般来说，网络流大概分为以下几个板块：
1.无权问题：这是最简单的问题。
2.纯最大流：这种问题和后面的问题都是加权问，相对来说复杂
3.最小割最大流问题
4.最小费用最大流问题，这一类问题给每条边多加了一个权值，下文会讲解。

PS:这篇文章中我们重点讲解用福德福克森解决第一类问题，其他问题参见后续博文。
我们会发现，网络流就是一个为人民服务的知识，他的问题无论是难还是简单都接近实际，如费用问题，所以网络流在生活和基建上（包括数学建模）都得到广泛运用。

无权流

我们先来看看无权问题，这类问题主要是求在一幅图中，最多存在有多少条合法的且互不相交的流。这个问题很基础，他的关键在于互不相交，这里的不相交指的是没有重复的边，但允许有重复的点。但我们一定要理解透彻它的概念，后面学起来就不难了。
来看一个图，我们忽略到线段的权值

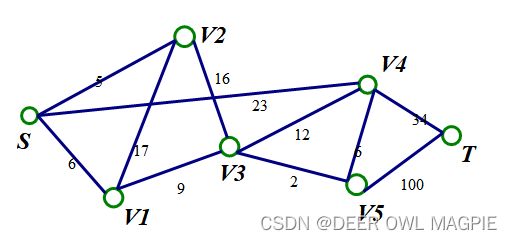
我们说，最大流就是指从S点出发到T点的最大流量，这个流量就是指能运输多少水到T点（除源点和汇点外任意一点不接收水也不放水），也就是说中转点有多少水流过来，就要放多少水流走。我们在学习之前先来看几个相关概念以便理解：

1.源点：顾名思义，出发点，也就是图中的S点。
2.汇点：就是最后需要到达的重点，如图中T点。
3.容量：每条路径最大限度。

还有一些概念我们会在之后的讲解中陆续提到。

Ford-Fulkerson算法

接下来，我们要介绍两种解决无权问题的算法。第一种是此类算法的经典。
福德-福克森算法是由福德和福克森在1956年提出了，其基于贪心思想运用dfs或bfs来实现（当然这个算法可以解决很多类问题）他主要的操作在于纠正错误，那么这个算法到底会犯下什么样的错误呢。

算法思路

首先我们来了解一个割的概念：
割把一个图分为两个集合，保证S集合包含源点，T集合包含汇点，要求将这条割所在的所有线段割断后，没有道路可以从S集合里的任意一点直接连通T集合内的任意一点（只说的是S不能到达T，但T可以以反向边的方式到达S）。割断了几条线段就是这个割的大小。
还有一个定理：
在流不相交的前提下，无权问题的不相交流量数量一定是等于最小割的，还小于等于任意一条割因为每一条流都会从S集合去到T集合，此时从S集合到T集合一共只有最小割条边，若保证互不相交，那么流量数一定小于最小割。

通俗来讲，整个算法大致分为以下步骤：
1.用dfs随意找到一条流。
2.和最优解作比较，删掉多余边并标记剩余边。
3.一直这样循环，直至找不到合法流，dfs将返回一个大小为0的割

我们来举个例子：

假设有一个图是这样的（都是有向图哦）

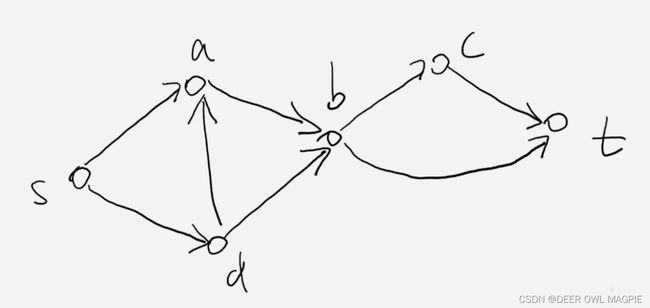
我们的目的是要得到在互不相交的情况下最多有多少条合法边。
都说贪心容易出错，那么他到底会犯下什么错误呢

这是最优解

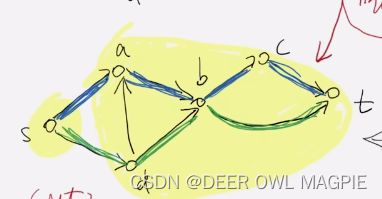
这里我们发现这个图的最小割是二，而不相交的流量数也是二，从而证实了上文的定理。
回到正题，贪心算法会做出什么样的错误呢，如图

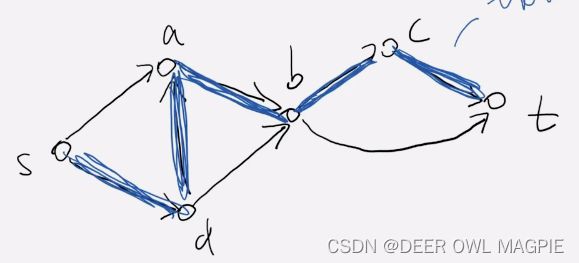
如果你的贪心算法运气不巧，那么你就会得到这样一条阻塞流。

阻塞流：顾名思义，这条流会堵住所有流去汇点的通道，我们越晚得到阻塞流越好。

当我们得到阻塞流时，就意味着算法该结束了，但这并不是最优解，所以我们要进行纠错：

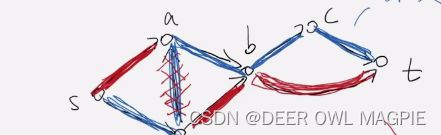
如图，和我们刚才说的步骤一样，将多余的边，也就是竖着的那条删掉，将缺少的边补上，我们的算法就已经大致成型。
换句话说，其实这个操作就是将多余的反向连接，差的边补上，如此循环就可以得到最终结果了，最后的图是这样的：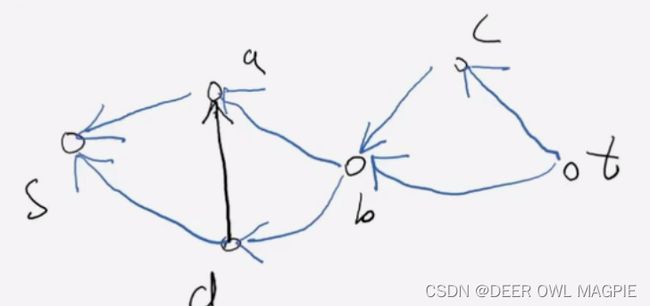

我们知道这个例子一共经过两次操作就得到了最后的图，应该还是相对简单的。当我们得到这个图时，我们可以找到最小割，其大小一定为0。
但是我们知道，有些边我们在算法运作的过程中是改变了他的方向的，那么我们现在要将这个割还原回去，也就是将方向全部转回来，如这个例子，将所有转换了方向的边转回来后，我们发现我们得到的最小割其实大小为二，这时候我们可以说原图最小割大小为二，找到最小割后，自然也得出了不相交的最大流，他的数量也就是最小割，福德福克森算法将最小割=最大流这个定理巧妙且不突兀的运用进了这类问题。
到这个时候，算法就圆满结束了。

算法展望

相信大家刚刚看到这个问题时，会不由得想到动态规划吧，这也是一种好方法，这里就不介绍了。而福德福克森算法的思想与DP完全不同，虽然用了较为暴力的贪心算法，但大致的思路却不是硬着头皮去枚举，而是巧妙地运用了最小割=最大流定理，通过寻找最小割来间接求得最大流，这种转换的思想是很常用的，也值得我们深入学习。

最大流

最大流是我们网络流算法的第二类问题，它主要是用来解决水管运输时找到流量最值，在最大流算法的领域中，ford-fulkerson同样适用，但是在1970年，一个名为dinitz的人发明了一种全新的算法，当时发表在苏联，由于排版原因未能讲的非常详细，刚开始西方人民并不知道这个算法，直到1986年，以色列两名学者发现了这个算法，在研究很久后，发表在西方刊目上，才被人民所熟知，，但是有趣的是，这两名以色列学者拼写错了dinitz的名字，写成了dinic，从此，这个算法也叫dinic算法。下面我们就来讲解一下这个算法。

Dinic算法

这个算法采用分层思想，也就是把所有顶点分为几层，当你听到的时候，相信你会不由自主的想到状态转移，但dinic算法的核心思想不仅仅是状态转移，而是构建一个level graph 话不多说，我们直接来看一个例子：
有下图：

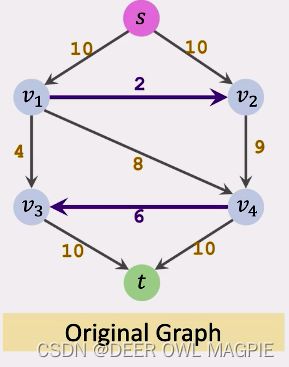
第一步：构建level graph

1.分层：
一层一层的分，但是这个分层并不是眼睛看那些点在一行，而是以线为标准，若S点走一步能到达的点叫第一层，走两步能到达且不在第一层内的点叫做第二层，走三步能到达且不在第一层或第二层内的点记做第三层。换句话说：S点一步能走到的点记做第一层，第一层的点一步能走到的的所有点都记做第二层，第二层的点一步能走到的点且不在第一层内的点叫做第三层，以此类推，S点和T点单独分为一层。

2.删线：
再分层分好以后，我们要删除一些线，具体要删哪些线，首先我们先拿到手上的level graph若两点在不同层中，且在原图中有线连接，那么这两点就连接起来，若无线连接，就不连；若两点在同一层中，不管有没有线连接，都不连。总的来说就是在原图的基础上删掉连接同层两点的线。

就如上面的例子，我们最终得到了一棵level graph，如图：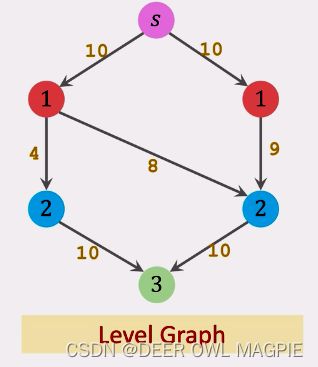
这棵level graph树删除了上图两条连接同一层中点的边，也就是两条紫色的边，此图用数字标出了层次。

第二步：构建residual graph

接下来进入第二步，构建：residual graph，也就是，体现出水管的空闲量。刚开始时，residual graph就是原图，因为水管都是空闲的。
示意图：

Created with Raphaël 2.3.0 开始 将residual graph 转换成新的 level graph， 再寻找level graph的阻塞流 找到阻塞流后 更新residual grap h的空闲量， 随后用总流量-空闲量 得到新的总流量 去掉总流量为0的边 再给这些边添加反向边， 每一条边都需要添加 反向边，找到的阻塞流 值为多少就添加值为 多少的反向边，如果为零 则不用添加。若遇到平行边 ，就合并这些边 结束 yes no

这样的过程一直循环下去直到图中只剩一条链，这时，我们把residual graph中的反向边全部删掉，再拿出原图，我们拿原图减去residual graph 每天边对应相减权值，得到最终的图，最后原图中与S相接的边权值之和就是最大流了。算法结束了。

算法展望

这个算法是基于分层思想，由于没有那么多的纠错过程，其时间复杂度远远高于Ford-fulkerson算法（这里仅仅指解决最大流问题时的ford-fulkerson算法），所以这个算法也被广泛采纳。dinic算法每次更新level graph和residual graph，这个更新的过程与动态规划极其相似，也可以说，其中蕴含着DP思想。