哈夫曼编码（1）哈夫曼编码的基本概念及应用【c++】和哈夫曼树算法的基本思想

​
哈夫曼编码这个词相信大家都不陌生，它是一种给字符编码的工具，发明他的人是美国的哈夫曼大叔，这个编码是用来压缩文件的，他要满足的是：

1.每个字符的编码中只含数字0,1；

2.每一个字符的编码都不是另一个字符的前缀（这样才保证输入的编码无歧义）

3.尽可能保证数量少（公式：每一个字符的频率*编码长度之和）

为了更好地满足这三个条件，我们创造出了一个以树和集合为基础的算法，就叫哈夫曼算法；

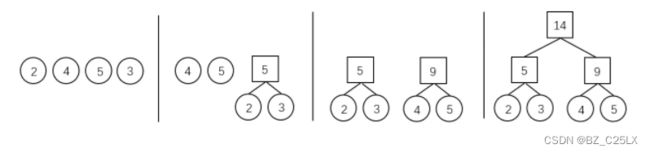
哈夫曼算法先是定义多个子树，有多少个字符就定义多少个树，这些树刚开始时都存于一个集合中，每一步把当前森林中频率最小的两棵子树合并为一棵子树 ，原始树作为子节点或子树，他的父亲的权值就是两个子节点的权值和，这可子树只能是二叉树，这一棵新树也存放与集合中，并代替掉了刚刚的两棵子树，这棵新树的频率就是那两棵子树的频率和…以此类推，重复操作。最后得到的树一定满足每个非叶节点恰好有两个子节点（因为编码只有0和1).

下面是此树的构造过程

注意：每两个子树合并为一个时，一定要添加父节点，不能直接将其中一个子树作为其父节点。

构造出树后，我们把每一条边都标上数值，保证每一个非叶节点的两个儿子的边有一个是0.有一个是1，这样才不会出现重复。

哈夫曼编码的计算过程：

刚才说了，我们要尽可能让哈夫曼编码的值小，这也是为什么要用最小的权值子树作为子树，这样可以让深度越深的字符权值越小，那么，哈夫曼编码的计算过程为：每个字符权值*长度之和。

应用：

[NOI2015] 荷马史诗

题目背景

追逐影子的人，自己就是影子 —— 荷马

题目描述

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有 $n$ 种不同的单词，从 $1$ 到 $n$ 进行编号。其中第 $i$ 种单词出现的总次数为 $w_i$。Allison 想要用 $k$ 进制串 $s_i$ 来替换第 $i$ 种单词，使得其满足如下要求：

对于任意的 $1\le i,j\le n$ ，$i\ne j$ ，都有：$s_i$ 不是 $s_j$ 的前缀。

现在 Allison 想要知道，如何选择 $s_i$，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的 $s_i$ 的最短长度是多少？

一个字符串被称为 $k$ 进制字符串，当且仅当它的每个字符是 $0$ 到 $k-1$ 之间（包括 $0$ 和 $k-1$ ）的整数。

字符串 $str1$ 被称为字符串 $str2$ 的前缀，当且仅当：存在 $1\le t\le m$ ，使得 $str1=str2[1..t]$。其中，$m$ 是字符串 $str2$ 的长度，$str2[1..t]$ 表示 $str2$ 的前 $t$ 个字符组成的字符串。

输入格式

输入的第 $1$ 行包含 $2$ 个正整数 $n,k$ ，中间用单个空格隔开，表示共有 $n$ 种单词，需要使用 $k$ 进制字符串进行替换。

接下来 $n$ 行，第 $i+1$ 行包含 $1$ 个非负整数 $w_i$，表示第 $i$ 种单词的出现次数。

输出格式

输出包括 $2$ 行。

第 $1$ 行输出 $1$ 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 $2$ 行输出 $1$ 个整数，为保证最短总长度的情况下，最长字符串 $s_i$ 的最短长度。

样例 #1

样例输入 #1

4 2
1
1
2
2

样例输出 #1

12
2

样例 #2

样例输入 #2

6 3
1
1
3
3
9
9

样例输出 #2

36
3

提示

【样例解释】

样例 1 解释

用 $X(k)$ 表示 $X$ 是以 $k$ 进制表示的字符串。

一种最优方案：令 $00(2)$ 替换第 $1$ 种单词， $01(2)$ 替换第 2 种单词， $10(2)$ 替换第 $3$ 种单词，$11(2)$ 替换第 $4$ 种单词。在这种方案下，编码以后的最短长度为：

$1\times 2+1\times 2+2\times 2+2\times 2=12$

最长字符串 $s_i$ 的长度为 $2$ 。

一种非最优方案：令 $000(2)$ 替换第 $1$ 种单词，$001(2)$ 替换第 $2$ 种单词，$01(2)$ 替换第 $3$ 种单词，$1(2)$ 替换第 $4$ 种单词。在这种方案下，编码以后的最短长度为：

$1\times 3+1\times 3+2\times 2+2\times 1=12$

最长字符串 $s_i$ 的长度为 $3$ 。与最优方案相比，文章的长度相同，但是最长字符串的长度更长一些。

样例 2 解释

一种最优方案：令 $000(3)$ 替换第 $1$ 种单词，$001(3)$ 替换第 $2$ 种单词，$01(3)$ 替换第 $3$ 种单词， $02(3)$ 替换第 $4$ 种单词， $1(3)$ 替换第 5 种单词， $2(3)$ 替换第 $6$ 种单词。

【数据规模与约定】

所有测试数据的范围和特点如下表所示（所有数据均满足 $0<w_i\le 10^{11}$）：

测试点编号	$n$ 的规模	$k$ 的规模	备注
$1$	$n=3$	$k=2$
$2$	$n=5$	$k=2$
$3$	$n=16$	$k=2$	所有 $w_i$ 均相等
$4$	$n=1000$	$k=2$	$w_i$ 在取值范围内均匀随机
$5$	$n=1000$	$k=2$
$6$	$n=100000$	$k=2$
$7$	$n=100000$	$k=2$	所有 $w_i$ 均相等
$8$	$n=100000$	$k=2$
$9$	$n=7$	$k=3$
$10$	$n=16$	$k=3$	所有 $w_i$ 均相等
$11$	$n=1001$	$k=3$	所有 $w_i$ 均相等
$12$	$n=99999$	$k=4$	所有 $w_i$ 均相等
$13$	$n=100000$	$k=4$
$14$	$n=100000$	$k=4$
$15$	$n=1000$	$k=5$
$16$	$n=100000$	$k=7$	$w_i$ 在取值范围内均匀随机
$17$	$n=100000$	$k=7$
$18$	$n=100000$	$k=8$	$w_i$ 在取值范围内均匀随机
$19$	$n=100000$	$k=9$
$20$	$n=100000$	$k=9$

【提示】

选手请注意使用 64 位整数进行输入输出、存储和计算。

【评分方式】

对于每个测试点：

• 若输出文件的第 $1$ 行正确，得到该测试点 $40\%$ 的分数；
• 若输出文件完全正确，得到该测试点 $100\%$ 的分数。

​分析：本题所构造的编码其实就是huffman编码，我们可以把单词的次数作为哈夫曼树叶子节点的权值，求出k叉哈夫曼树就行了。 答案就为所有叶子节点的wpl，最深叶子节点的深度了
代码：

#include
#include
#include
#include
#define ll long long
using namespace std;
struct node
{
    ll w,h;
    node(){w=0,h=0;}
    node(ll w,ll h):w(w),h(h){}
    bool operator <(const node &a)const{return a.w==w?h>a.h:w>a.w;}
};
ll ans;
priority_queue<node>q;
int main()
{
    ll n,k;ans=0;scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;i++)
    {
        ll w;scanf("%lld",&w);
        q.push(node(w,1));
    }
    while((q.size()-1)%(k-1)!=0)q.push(node(0,1));
    while(q.size()>=k)
    {
        ll h=-1;ll w=0;
        for(int i=1;i<=k;++i)
        {
            node t=q.top();q.pop();
            h=max(h,t.h);
            w+=t.w;
        }
        ans+=w;
        q.push(node(w,h+1));
    }
    printf("%lld\n%lld\n",ans,q.top().h-1);
    return 0;
}

持续更新，感谢支持！