作业5:SVM实现鸢尾花分类
作业5:SVM实现鸢尾花分类
1. SVM 介绍
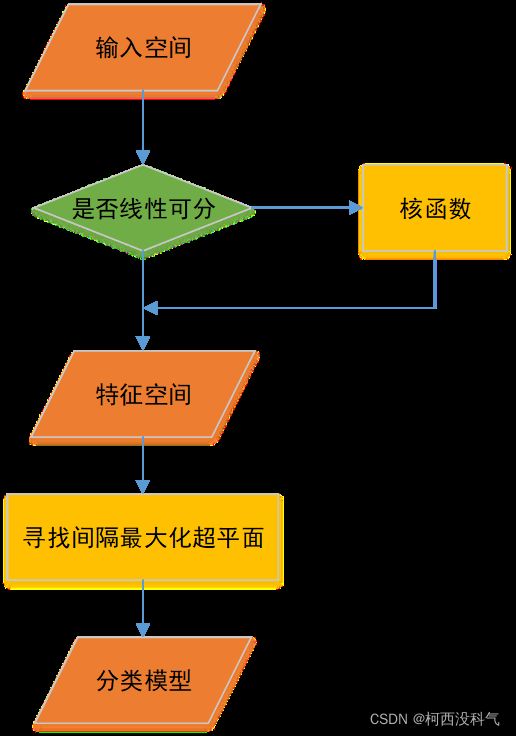
支持向量机(support vector machines)是一种二分类模型,是定义在特征空间上的间隔最大的线性分类器。它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题(convex quadratic programming)来求解,可等价于正则化的合页损失函数最小化问题。SVM算法流程如图1所示:
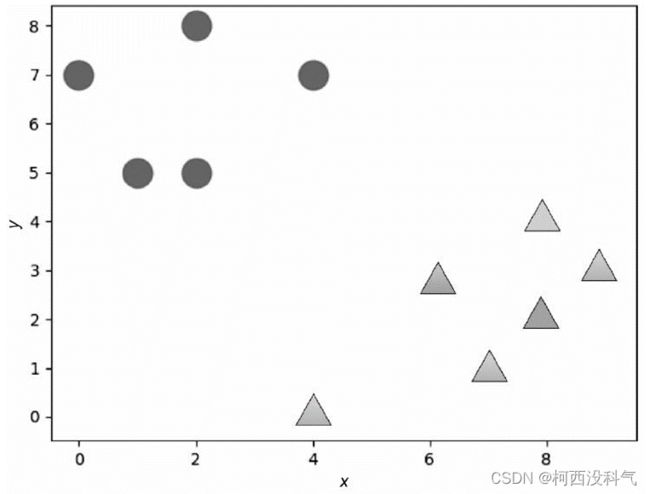
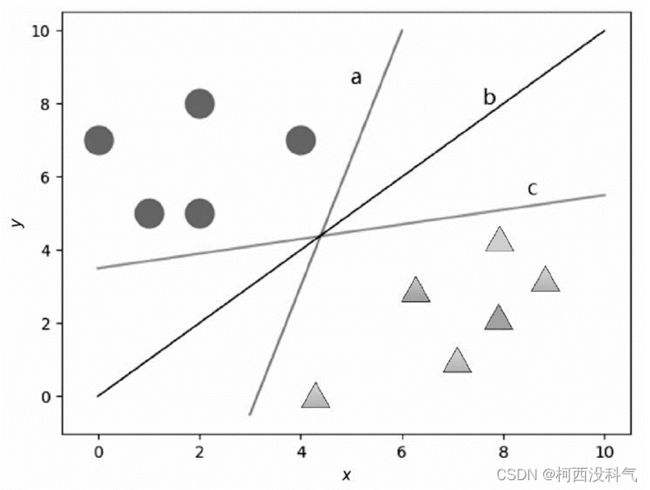
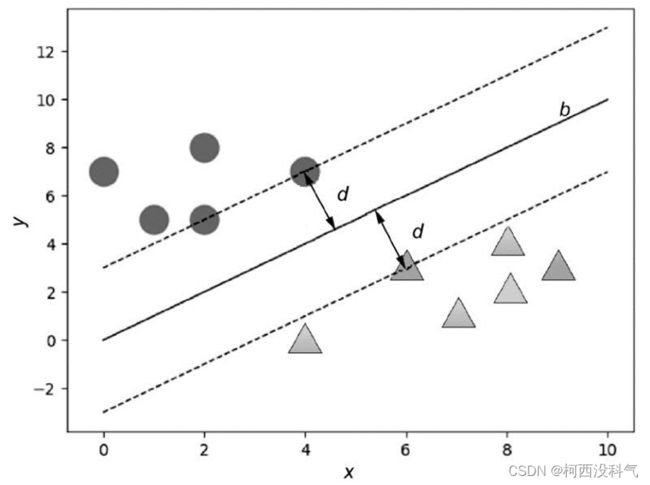
SVM的基本思想是:给定训练样本,支持向量机建立一个超平面作为决策曲面,使得正例和反例的隔离边界最大化。假设有图2 的两类数据,可以找到很多线将图的两类数据分割开,如图3 所示。而支持向量机要做的就是从这些分割线(平面)中寻找一个最优的。最优分割给人的直观感受就是在原有样本的基础上再增加分类样本而不影响原有的分类结果。从图4 不难看出,处在两类样本中间的分割线 b 能达到上述效果,这时两类数据的边缘到分割线 b 的距离是最大的。虚线穿过两个数据边缘的点被称为支持向量(support vector)。
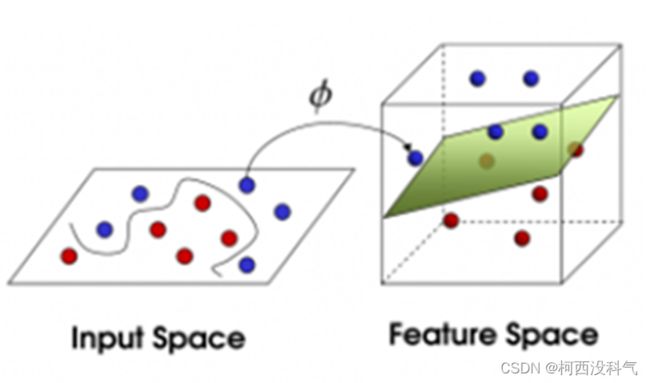
如果这些数据并不是在一个二维平面内,而是分布在在高维度的几何空间中,如果仍然需要将这两类样本数据分开,这时就需要一个曲面(而不是分割线),而且同样需要这个曲面仍然满足跟任意两类数据的间距的最大化,如图5 所示。需要找到的这个曲面,就是一个最优超平面。对于这样的线性不可分问题,需要将样本从原始空间映射到更高维的特征空间,在高维空间将非线性的问题转化为线性可分的问题。
2. 数据集介绍
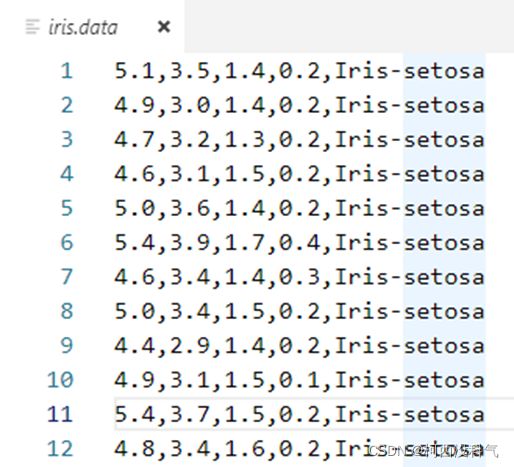
本算法中采用的数据集(Iris.data)直接从UCI的官网下载,这些数据共有5列,150行。前 4 列为鸢尾花的属性,分别为:花萼长度,花萼宽度,花瓣长度,花瓣宽度。第5列为鸢尾花的类别,分别有三种类别:Iris-setosa, Iris-versicolor, Iris-virginica,部分数据如图6 所示。由于在分类中类别标签为数字量,所以应将 Iris.data 中的第 5 列的类别从字符串的类型转换为数值类型。定义的转换函数为:可实现将类别 Iris-setosa, Iris-versicolor, Iris-virginica 映射成 0,1,2。
3. 算法流程
算法的准备工作包括准备数据集和导入模块,实现步骤包括:读取数据、划分数据与标签、训练svc分类器、计算svc分类器的准确率和绘制图形。算法流程如图7 所示。
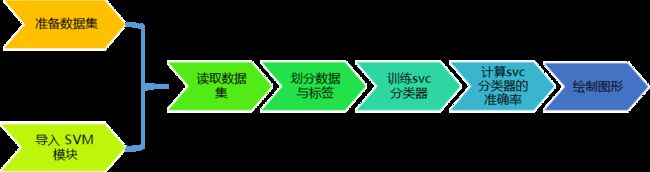
图8 显示了算法运行后的划分结果:
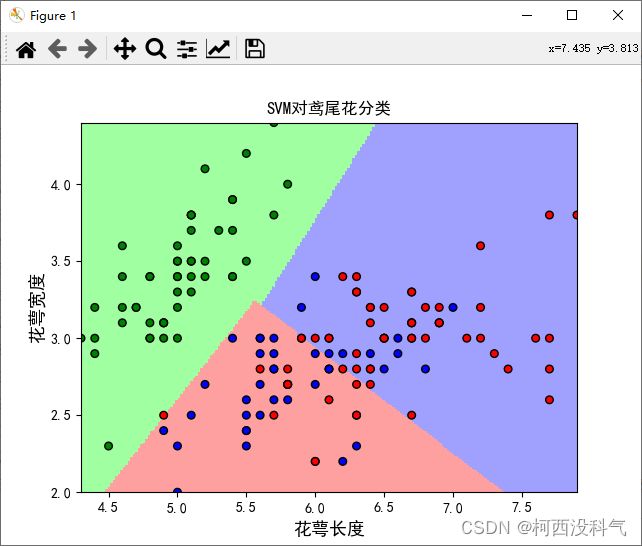
图9 显示了算法训练后的准确率。

4. 实现代码
import numpy as np
from matplotlib import colors
from sklearn import svm
from sklearn.svm import SVC
from sklearn import model_selection
import matplotlib.pyplot as plt
import matplotlib as mpl
def load_data():
# 导入数据
data = np.loadtxt('./iris.data', dtype=float, delimiter=',', converters={4: iris_type})
return data
def iris_type(s):
# 数据转为整型,数据集标签类别由string转为int
it = {b'Iris-setosa': 0, b'Iris-versicolor': 1, b'Iris-virginica': 2}
return it[s]
# 定义分类器
def classifier():
clf = svm.SVC(C=0.5, # 误差项惩罚系数
kernel='linear', # 线性核 kernel="rbf":高斯核
decision_function_shape='ovr') # 决策函数
return clf
def train(clf, x_train, y_train):
# x_train:训练数据集
# y_train:训练数据集标签
# 训练开始
# 同flnumpy.ravelatten将矩阵拉平
clf.fit(x_train, y_train.ravel(), sample_weight=None)
def show_accuracy(a, b, tip):
acc = a.ravel() == b.ravel()
print('%s Accuracy:%.3f' % (tip, np.mean(acc)))
def print_accuracy(clf, x_train, y_train, x_test, y_test):
show_accuracy(clf.predict(x_train), y_train, 'traing data')
show_accuracy(clf.predict(x_test), y_test, 'testing data')
def draw(clf, x):
iris_feature = '花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'
x1_min, x1_max = x[:, 0].min(), x[:, 0].max() # 第0列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max() # 第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j] # 生成网格采样点
grid_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点
grid_hat = clf.predict(grid_test) # 预测分类值 得到【0,0.。。。2,2,2】
grid_hat = grid_hat.reshape(x1.shape) # reshape grid_hat和x1形状一致
# 指定默认的字体
mpl.rcParams['font.sans-serif'] = ['SimHei']
# 设置颜色
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light) # 预测值的显示
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=30, cmap=cm_dark) # 样本点
plt.scatter(x_test[:, 0], x_test[:, 1], s=30, facecolor='none', zorder=10) # 测试点
plt.xlabel(iris_feature[0], fontsize=13)
plt.ylabel(iris_feature[1], fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title("SVM对鸢尾花分类")
plt.show()
# 训练四个特征:
data = load_data()
x, y = np.split(data, (4,), axis=1) # x为前四列,y为第五列,x为训练数据,y为数据标签
# x_train,x_test,y_train,y_test = 训练数据,测试数据,训练数据标签,测试数据标签
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, random_state=1,
test_size=0.3) # 数据集划分成70%30%测试集
clf = classifier() # 声明svm分类器对象
train(clf, x_train, y_train) # 启动分类器进行模型训练
print_accuracy(clf, x_train, y_train, x_test, y_test)
# 训练两个特征(用于画图展示)
data = load_data()
x, y = np.split(data, (4,), axis=1) # x为前四列,y为第五列,x为训练数据,y为数据标签
x = x[:, :2] # 只要前两个特征,此时只训练前两个特征,用于画图
x_train, x_test, y_train, y_test = model_selection.train_test_split(
x, y, random_state=1, test_size=0.3)
clf = classifier()
train(clf, x_train, y_train)
print_accuracy(clf, x_train, y_train, x_test, y_test)
draw(clf, x)
dom_state=1, test_size=0.3)
clf = classifier()
train(clf, x_train, y_train)
print_accuracy(clf, x_train, y_train, x_test, y_test)
draw(clf, x)